Ausreißererkennung auf einem realen Datensatz

Dieses Beispiel veranschaulicht die Notwendigkeit einer robusten Kovarianzschätzung auf einem realen Datensatz. Es ist sowohl für die Ausreißererkennung als auch für ein besseres Verständnis der Datenstruktur nützlich.

Wir haben zwei Teilmengen von zwei Variablen aus dem Wine-Datensatz ausgewählt, um zu veranschaulichen, welche Art von Analyse mit verschiedenen Werkzeugen zur Ausreißererkennung durchgeführt werden kann. Zur Visualisierung arbeiten wir mit zweidimensionalen Beispielen, aber man sollte sich bewusst sein, dass die Dinge in hoher Dimension nicht so einfach sind, wie noch aufgezeigt werden wird.

In beiden unten stehenden Beispielen besteht das Hauptergebnis darin, dass die empirische Kovarianzschätzung als nicht-robuste Schätzung stark von der heterogenen Struktur der Beobachtungen beeinflusst wird. Obwohl die robuste Kovarianzschätzung in der Lage ist, sich auf den Hauptmodus der Datenverteilung zu konzentrieren, hält sie an der Annahme fest, dass die Daten Gauß-verteilt sein sollten, was zu einer verzerrten Schätzung der Datenstruktur führt, aber dennoch bis zu einem gewissen Grad genau ist. Die One-Class SVM nimmt keine parametrische Form der Datenverteilung an und kann daher die komplexe Form der Daten viel besser modellieren.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

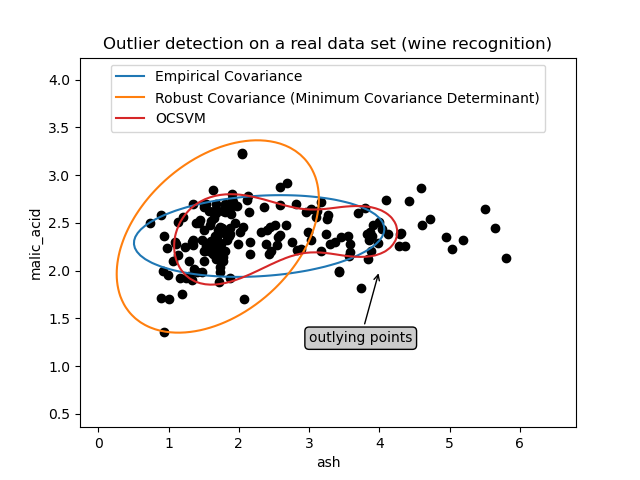
Erstes Beispiel

Das erste Beispiel veranschaulicht, wie der robuste Schätzer Minimum Covariance Determinant helfen kann, sich auf einen relevanten Cluster zu konzentrieren, wenn Ausreißerpunkte vorhanden sind. Hier wird die empirische Kovarianzschätzung durch Punkte außerhalb des Hauptclusters verzerrt. Natürlich hätten einige Screening-Tools die Anwesenheit von zwei Clustern aufgezeigt (Support Vector Machines, Gaussian Mixture Models, univariate Ausreißererkennung, ...). Aber bei einem hochdimensionalen Beispiel hätten keine davon so einfach angewendet werden können.

from sklearn.covariance import EllipticEnvelope
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.svm import OneClassSVM

estimators = {
    "Empirical Covariance": EllipticEnvelope(support_fraction=1.0, contamination=0.25),
    "Robust Covariance (Minimum Covariance Determinant)": EllipticEnvelope(
        contamination=0.25
    ),
    "OCSVM": OneClassSVM(nu=0.25, gamma=0.35),
}

import matplotlib.lines as mlines
import matplotlib.pyplot as plt

from sklearn.datasets import load_wine

X = load_wine()["data"][:, [1, 2]]  # two clusters

fig, ax = plt.subplots()
colors = ["tab:blue", "tab:orange", "tab:red"]
# Learn a frontier for outlier detection with several classifiers
legend_lines = []
for color, (name, estimator) in zip(colors, estimators.items()):
    estimator.fit(X)
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="decision_function",
        plot_method="contour",
        levels=[0],
        colors=color,
        ax=ax,
    )
    legend_lines.append(mlines.Line2D([], [], color=color, label=name))


ax.scatter(X[:, 0], X[:, 1], color="black")
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
ax.annotate(
    "outlying points",
    xy=(4, 2),
    xycoords="data",
    textcoords="data",
    xytext=(3, 1.25),
    bbox=bbox_args,
    arrowprops=arrow_args,
)
ax.legend(handles=legend_lines, loc="upper center")
_ = ax.set(
    xlabel="ash",
    ylabel="malic_acid",
    title="Outlier detection on a real data set (wine recognition)",
)

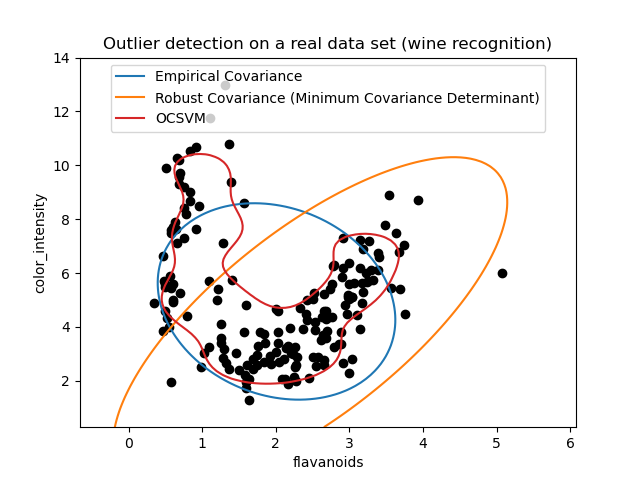
Zweites Beispiel

Das zweite Beispiel zeigt die Fähigkeit des robusten Kovarianzschätzers Minimum Covariance Determinant, sich auf den Hauptmodus der Datenverteilung zu konzentrieren: Die Position scheint gut geschätzt zu sein, obwohl die Kovarianz aufgrund der bananenförmigen Verteilung schwer zu schätzen ist. Jedenfalls können wir einige Ausreißerbeobachtungen loswerden. Die One-Class SVM ist in der Lage, die reale Datenstruktur zu erfassen, aber die Schwierigkeit besteht darin, ihren Kernel-Bandbreitenparameter so anzupassen, dass ein guter Kompromiss zwischen der Form der Datenstreuungsmatrix und dem Risiko einer Überanpassung der Daten erzielt wird.

X = load_wine()["data"][:, [6, 9]]  # "banana"-shaped

fig, ax = plt.subplots()
colors = ["tab:blue", "tab:orange", "tab:red"]
# Learn a frontier for outlier detection with several classifiers
legend_lines = []
for color, (name, estimator) in zip(colors, estimators.items()):
    estimator.fit(X)
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="decision_function",
        plot_method="contour",
        levels=[0],
        colors=color,
        ax=ax,
    )
    legend_lines.append(mlines.Line2D([], [], color=color, label=name))


ax.scatter(X[:, 0], X[:, 1], color="black")
ax.legend(handles=legend_lines, loc="upper center")
ax.set(
    xlabel="flavanoids",
    ylabel="color_intensity",
    title="Outlier detection on a real data set (wine recognition)",
)

plt.show()

Verwandte Beispiele

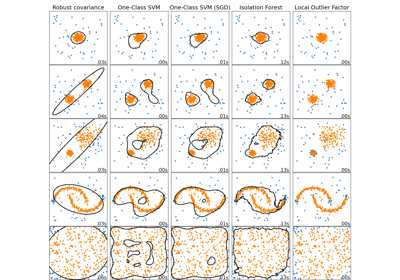
Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen

Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen

Ausreißererkennung mit Local Outlier Factor (LOF)

Ausreißererkennung mit Local Outlier Factor (LOF)

Robuste vs. Empirische Kovarianzschätzung

Robuste vs. Empirische Kovarianzschätzung

Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid

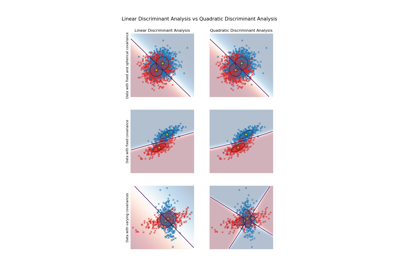
Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid