Modellauswahl mit probabilistischem PCA und Faktoranalyse (FA)

Probabilistische PCA und Faktoranalyse sind probabilistische Modelle. Die Konsequenz ist, dass die Likelihood neuer Daten für die Modellauswahl und die Kovarianzschätzung verwendet werden kann. Hier vergleichen wir PCA und FA mit Kreuzvalidierung auf niedrigrangigen Daten, die mit homoskedastischem Rauschen (Rauschvarianz ist für jedes Merkmal gleich) oder heteroskedastischem Rauschen (Rauschvarianz ist für jedes Merkmal unterschiedlich) verunreinigt sind. In einem zweiten Schritt vergleichen wir die Modell-Likelihood mit den Likelihoods, die von Shrinkage-Kovarianzschätzern erhalten wurden.

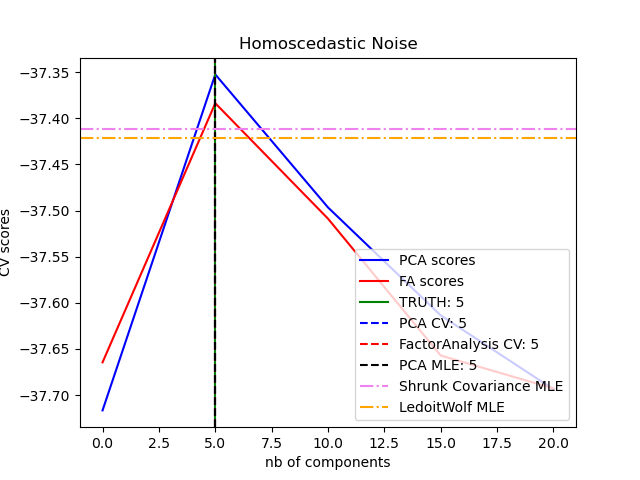
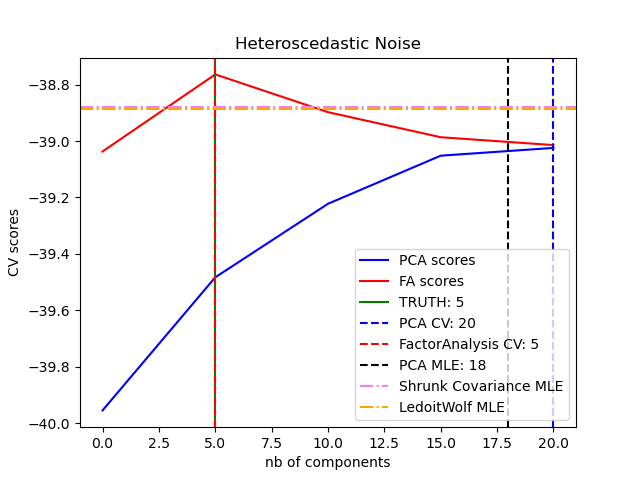
Man kann beobachten, dass bei homoskedastischem Rauschen sowohl FA als auch PCA die Größe des niedrigrangigen Unterraums erfolgreich wiederherstellen. Die Likelihood mit PCA ist in diesem Fall höher als bei FA. PCA scheitert jedoch und überschätzt den Rang, wenn heteroskedastisches Rauschen vorhanden ist. Unter geeigneten Umständen (Wahl der Anzahl der Komponenten) ist die zurückgehaltene Datenmenge für niedrigrangige Modelle wahrscheinlicher als für Shrinkage-Modelle.

Die automatische Schätzung aus "Automatic Choice of Dimensionality for PCA. NIPS 2000: 598-604" von Thomas P. Minka wird ebenfalls verglichen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Erstellen der Daten

import numpy as np
from scipy import linalg

n_samples, n_features, rank = 500, 25, 5
sigma = 1.0
rng = np.random.RandomState(42)
U, _, _ = linalg.svd(rng.randn(n_features, n_features))
X = np.dot(rng.randn(n_samples, rank), U[:, :rank].T)

# Adding homoscedastic noise
X_homo = X + sigma * rng.randn(n_samples, n_features)

# Adding heteroscedastic noise
sigmas = sigma * rng.rand(n_features) + sigma / 2.0
X_hetero = X + rng.randn(n_samples, n_features) * sigmas

Anpassen der Modelle

import matplotlib.pyplot as plt

from sklearn.covariance import LedoitWolf, ShrunkCovariance
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn.model_selection import GridSearchCV, cross_val_score

n_components = np.arange(0, n_features, 5)  # options for n_components


def compute_scores(X):
    pca = PCA(svd_solver="full")
    fa = FactorAnalysis()

    pca_scores, fa_scores = [], []
    for n in n_components:
        pca.n_components = n
        fa.n_components = n
        pca_scores.append(np.mean(cross_val_score(pca, X)))
        fa_scores.append(np.mean(cross_val_score(fa, X)))

    return pca_scores, fa_scores


def shrunk_cov_score(X):
    shrinkages = np.logspace(-2, 0, 30)
    cv = GridSearchCV(ShrunkCovariance(), {"shrinkage": shrinkages})
    return np.mean(cross_val_score(cv.fit(X).best_estimator_, X))


def lw_score(X):
    return np.mean(cross_val_score(LedoitWolf(), X))


for X, title in [(X_homo, "Homoscedastic Noise"), (X_hetero, "Heteroscedastic Noise")]:
    pca_scores, fa_scores = compute_scores(X)
    n_components_pca = n_components[np.argmax(pca_scores)]
    n_components_fa = n_components[np.argmax(fa_scores)]

    pca = PCA(svd_solver="full", n_components="mle")
    pca.fit(X)
    n_components_pca_mle = pca.n_components_

    print("best n_components by PCA CV = %d" % n_components_pca)
    print("best n_components by FactorAnalysis CV = %d" % n_components_fa)
    print("best n_components by PCA MLE = %d" % n_components_pca_mle)

    plt.figure()
    plt.plot(n_components, pca_scores, "b", label="PCA scores")
    plt.plot(n_components, fa_scores, "r", label="FA scores")
    plt.axvline(rank, color="g", label="TRUTH: %d" % rank, linestyle="-")
    plt.axvline(
        n_components_pca,
        color="b",
        label="PCA CV: %d" % n_components_pca,
        linestyle="--",
    )
    plt.axvline(
        n_components_fa,
        color="r",
        label="FactorAnalysis CV: %d" % n_components_fa,
        linestyle="--",
    )
    plt.axvline(
        n_components_pca_mle,
        color="k",
        label="PCA MLE: %d" % n_components_pca_mle,
        linestyle="--",
    )

    # compare with other covariance estimators
    plt.axhline(
        shrunk_cov_score(X),
        color="violet",
        label="Shrunk Covariance MLE",
        linestyle="-.",
    )
    plt.axhline(
        lw_score(X),
        color="orange",
        label="LedoitWolf MLE" % n_components_pca_mle,
        linestyle="-.",
    )

    plt.xlabel("nb of components")
    plt.ylabel("CV scores")
    plt.legend(loc="lower right")
    plt.title(title)

plt.show()

• 
• 

best n_components by PCA CV = 5
best n_components by FactorAnalysis CV = 5
best n_components by PCA MLE = 5
best n_components by PCA CV = 20
best n_components by FactorAnalysis CV = 5
best n_components by PCA MLE = 18

Verwandte Beispiele

Faktorenanalyse (mit Rotation) zur Visualisierung von Mustern

Faktorenanalyse (mit Rotation) zur Visualisierung von Mustern

Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood

Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood

Robuste Kovarianzschätzung und Relevanz von Mahalanobis-Distanzen

Robuste Kovarianzschätzung und Relevanz von Mahalanobis-Distanzen

Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation