Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Spiel-Datensätzen

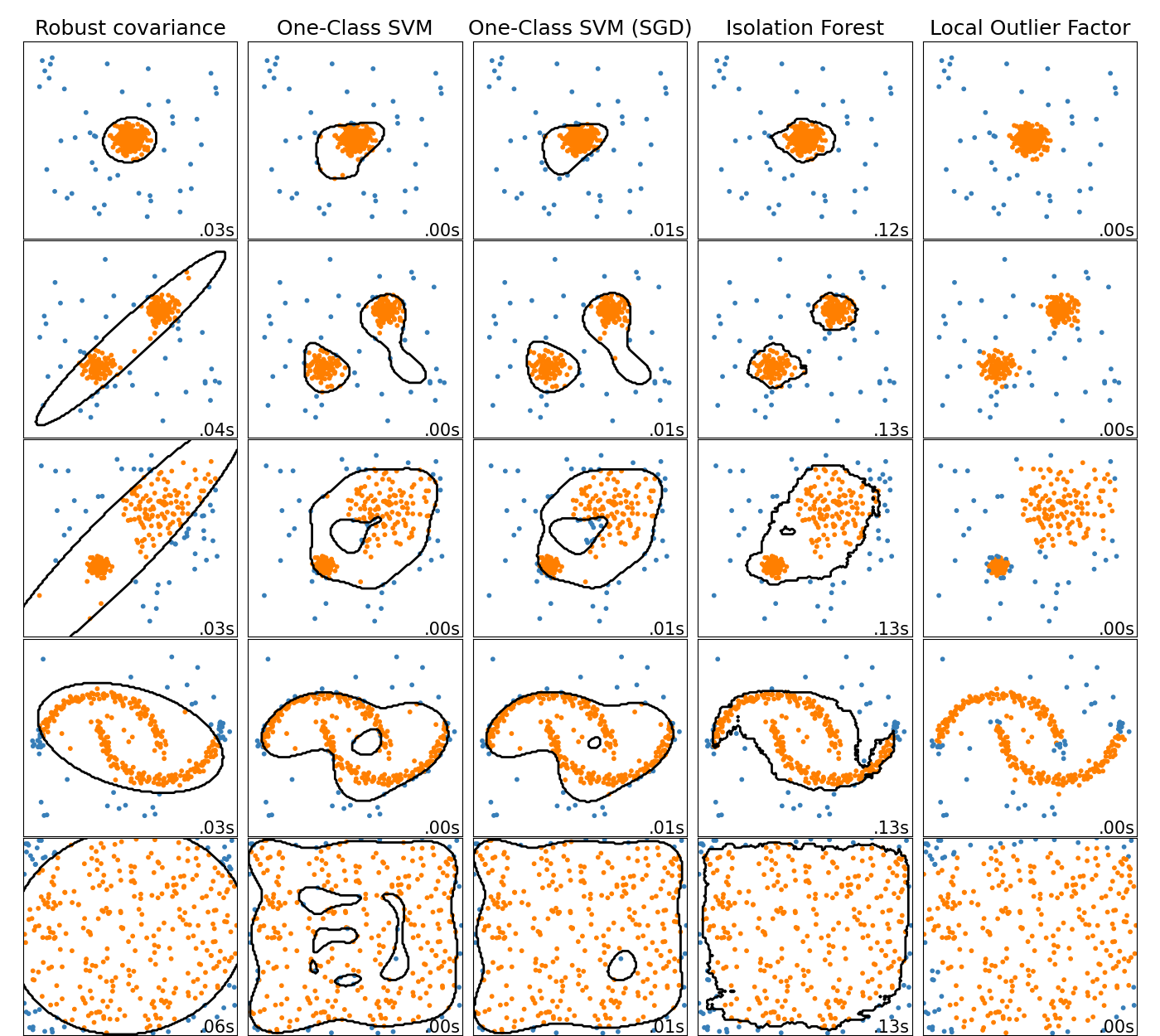
Dieses Beispiel zeigt die Eigenschaften verschiedener Anomalieerkennungsalgorithmen auf 2D-Datensätzen. Die Datensätze enthalten eine oder zwei Modi (Regionen hoher Dichte), um die Fähigkeit der Algorithmen zu demonstrieren, mit multimodalen Daten umzugehen.

Für jeden Datensatz werden 15% der Stichproben als zufälliges gleichmäßiges Rauschen generiert. Dieser Anteil ist der Wert, der dem Parameter `nu` von `OneClassSVM` und dem Parameter `contamination` der anderen Ausreißererkennungsalgorithmen gegeben wird. Entscheidungsgrenzen zwischen Inliern und Ausreißern werden schwarz angezeigt, mit Ausnahme von Local Outlier Factor (LOF), da es keine `predict`-Methode hat, die auf neue Daten angewendet werden kann, wenn es zur Ausreißererkennung verwendet wird.

Der OneClassSVM ist dafür bekannt, empfindlich auf Ausreißer zu reagieren und schneidet daher bei der Ausreißererkennung nicht sehr gut ab. Dieser Schätzer ist am besten für die Neuheitserkennung geeignet, wenn der Trainingsdatensatz nicht durch Ausreißer verunreinigt ist. Dennoch ist die Ausreißererkennung in hoher Dimension oder ohne Annahmen über die Verteilung der Inlier-Daten sehr herausfordernd, und eine One-Class-SVM kann in diesen Situationen je nach Wert ihrer Hyperparameter nützliche Ergebnisse liefern.

Der sklearn.linear_model.SGDOneClassSVM ist eine Implementierung der One-Class-SVM basierend auf stochastischem Gradientenabstieg (SGD). In Kombination mit der Kernel-Approximation kann dieser Schätzer verwendet werden, um die Lösung einer kernelisierten sklearn.svm.OneClassSVM zu approximieren. Wir stellen fest, dass, obwohl nicht identisch, die Entscheidungsgrenzen des sklearn.linear_model.SGDOneClassSVM und die des sklearn.svm.OneClassSVM sehr ähnlich sind. Der Hauptvorteil der Verwendung von sklearn.linear_model.SGDOneClassSVM ist, dass er linear mit der Anzahl der Stichproben skaliert.

sklearn.covariance.EllipticEnvelope nimmt an, dass die Daten Gaußsch verteilt sind und lernt eine Ellipse. Daher verschlechtert er sich, wenn die Daten nicht unimodal sind. Beachten Sie jedoch, dass dieser Schätzer robust gegenüber Ausreißern ist.

IsolationForest und LocalOutlierFactor scheinen für multimodale Datensätze vernünftige Ergebnisse zu liefern. Der Vorteil von LocalOutlierFactor gegenüber den anderen Schätzern zeigt sich für den dritten Datensatz, bei dem die beiden Modi unterschiedliche Dichten aufweisen. Dieser Vorteil erklärt sich durch den lokalen Aspekt von LOF, was bedeutet, dass er die Anomalie-Bewertung einer Stichprobe nur mit den Bewertungen ihrer Nachbarn vergleicht.

Schließlich ist es für den letzten Datensatz schwer zu sagen, ob eine Stichprobe abnormaler ist als eine andere, da sie gleichmäßig in einem Hyperwürfel verteilt sind. Mit Ausnahme von OneClassSVM, das leicht überanpasst, bieten alle Schätzer für diese Situation anständige Lösungen. In einem solchen Fall wäre es ratsam, die Anomalie-Bewertungen der Stichproben genauer zu betrachten, da ein guter Schätzer allen Stichproben ähnliche Bewertungen zuweisen sollte.

Obwohl diese Beispiele einige Intuition über die Algorithmen vermitteln, gilt diese Intuition möglicherweise nicht für Daten mit sehr hoher Dimensionalität.

Schließlich ist zu beachten, dass die Parameter der Modelle hier von Hand gewählt wurden, aber in der Praxis angepasst werden müssen. In Abwesenheit von gelabelten Daten ist das Problem vollständig unüberwacht, so dass die Modellauswahl eine Herausforderung darstellen kann.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline

matplotlib.rcParams["contour.negative_linestyle"] = "solid"

# Example settings
n_samples = 300
outliers_fraction = 0.15
n_outliers = int(outliers_fraction * n_samples)
n_inliers = n_samples - n_outliers

# define outlier/anomaly detection methods to be compared.
# the SGDOneClassSVM must be used in a pipeline with a kernel approximation
# to give similar results to the OneClassSVM
anomaly_algorithms = [
    (
        "Robust covariance",
        EllipticEnvelope(contamination=outliers_fraction, random_state=42),
    ),
    ("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
    (
        "One-Class SVM (SGD)",
        make_pipeline(
            Nystroem(gamma=0.1, random_state=42, n_components=150),
            SGDOneClassSVM(
                nu=outliers_fraction,
                shuffle=True,
                fit_intercept=True,
                random_state=42,
                tol=1e-6,
            ),
        ),
    ),
    (
        "Isolation Forest",
        IsolationForest(contamination=outliers_fraction, random_state=42),
    ),
    (
        "Local Outlier Factor",
        LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction),
    ),
]

# Define datasets
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
    make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
    4.0
    * (
        make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0]
        - np.array([0.5, 0.25])
    ),
    14.0 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5),
]

# Compare given classifiers under given settings
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))

plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(
    left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)

plot_num = 1
rng = np.random.RandomState(42)

for i_dataset, X in enumerate(datasets):
    # Add outliers
    X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)

    for name, algorithm in anomaly_algorithms:
        t0 = time.time()
        algorithm.fit(X)
        t1 = time.time()
        plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
        if i_dataset == 0:
            plt.title(name, size=18)

        # fit the data and tag outliers
        if name == "Local Outlier Factor":
            y_pred = algorithm.fit_predict(X)
        else:
            y_pred = algorithm.fit(X).predict(X)

        # plot the levels lines and the points
        if name != "Local Outlier Factor":  # LOF does not implement predict
            Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
            Z = Z.reshape(xx.shape)
            plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")

        colors = np.array(["#377eb8", "#ff7f00"])
        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])

        plt.xlim(-7, 7)
        plt.ylim(-7, 7)
        plt.xticks(())
        plt.yticks(())
        plt.text(
            0.99,
            0.01,
            ("%.2fs" % (t1 - t0)).lstrip("0"),
            transform=plt.gca().transAxes,
            size=15,
            horizontalalignment="right",
        )
        plot_num += 1

plt.show()

Verwandte Beispiele

Ausreißererkennung mit Local Outlier Factor (LOF)

Ausreißererkennung mit Local Outlier Factor (LOF)

Neuartigkeitserkennung mit Local Outlier Factor (LOF)

Neuartigkeitserkennung mit Local Outlier Factor (LOF)

Ausreißererkennung auf einem realen Datensatz

Ausreißererkennung auf einem realen Datensatz

One-Class SVM vs. One-Class SVM mittels Stochastic Gradient Descent

One-Class SVM vs. One-Class SVM mittels Stochastic Gradient Descent