RBF SVM Parameter

Dieses Beispiel veranschaulicht die Auswirkung der Parameter gamma und C des Radial Basis Function (RBF) Kernel SVM.

Intuitiv definiert der gamma-Parameter, wie weit der Einfluss eines einzelnen Trainingsbeispiels reicht, wobei niedrige Werte „weit“ und hohe Werte „nah“ bedeuten. Die gamma-Parameter können als Kehrwert des Einflussradius von Stichproben betrachtet werden, die vom Modell als Stützvektoren ausgewählt werden.

Der C-Parameter tauscht die korrekte Klassifizierung von Trainingsbeispielen gegen die Maximierung des Abstands der Entscheidungsfunktion. Bei größeren Werten von C wird ein kleinerer Abstand akzeptiert, wenn die Entscheidungsfunktion alle Trainingspunkte korrekt klassifiziert. Ein niedrigeres C fördert einen größeren Abstand und damit eine einfachere Entscheidungsfunktion, allerdings auf Kosten der Trainingsgenauigkeit. Mit anderen Worten: C verhält sich wie ein Regularisierungsparameter im SVM.

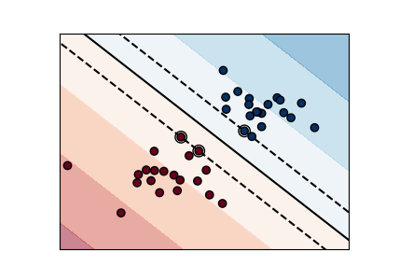
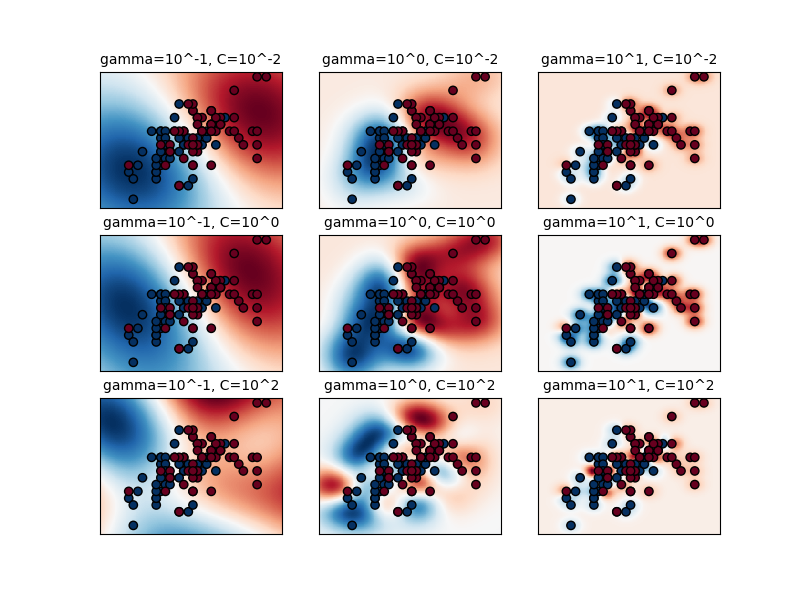
Die erste Abbildung ist eine Visualisierung der Entscheidungsfunktion für eine Vielzahl von Parameterwerten bei einem vereinfachten Klassifizierungsproblem mit nur 2 Eingabemerkmalen und 2 möglichen Zielklassen (binäre Klassifizierung). Beachten Sie, dass diese Art der Darstellung für Probleme mit mehr Merkmalen oder Zielklassen nicht möglich ist.

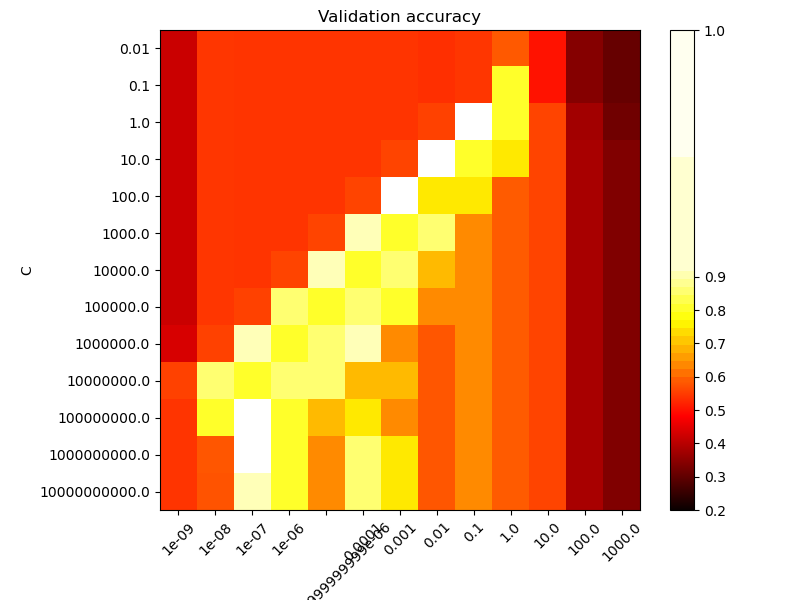
Die zweite Abbildung ist eine Heatmap der Kreuzvalidierungsgenauigkeit des Klassifikators als Funktion von C und gamma. Für dieses Beispiel untersuchen wir zu Illustrationszwecken ein relativ großes Gitter. In der Praxis ist ein logarithmischer Gitter von \(10^{-3}\) bis \(10^3\) normalerweise ausreichend. Wenn sich die besten Parameter an den Grenzen des Gitters befinden, kann dies in einem nachfolgenden Suchlauf in diese Richtung erweitert werden.

Beachten Sie, dass die Heatmap-Abbildung eine spezielle Farbleiste mit einem Mittelpunkt nahe den Wertebereichen der am besten funktionierenden Modelle aufweist, um sie auf einen Blick leicht unterscheiden zu können.

Das Verhalten des Modells ist sehr empfindlich gegenüber dem gamma-Parameter. Wenn gamma zu groß ist, umfasst der Radius des Einflussbereichs der Stützvektoren nur den Stützvektor selbst, und keine Regularisierung mit C kann Überanpassung verhindern.

Wenn gamma sehr klein ist, ist das Modell zu eingeschränkt und kann die Komplexität oder „Form“ der Daten nicht erfassen. Der Einflussbereich jedes ausgewählten Stützvektors würde den gesamten Trainingsdatensatz umfassen. Das resultierende Modell verhält sich ähnlich wie ein lineares Modell mit einer Reihe von Hyper-Ebenen, die die Zentren hoher Dichte von jeweils zwei Klassen trennen.

Für Zwischenwerte sehen wir auf der zweiten Abbildung, dass gute Modelle auf einer Diagonale von C und gamma gefunden werden können. Glatte Modelle (niedrigere gamma-Werte) können durch Erhöhung der Bedeutung der korrekten Klassifizierung jedes Punktes (höhere C-Werte) komplexer gemacht werden, daher die Diagonale gut funktionierender Modelle.

Schließlich kann man auch beobachten, dass wir bei einigen Zwischenwerten von gamma gleich gut funktionierende Modelle erhalten, wenn C sehr groß wird. Dies deutet darauf hin, dass sich die Menge der Stützvektoren nicht mehr ändert. Der Radius des RBF-Kernels allein wirkt als gute strukturelle Regularisierung. Eine weitere Erhöhung von C hilft nicht, wahrscheinlich weil keine Trainingspunkte mehr verletzt werden (innerhalb des Randes oder falsch klassifiziert werden) oder zumindest keine bessere Lösung gefunden werden kann. Da die Punktzahlen gleich sind, kann es sinnvoll sein, die kleineren C-Werte zu verwenden, da sehr hohe C-Werte typischerweise die Trainingszeit erhöhen.

Andererseits führen niedrigere C-Werte im Allgemeinen zu mehr Stützvektoren, was die Vorhersagezeit erhöhen kann. Daher beinhaltet die Senkung des C-Werts einen Kompromiss zwischen Trainingszeit und Vorhersagezeit.

Wir sollten auch beachten, dass kleine Unterschiede in den Punktzahlen auf die zufälligen Aufteilungen des Kreuzvalidierungsverfahrens zurückzuführen sind. Diese Scheinvankommen können durch Erhöhung der Anzahl der CV-Iterationen n_splits auf Kosten der Rechenzeit geglättet werden. Die Erhöhung der Anzahl der Schritte in C_range und gamma_range erhöht die Auflösung der Hyperparameter-Heatmap.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Hilfsklasse zum Verschieben des Mittelpunkts einer Colormap um die interessanten Werte herum.

import numpy as np
from matplotlib.colors import Normalize


class MidpointNormalize(Normalize):
    def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
        self.midpoint = midpoint
        Normalize.__init__(self, vmin, vmax, clip)

    def __call__(self, value, clip=None):
        x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
        return np.ma.masked_array(np.interp(value, x, y))

Datensatz laden und vorbereiten

Datensatz für Grid Search

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

Datensatz zur Visualisierung der Entscheidungsfunktion: Wir behalten nur die ersten beiden Merkmale in X und unterabsample den Datensatz, um nur 2 Klassen zu behalten und ihn zu einem binären Klassifizierungsproblem zu machen.

X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1

Es ist normalerweise eine gute Idee, die Daten für das SVM-Training zu skalieren. Wir schummeln hier ein wenig, indem wir alle Daten skalieren, anstatt die Transformation auf dem Trainingsdatensatz anzupassen und sie nur auf dem Testdatensatz anzuwenden.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)

Klassifikatoren trainieren

Für eine anfängliche Suche ist ein logarithmischer Gitter mit Basis 10 oft hilfreich. Mit einer Basis von 2 kann eine feinere Abstimmung erreicht werden, allerdings zu deutlich höheren Kosten.

from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
from sklearn.svm import SVC

C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

print(
    "The best parameters are %s with a score of %0.2f"
    % (grid.best_params_, grid.best_score_)
)

The best parameters are {'C': np.float64(1.0), 'gamma': np.float64(0.1)} with a score of 0.97

Nun müssen wir einen Klassifikator für alle Parameter in der 2D-Version anpassen (wir verwenden hier eine kleinere Parametermenge, da das Training eine Weile dauert).

C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
    for gamma in gamma_2d_range:
        clf = SVC(C=C, gamma=gamma)
        clf.fit(X_2d, y_2d)
        classifiers.append((C, gamma, clf))

Visualisierung

Visualisierung der Parameterwirkungen zeichnen

import matplotlib.pyplot as plt

plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for k, (C, gamma, clf) in enumerate(classifiers):
    # evaluate decision function in a grid
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # visualize decision function for these parameters
    plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
    plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)), size="medium")

    # visualize parameter's effect on decision function
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
    plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r, edgecolors="k")
    plt.xticks(())
    plt.yticks(())
    plt.axis("tight")

scores = grid.cv_results_["mean_test_score"].reshape(len(C_range), len(gamma_range))

Heatmap der Validierungsgenauigkeit als Funktion von Gamma und C zeichnen

Die Punktzahlen sind als Farben mit der Hot-Colormap kodiert, die von dunkelrot bis leuchtend gelb variiert. Da die interessantesten Punktzahlen alle im Bereich von 0,92 bis 0,97 liegen, verwenden wir einen benutzerdefinierten Normalisierer, um den Mittelpunkt auf 0,92 zu setzen, damit es einfacher ist, die kleinen Variationen der Punktwerte im interessanten Bereich zu visualisieren, ohne alle niedrigen Punktwerte brutal auf dieselbe Farbe zu reduzieren.

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=0.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(
    scores,
    interpolation="nearest",
    cmap=plt.cm.hot,
    norm=MidpointNormalize(vmin=0.2, midpoint=0.92),
)
plt.xlabel("gamma")
plt.ylabel("C")
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title("Validation accuracy")
plt.show()

Verwandte Beispiele

Klassifikationsgrenzen mit verschiedenen SVM-Kernen plotten

Klassifikationsgrenzen mit verschiedenen SVM-Kernen plotten

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

SVM-Randbeispiel

SVM-Randbeispiel

Illustration der Gauß-Prozess-Klassifikation (GPC) auf dem XOR-Datensatz

Illustration der Gauß-Prozess-Klassifikation (GPC) auf dem XOR-Datensatz