Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Auswirkungen der Transformation von Zielvariablen in Regressionsmodellen#
In diesem Beispiel geben wir einen Überblick über TransformedTargetRegressor. Wir verwenden zwei Beispiele, um den Nutzen der Transformation von Zielvariablen vor dem Erlernen eines linearen Regressionsmodells zu veranschaulichen. Das erste Beispiel verwendet synthetische Daten, während das zweite Beispiel auf dem Ames-Datensatz für Wohnimmobilien basiert.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Synthetisches Beispiel#
Ein synthetischer zufälliger Regressionsdatensatz wird generiert. Die Zielvariablen y werden modifiziert durch
Verschieben aller Zielvariablen, sodass alle Einträge nicht-negativ sind (durch Addition des Absolutwerts des kleinsten
y) undAnwenden einer Exponentialfunktion, um nicht-lineare Zielvariablen zu erhalten, die nicht durch ein einfaches lineares Modell angepasst werden können.
Daher werden eine logarithmische (np.log1p) und eine Exponentialfunktion (np.expm1) verwendet, um die Zielvariablen zu transformieren, bevor ein lineares Regressionsmodell trainiert und für Vorhersagen verwendet wird.
import numpy as np
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=10_000, noise=100, random_state=0)
y = np.expm1((y + abs(y.min())) / 200)
y_trans = np.log1p(y)
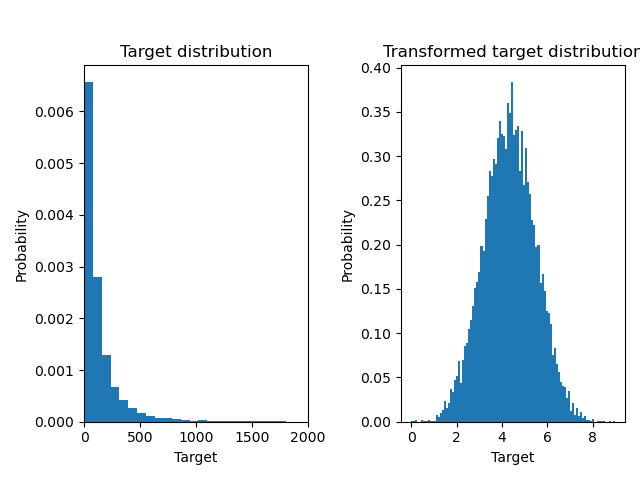
Unten plotten wir die Wahrscheinlichkeitsdichtefunktionen der Zielvariable vor und nach Anwendung der logarithmischen Funktionen.
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
f, (ax0, ax1) = plt.subplots(1, 2)
ax0.hist(y, bins=100, density=True)
ax0.set_xlim([0, 2000])
ax0.set_ylabel("Probability")
ax0.set_xlabel("Target")
ax0.set_title("Target distribution")
ax1.hist(y_trans, bins=100, density=True)
ax1.set_ylabel("Probability")
ax1.set_xlabel("Target")
ax1.set_title("Transformed target distribution")
f.suptitle("Synthetic data", y=1.05)
plt.tight_layout()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
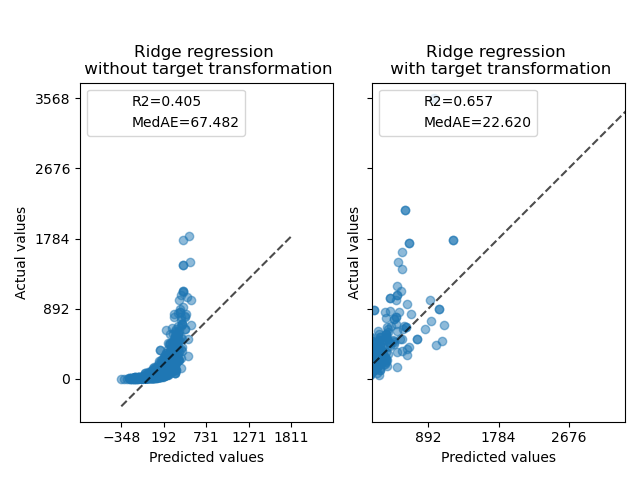
Zuerst wird ein lineares Modell auf die ursprünglichen Zielvariablen angewendet. Aufgrund der Nichtlinearität wird das trainierte Modell bei der Vorhersage nicht präzise sein. Anschließend wird eine logarithmische Funktion verwendet, um die Zielvariablen zu linearisieren, was eine bessere Vorhersage ermöglicht, selbst mit einem ähnlichen linearen Modell, wie durch den Median-Absolutfehler (MedAE) berichtet.
from sklearn.metrics import median_absolute_error, r2_score
def compute_score(y_true, y_pred):
return {
"R2": f"{r2_score(y_true, y_pred):.3f}",
"MedAE": f"{median_absolute_error(y_true, y_pred):.3f}",
}
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import RidgeCV
from sklearn.metrics import PredictionErrorDisplay
f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)
ridge_cv = RidgeCV().fit(X_train, y_train)
y_pred_ridge = ridge_cv.predict(X_test)
ridge_cv_with_trans_target = TransformedTargetRegressor(
regressor=RidgeCV(), func=np.log1p, inverse_func=np.expm1
).fit(X_train, y_train)
y_pred_ridge_with_trans_target = ridge_cv_with_trans_target.predict(X_test)
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge,
kind="actual_vs_predicted",
ax=ax0,
scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge_with_trans_target,
kind="actual_vs_predicted",
ax=ax1,
scatter_kwargs={"alpha": 0.5},
)
# Add the score in the legend of each axis
for ax, y_pred in zip([ax0, ax1], [y_pred_ridge, y_pred_ridge_with_trans_target]):
for name, score in compute_score(y_test, y_pred).items():
ax.plot([], [], " ", label=f"{name}={score}")
ax.legend(loc="upper left")
ax0.set_title("Ridge regression \n without target transformation")
ax1.set_title("Ridge regression \n with target transformation")
f.suptitle("Synthetic data", y=1.05)
plt.tight_layout()
Datensatz aus der realen Welt#
In ähnlicher Weise wird der Ames-Datensatz für Wohnimmobilien verwendet, um die Auswirkungen der Transformation von Zielvariablen vor dem Erlernen eines Modells zu zeigen. In diesem Beispiel ist die zu prognostizierende Zielvariable der Verkaufspreis jedes Hauses.
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import quantile_transform
ames = fetch_openml(name="house_prices", as_frame=True)
# Keep only numeric columns
X = ames.data.select_dtypes(np.number)
# Remove columns with NaN or Inf values
X = X.drop(columns=["LotFrontage", "GarageYrBlt", "MasVnrArea"])
# Let the price be in k$
y = ames.target / 1000
y_trans = quantile_transform(
y.to_frame(), n_quantiles=900, output_distribution="normal", copy=True
).squeeze()
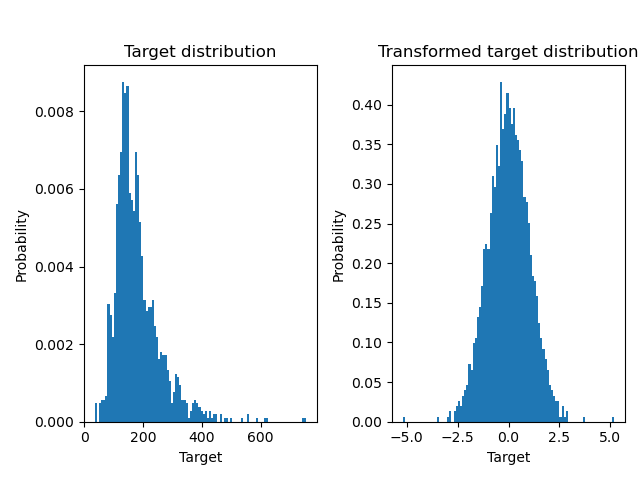
Ein QuantileTransformer wird verwendet, um die Zielvariablenverteilung zu normalisieren, bevor ein RidgeCV-Modell angewendet wird.
f, (ax0, ax1) = plt.subplots(1, 2)
ax0.hist(y, bins=100, density=True)
ax0.set_ylabel("Probability")
ax0.set_xlabel("Target")
ax0.set_title("Target distribution")
ax1.hist(y_trans, bins=100, density=True)
ax1.set_ylabel("Probability")
ax1.set_xlabel("Target")
ax1.set_title("Transformed target distribution")
f.suptitle("Ames housing data: selling price", y=1.05)
plt.tight_layout()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
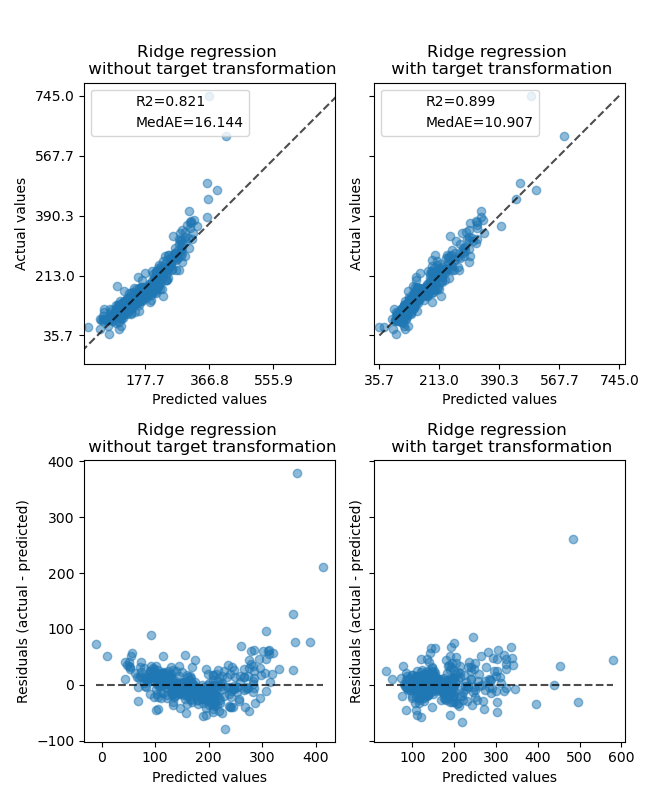
Der Effekt des Transformers ist auf dem synthetischen Datensatz schwächer. Die Transformation führt jedoch zu einer Erhöhung des \(R^2\) und einer starken Verringerung des MedAE. Das Residuen-Diagramm (vorhergesagte Zielvariable - tatsächliche Zielvariable vs. vorhergesagte Zielvariable) ohne Zieltransformation weist eine gekrümmte "umgekehrte Lächeln"-Form auf, da die Residuenwerte je nach Wert der vorhergesagten Zielvariable variieren. Mit Zieltransformation ist die Form linearer, was auf eine bessere Modell-Anpassung hindeutet.
from sklearn.preprocessing import QuantileTransformer
f, (ax0, ax1) = plt.subplots(2, 2, sharey="row", figsize=(6.5, 8))
ridge_cv = RidgeCV().fit(X_train, y_train)
y_pred_ridge = ridge_cv.predict(X_test)
ridge_cv_with_trans_target = TransformedTargetRegressor(
regressor=RidgeCV(),
transformer=QuantileTransformer(n_quantiles=900, output_distribution="normal"),
).fit(X_train, y_train)
y_pred_ridge_with_trans_target = ridge_cv_with_trans_target.predict(X_test)
# plot the actual vs predicted values
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge,
kind="actual_vs_predicted",
ax=ax0[0],
scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge_with_trans_target,
kind="actual_vs_predicted",
ax=ax0[1],
scatter_kwargs={"alpha": 0.5},
)
# Add the score in the legend of each axis
for ax, y_pred in zip([ax0[0], ax0[1]], [y_pred_ridge, y_pred_ridge_with_trans_target]):
for name, score in compute_score(y_test, y_pred).items():
ax.plot([], [], " ", label=f"{name}={score}")
ax.legend(loc="upper left")
ax0[0].set_title("Ridge regression \n without target transformation")
ax0[1].set_title("Ridge regression \n with target transformation")
# plot the residuals vs the predicted values
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge,
kind="residual_vs_predicted",
ax=ax1[0],
scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
y_test,
y_pred_ridge_with_trans_target,
kind="residual_vs_predicted",
ax=ax1[1],
scatter_kwargs={"alpha": 0.5},
)
ax1[0].set_title("Ridge regression \n without target transformation")
ax1[1].set_title("Ridge regression \n with target transformation")
f.suptitle("Ames housing data: selling price", y=1.05)
plt.tight_layout()
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 1,163 Sekunden)
Verwandte Beispiele
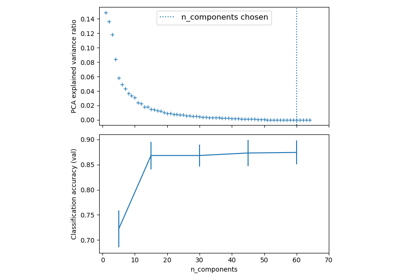
Pipelining: Verkettung einer PCA und einer logistischen Regression