Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Gradient Boosting Regularisierung#
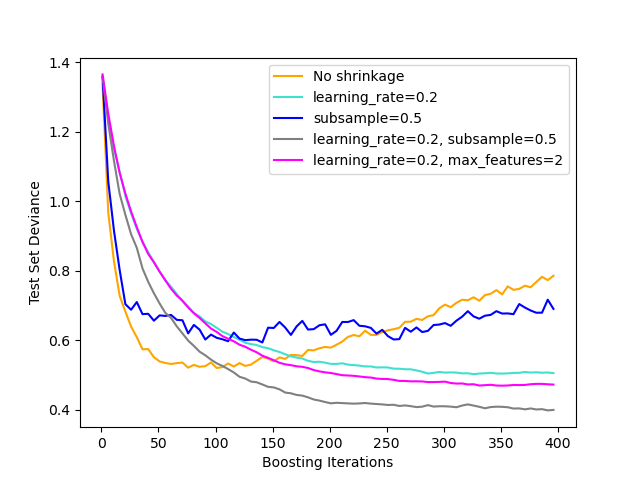
Illustration der Auswirkungen verschiedener Regularisierungsstrategien für Gradient Boosting. Das Beispiel stammt aus Hastie et al 2009 [1].
Die verwendete Verlustfunktion ist binomale Devianz. Regularisierung durch Schrumpfung (learning_rate < 1.0) verbessert die Leistung erheblich. In Kombination mit Schrumpfung kann stochastisches Gradient Boosting (subsample < 1.0) genauere Modelle durch Reduzierung der Varianz mittels Bagging erzeugen. Subsampling ohne Schrumpfung schneidet normalerweise schlecht ab. Eine weitere Strategie zur Reduzierung der Varianz ist das Subsampling der Merkmale analog zu den zufälligen Aufteilungen in Random Forests (über den Parameter max_features).
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
X, y = datasets.make_hastie_10_2(n_samples=4000, random_state=1)
# map labels from {-1, 1} to {0, 1}
labels, y = np.unique(y, return_inverse=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.8, random_state=0)
original_params = {
"n_estimators": 400,
"max_leaf_nodes": 4,
"max_depth": None,
"random_state": 2,
"min_samples_split": 5,
}
plt.figure()
for label, color, setting in [
("No shrinkage", "orange", {"learning_rate": 1.0, "subsample": 1.0}),
("learning_rate=0.2", "turquoise", {"learning_rate": 0.2, "subsample": 1.0}),
("subsample=0.5", "blue", {"learning_rate": 1.0, "subsample": 0.5}),
(
"learning_rate=0.2, subsample=0.5",
"gray",
{"learning_rate": 0.2, "subsample": 0.5},
),
(
"learning_rate=0.2, max_features=2",
"magenta",
{"learning_rate": 0.2, "max_features": 2},
),
]:
params = dict(original_params)
params.update(setting)
clf = ensemble.GradientBoostingClassifier(**params)
clf.fit(X_train, y_train)
# compute test set deviance
test_deviance = np.zeros((params["n_estimators"],), dtype=np.float64)
for i, y_proba in enumerate(clf.staged_predict_proba(X_test)):
test_deviance[i] = 2 * log_loss(y_test, y_proba[:, 1])
plt.plot(
(np.arange(test_deviance.shape[0]) + 1)[::5],
test_deviance[::5],
"-",
color=color,
label=label,
)
plt.legend(loc="upper right")
plt.xlabel("Boosting Iterations")
plt.ylabel("Test Set Deviance")
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 6,976 Sekunden)
Verwandte Beispiele
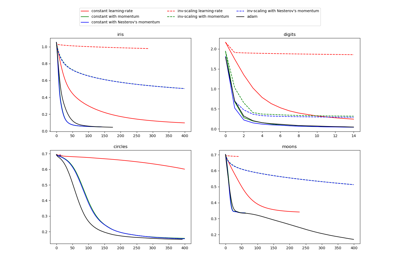
Vergleich von stochastischen Lernstrategien für MLPClassifier
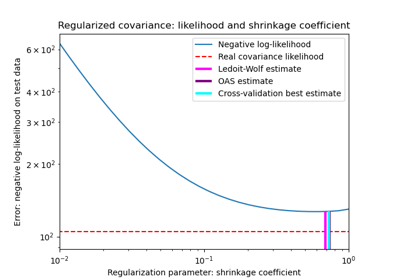
Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood