Hinweis

Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

Vergleich von Kernel Ridge Regression und SVR#

Sowohl Kernel Ridge Regression (KRR) als auch SVR lernen eine nichtlineare Funktion, indem sie den Kernel-Trick anwenden, d. h. sie lernen eine lineare Funktion im durch den jeweiligen Kernel induzierten Raum, was einer nichtlinearen Funktion im ursprünglichen Raum entspricht. Sie unterscheiden sich in den Verlustfunktionen (Ridge- versus Epsilon-insensitiven Verlust). Im Gegensatz zu SVR kann das Anpassen einer KRR geschlossener Form erfolgen und ist für mittelgroße Datensätze typischerweise schneller. Auf der anderen Seite ist das gelernte Modell nicht spärlich und somit zur Vorhersagezeit langsamer als SVR.

Dieses Beispiel illustriert beide Methoden anhand eines künstlichen Datensatzes, der eine sinusförmige Zielfunktion und starke Rauschen auf jedem fünften Datenpunkt enthält.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Beispieldaten generieren#

import numpy as np

rng = np.random.RandomState(42)

X = 5 * rng.rand(10000, 1)
y = np.sin(X).ravel()

# Add noise to targets
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))

X_plot = np.linspace(0, 5, 100000)[:, None]

Konstruktion der Kernel-basierten Regressionsmodelle#

from sklearn.kernel_ridge import KernelRidge
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR

train_size = 100

svr = GridSearchCV(
    SVR(kernel="rbf", gamma=0.1),
    param_grid={"C": [1e0, 1e1, 1e2, 1e3], "gamma": np.logspace(-2, 2, 5)},
)

kr = GridSearchCV(
    KernelRidge(kernel="rbf", gamma=0.1),
    param_grid={"alpha": [1e0, 0.1, 1e-2, 1e-3], "gamma": np.logspace(-2, 2, 5)},
)

Vergleich der Zeiten von SVR und Kernel Ridge Regression#

import time

t0 = time.time()
svr.fit(X[:train_size], y[:train_size])
svr_fit = time.time() - t0
print(f"Best SVR with params: {svr.best_params_} and R2 score: {svr.best_score_:.3f}")
print("SVR complexity and bandwidth selected and model fitted in %.3f s" % svr_fit)

t0 = time.time()
kr.fit(X[:train_size], y[:train_size])
kr_fit = time.time() - t0
print(f"Best KRR with params: {kr.best_params_} and R2 score: {kr.best_score_:.3f}")
print("KRR complexity and bandwidth selected and model fitted in %.3f s" % kr_fit)

sv_ratio = svr.best_estimator_.support_.shape[0] / train_size
print("Support vector ratio: %.3f" % sv_ratio)

t0 = time.time()
y_svr = svr.predict(X_plot)
svr_predict = time.time() - t0
print("SVR prediction for %d inputs in %.3f s" % (X_plot.shape[0], svr_predict))

t0 = time.time()
y_kr = kr.predict(X_plot)
kr_predict = time.time() - t0
print("KRR prediction for %d inputs in %.3f s" % (X_plot.shape[0], kr_predict))

Best SVR with params: {'C': 1.0, 'gamma': np.float64(0.1)} and R2 score: 0.737
SVR complexity and bandwidth selected and model fitted in 0.512 s
Best KRR with params: {'alpha': 0.1, 'gamma': np.float64(0.1)} and R2 score: 0.723
KRR complexity and bandwidth selected and model fitted in 0.190 s
Support vector ratio: 0.340
SVR prediction for 100000 inputs in 0.113 s
KRR prediction for 100000 inputs in 1.433 s

Betrachtung der Ergebnisse#

import matplotlib.pyplot as plt

sv_ind = svr.best_estimator_.support_
plt.scatter(
    X[sv_ind],
    y[sv_ind],
    c="r",
    s=50,
    label="SVR support vectors",
    zorder=2,
    edgecolors=(0, 0, 0),
)
plt.scatter(X[:100], y[:100], c="k", label="data", zorder=1, edgecolors=(0, 0, 0))
plt.plot(
    X_plot,
    y_svr,
    c="r",
    label="SVR (fit: %.3fs, predict: %.3fs)" % (svr_fit, svr_predict),
)
plt.plot(
    X_plot, y_kr, c="g", label="KRR (fit: %.3fs, predict: %.3fs)" % (kr_fit, kr_predict)
)
plt.xlabel("data")
plt.ylabel("target")
plt.title("SVR versus Kernel Ridge")
_ = plt.legend()

Die vorherige Abbildung vergleicht das gelernte Modell von KRR und SVR, wenn sowohl Komplexität/Regularisierung als auch Bandbreite des RBF-Kernels mittels Grid-Search optimiert werden. Die gelernten Funktionen sind sehr ähnlich; das Anpassen von KRR ist jedoch ungefähr 3-4 Mal schneller als das Anpassen von SVR (beide mit Grid-Search).

Die Vorhersage von 100.000 Zielwerten könnte theoretisch mit SVR etwa dreimal schneller sein, da es ein spärliches Modell mit nur etwa 1/3 der Trainingsdatenpunkte als Stützvektoren gelernt hat. In der Praxis ist dies jedoch nicht unbedingt der Fall, da Implementierungsdetails bei der Berechnung der Kernel-Funktion für jedes Modell dazu führen können, dass das KRR-Modell genauso schnell oder sogar schneller ist, obwohl mehr arithmetische Operationen durchgeführt werden.

Visualisierung von Trainings- und Vorhersagezeiten#

plt.figure()

sizes = np.logspace(1, 3.8, 7).astype(int)
for name, estimator in {
    "KRR": KernelRidge(kernel="rbf", alpha=0.01, gamma=10),
    "SVR": SVR(kernel="rbf", C=1e2, gamma=10),
}.items():
    train_time = []
    test_time = []
    for train_test_size in sizes:
        t0 = time.time()
        estimator.fit(X[:train_test_size], y[:train_test_size])
        train_time.append(time.time() - t0)

        t0 = time.time()
        estimator.predict(X_plot[:1000])
        test_time.append(time.time() - t0)

    plt.plot(
        sizes,
        train_time,
        "o-",
        color="r" if name == "SVR" else "g",
        label="%s (train)" % name,
    )
    plt.plot(
        sizes,
        test_time,
        "o--",
        color="r" if name == "SVR" else "g",
        label="%s (test)" % name,
    )

plt.xscale("log")
plt.yscale("log")
plt.xlabel("Train size")
plt.ylabel("Time (seconds)")
plt.title("Execution Time")
_ = plt.legend(loc="best")

Diese Abbildung vergleicht die Zeit für das Anpassen und die Vorhersage von KRR und SVR für verschiedene Größen des Trainingsdatensatzes. Das Anpassen von KRR ist für mittelgroße Trainingsdatensätze (weniger als einige tausend Stichproben) schneller als SVR; für größere Trainingsdatensätze skaliert SVR jedoch besser. In Bezug auf die Vorhersagezeit sollte SVR für alle Größen des Trainingsdatensatzes schneller sein als KRR, da es eine spärliche Lösung gelernt hat. In der Praxis ist dies jedoch aufgrund von Implementierungsdetails nicht unbedingt der Fall. Beachten Sie, dass der Grad der Sparsity und damit die Vorhersagezeit von den Parametern Epsilon und C des SVR abhängen.

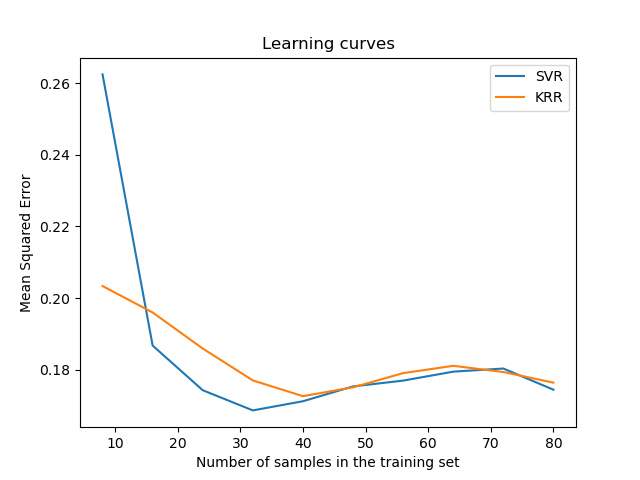
Visualisierung der Lernkurven#

from sklearn.model_selection import LearningCurveDisplay

_, ax = plt.subplots()

svr = SVR(kernel="rbf", C=1e1, gamma=0.1)
kr = KernelRidge(kernel="rbf", alpha=0.1, gamma=0.1)

common_params = {
    "X": X[:100],
    "y": y[:100],
    "train_sizes": np.linspace(0.1, 1, 10),
    "scoring": "neg_mean_squared_error",
    "negate_score": True,
    "score_name": "Mean Squared Error",
    "score_type": "test",
    "std_display_style": None,
    "ax": ax,
}

LearningCurveDisplay.from_estimator(svr, **common_params)
LearningCurveDisplay.from_estimator(kr, **common_params)
ax.set_title("Learning curves")
ax.legend(handles=ax.get_legend_handles_labels()[0], labels=["SVR", "KRR"])

plt.show()

Gesamtlaufzeit des Skripts: (0 Minuten 14,356 Sekunden)

Verwandte Beispiele

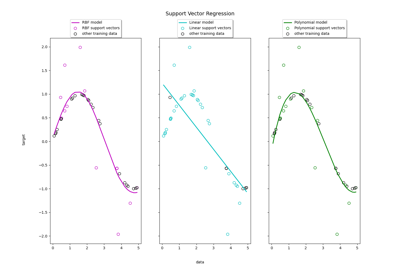
Support Vector Regression (SVR) mit linearen und nicht-linearen Kernen

RBF SVM Parameter

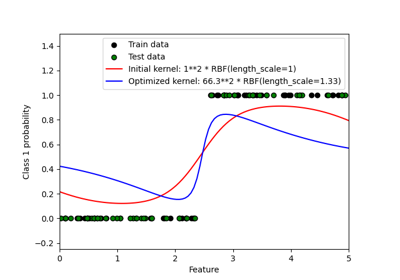
Probabilistische Vorhersagen mit Gauß-Prozess-Klassifikation (GPC)

Gesichtserkennungsbeispiel mit Eigenfaces und SVMs

Galerie generiert von Sphinx-Gallery