Hinweis
Zum Ende gehen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Permutations-Wichtigkeit im Vergleich zur Zufallswald-Feature-Wichtigkeit (MDI)#
In diesem Beispiel vergleichen wir die auf Verunreinigung basierende Feature-Wichtigkeit von RandomForestClassifier mit der Permutations-Wichtigkeit auf dem Titanic-Datensatz unter Verwendung von permutation_importance. Wir werden zeigen, dass die auf Verunreinigung basierende Feature-Wichtigkeit die Wichtigkeit numerischer Merkmale aufblähen kann.
Darüber hinaus leidet die auf Verunreinigung basierende Feature-Wichtigkeit von Zufallswäldern darunter, dass sie auf Statistiken berechnet wird, die aus dem Trainingsdatensatz abgeleitet sind: Die Wichtigkeiten können auch für Merkmale hoch sein, die das Zielvariable nicht vorhersagen, solange das Modell die Fähigkeit hat, sie zum Überanpassen zu nutzen.
Dieses Beispiel zeigt, wie Permutations-Wichtigkeiten als Alternative verwendet werden können, um diese Einschränkungen zu mildern.
Referenzen
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Daten laden und Feature Engineering#
Wir verwenden pandas, um eine Kopie des Titanic-Datensatzes zu laden. Das Folgende zeigt, wie separate Vorverarbeitung auf numerische und kategorische Merkmale angewendet wird.
Wir fügen zwei Zufallsvariablen hinzu, die keinerlei Korrelation mit der Zielvariable (survived) aufweisen.
random_numist eine numerische Variable mit hoher Kardinalität (so viele eindeutige Werte wie Datensätze).random_catist eine kategoriale Variable mit geringer Kardinalität (3 mögliche Werte).
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
X, y = fetch_openml("titanic", version=1, as_frame=True, return_X_y=True)
rng = np.random.RandomState(seed=42)
X["random_cat"] = rng.randint(3, size=X.shape[0])
X["random_num"] = rng.randn(X.shape[0])
categorical_columns = ["pclass", "sex", "embarked", "random_cat"]
numerical_columns = ["age", "sibsp", "parch", "fare", "random_num"]
X = X[categorical_columns + numerical_columns]
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
Wir definieren ein prädiktives Modell, das auf einem Zufallswald basiert. Daher werden wir die folgenden Vorverarbeitungsschritte durchführen:
Verwendung von
OrdinalEncoderzur Kodierung der kategorialen Merkmale;Verwendung von
SimpleImputerzum Auffüllen fehlender Werte für numerische Merkmale mit einer Mittelwertstrategie.
from sklearn.compose import ColumnTransformer
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OrdinalEncoder
categorical_encoder = OrdinalEncoder(
handle_unknown="use_encoded_value", unknown_value=-1, encoded_missing_value=-1
)
numerical_pipe = SimpleImputer(strategy="mean")
preprocessing = ColumnTransformer(
[
("cat", categorical_encoder, categorical_columns),
("num", numerical_pipe, numerical_columns),
],
verbose_feature_names_out=False,
)
rf = Pipeline(
[
("preprocess", preprocessing),
("classifier", RandomForestClassifier(random_state=42)),
]
)
rf.fit(X_train, y_train)
Genauigkeit des Modells#
Bevor die Feature-Wichtigkeiten inspiziert werden, ist es wichtig zu prüfen, ob die prädiktive Leistung des Modells ausreichend hoch ist. Tatsächlich wäre es von geringem Interesse, die wichtigen Merkmale eines nicht-prädiktiven Modells zu inspizieren.
print(f"RF train accuracy: {rf.score(X_train, y_train):.3f}")
print(f"RF test accuracy: {rf.score(X_test, y_test):.3f}")
RF train accuracy: 1.000
RF test accuracy: 0.814
Hier kann man beobachten, dass die Trainingsgenauigkeit sehr hoch ist (der Wald-Modell hat genügend Kapazität, um den Trainingssatz vollständig zu merken), aber er kann dank der integrierten Bagging-Methode von Zufallswäldern immer noch gut auf den Testdatensatz generalisieren.
Es ist möglicherweise möglich, einige Genauigkeit auf dem Trainingssatz gegen eine etwas bessere Genauigkeit auf dem Testdatensatz einzutauschen, indem die Kapazität der Bäume begrenzt wird (z. B. durch Setzen von min_samples_leaf=5 oder min_samples_leaf=10), um Überanpassung zu begrenzen, ohne zu viel Unteranpassung einzuführen.
Wir behalten jedoch vorerst unser Zufallswaldmodell mit hoher Kapazität bei, um einige Tücken bei der Feature-Wichtigkeit für Variablen mit vielen eindeutigen Werten zu veranschaulichen.
Baum-Feature-Wichtigkeit aus mittlerer Verringerung der Verunreinigung (MDI)#
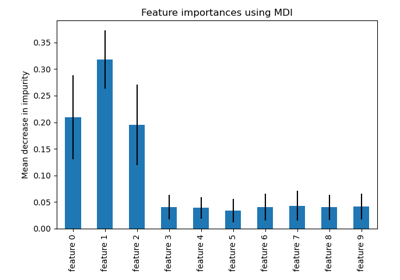
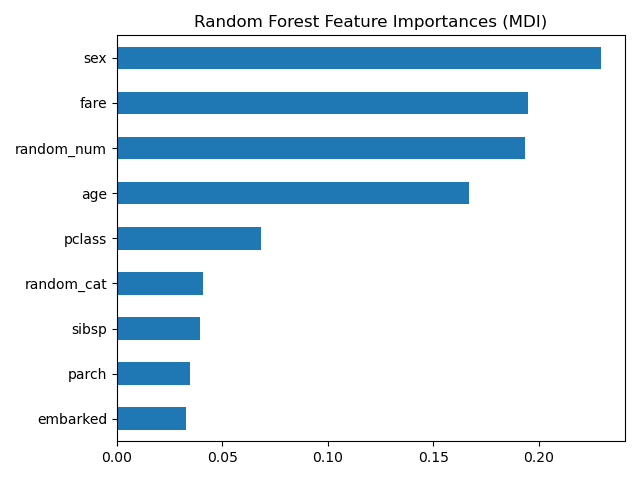
Die auf Verunreinigung basierende Feature-Wichtigkeit ordnet die numerischen Merkmale als die wichtigsten Merkmale ein. Infolgedessen wird die nicht-prädiktive Variable random_num als eines der wichtigsten Merkmale eingestuft!
Dieses Problem ergibt sich aus zwei Einschränkungen der auf Verunreinigung basierenden Feature-Wichtigkeiten:
auf Verunreinigung basierende Wichtigkeiten sind gegenüber Merkmalen mit hoher Kardinalität voreingenommen;
auf Verunreinigung basierende Wichtigkeiten werden auf Trainingssatz-Statistiken berechnet und spiegeln daher nicht die Fähigkeit eines Merkmals wider, nützlich für Vorhersagen zu sein, die auf den Testdatensatz generalisieren (wenn das Modell über genügend Kapazität verfügt).
Die Voreingenommenheit gegenüber Merkmalen mit hoher Kardinalität erklärt, warum random_num eine wirklich große Wichtigkeit im Vergleich zu random_cat hat, während wir erwarten würden, dass beide Zufallsmerkmale eine Null-Wichtigkeit haben.
Die Tatsache, dass wir Trainingssatz-Statistiken verwenden, erklärt, warum sowohl die Merkmale random_num als auch random_cat eine nicht-null Wichtigkeit aufweisen.
import pandas as pd
feature_names = rf[:-1].get_feature_names_out()
mdi_importances = pd.Series(
rf[-1].feature_importances_, index=feature_names
).sort_values(ascending=True)
ax = mdi_importances.plot.barh()
ax.set_title("Random Forest Feature Importances (MDI)")
ax.figure.tight_layout()
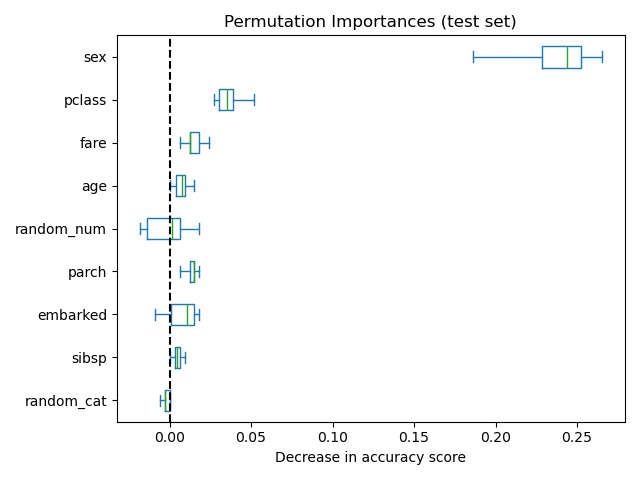
Als Alternative werden die Permutations-Wichtigkeiten von rf auf einem zurückgehaltenen Testdatensatz berechnet. Dies zeigt, dass das kategoriale Merkmal mit geringer Kardinalität, sex und pclass, die wichtigsten Merkmale sind. Tatsächlich führt das Vertauschen der Werte dieser Merkmale zu der größten Verringerung der Genauigkeitsbewertung des Modells auf dem Testdatensatz.
Beachten Sie auch, dass beide Zufallsmerkmale sehr geringe Wichtigkeiten (nahe 0) haben, wie erwartet.
from sklearn.inspection import permutation_importance
result = permutation_importance(
rf, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_importances_idx = result.importances_mean.argsort()
importances = pd.DataFrame(
result.importances[sorted_importances_idx].T,
columns=X.columns[sorted_importances_idx],
)
ax = importances.plot.box(vert=False, whis=10)
ax.set_title("Permutation Importances (test set)")
ax.axvline(x=0, color="k", linestyle="--")
ax.set_xlabel("Decrease in accuracy score")
ax.figure.tight_layout()

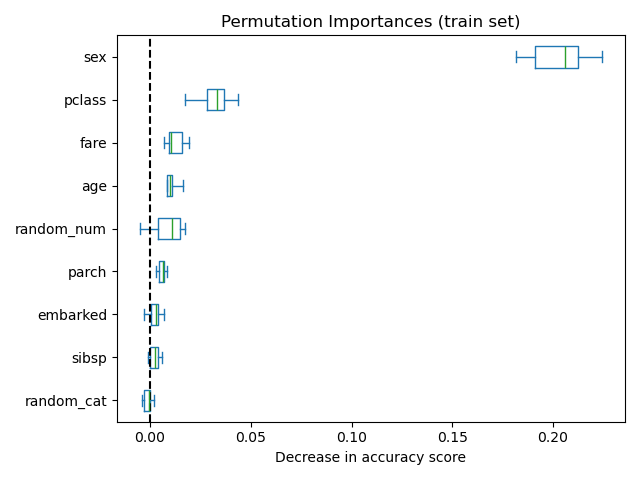
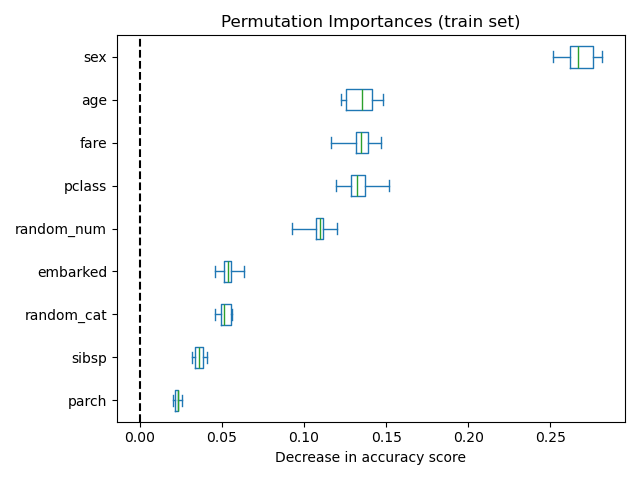
Es ist auch möglich, die Permutations-Wichtigkeiten auf dem Trainingsdatensatz zu berechnen. Dies zeigt, dass random_num und random_cat eine signifikant höhere Wichtigkeitsbewertung erhalten als wenn sie auf dem Testdatensatz berechnet werden. Der Unterschied zwischen diesen beiden Diagrammen ist eine Bestätigung dafür, dass das RF-Modell über genügend Kapazität verfügt, um diese zufälligen numerischen und kategorialen Merkmale zum Überanpassen zu nutzen.
result = permutation_importance(
rf, X_train, y_train, n_repeats=10, random_state=42, n_jobs=2
)
sorted_importances_idx = result.importances_mean.argsort()
importances = pd.DataFrame(
result.importances[sorted_importances_idx].T,
columns=X.columns[sorted_importances_idx],
)
ax = importances.plot.box(vert=False, whis=10)
ax.set_title("Permutation Importances (train set)")
ax.axvline(x=0, color="k", linestyle="--")
ax.set_xlabel("Decrease in accuracy score")
ax.figure.tight_layout()
Wir können das Experiment erneut versuchen, indem wir die Kapazität der Bäume zum Überanpassen begrenzen, indem wir min_samples_leaf auf 20 Datenpunkte setzen.
rf.set_params(classifier__min_samples_leaf=20).fit(X_train, y_train)
Wenn wir die Genauigkeitsbewertung auf dem Trainings- und Testdatensatz betrachten, stellen wir fest, dass die beiden Metriken jetzt sehr ähnlich sind. Daher überanpasst unser Modell nicht mehr. Wir können dann die Permutations-Wichtigkeiten mit diesem neuen Modell überprüfen.
print(f"RF train accuracy: {rf.score(X_train, y_train):.3f}")
print(f"RF test accuracy: {rf.score(X_test, y_test):.3f}")
RF train accuracy: 0.810
RF test accuracy: 0.832
train_result = permutation_importance(
rf, X_train, y_train, n_repeats=10, random_state=42, n_jobs=2
)
test_results = permutation_importance(
rf, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_importances_idx = train_result.importances_mean.argsort()
train_importances = pd.DataFrame(
train_result.importances[sorted_importances_idx].T,
columns=X.columns[sorted_importances_idx],
)
test_importances = pd.DataFrame(
test_results.importances[sorted_importances_idx].T,
columns=X.columns[sorted_importances_idx],
)
for name, importances in zip(["train", "test"], [train_importances, test_importances]):
ax = importances.plot.box(vert=False, whis=10)
ax.set_title(f"Permutation Importances ({name} set)")
ax.set_xlabel("Decrease in accuracy score")
ax.axvline(x=0, color="k", linestyle="--")
ax.figure.tight_layout()
Jetzt können wir beobachten, dass auf beiden Sätzen die Merkmale random_num und random_cat eine geringere Wichtigkeit haben als beim überanpassenden Zufallswald. Die Schlussfolgerungen bezüglich der Wichtigkeit der anderen Merkmale bleiben jedoch gültig.
Gesamtlaufzeit des Skripts: (0 Minuten 6,265 Sekunden)
Verwandte Beispiele
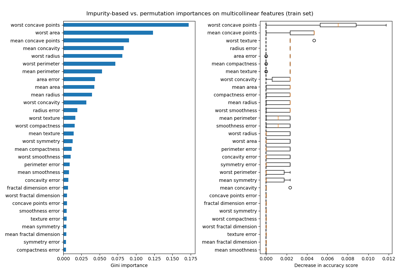
Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen