Nicht-negative kleinste Quadrate

In diesem Beispiel passen wir ein lineares Modell mit positiven Einschränkungen für die Regressionskoeffizienten an und vergleichen die geschätzten Koeffizienten mit einer klassischen linearen Regression.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.metrics import r2_score

Einige zufällige Daten generieren

np.random.seed(42)

n_samples, n_features = 200, 50
X = np.random.randn(n_samples, n_features)
true_coef = 3 * np.random.randn(n_features)
# Threshold coefficients to render them non-negative
true_coef[true_coef < 0] = 0
y = np.dot(X, true_coef)

# Add some noise
y += 5 * np.random.normal(size=(n_samples,))

Daten in Trainings- und Testdatensatz aufteilen

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)

Die Nicht-negativen kleinsten Quadrate anpassen.

from sklearn.linear_model import LinearRegression

reg_nnls = LinearRegression(positive=True)
y_pred_nnls = reg_nnls.fit(X_train, y_train).predict(X_test)
r2_score_nnls = r2_score(y_test, y_pred_nnls)
print("NNLS R2 score", r2_score_nnls)

NNLS R2 score 0.8225220806196525

Ein OLS anpassen.

reg_ols = LinearRegression()
y_pred_ols = reg_ols.fit(X_train, y_train).predict(X_test)
r2_score_ols = r2_score(y_test, y_pred_ols)
print("OLS R2 score", r2_score_ols)

OLS R2 score 0.7436926291700354

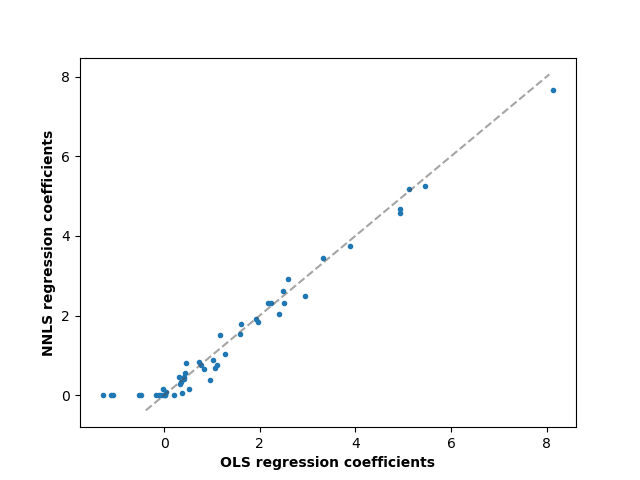
Beim Vergleich der Regressionskoeffizienten zwischen OLS und NNLS können wir beobachten, dass sie stark korreliert sind (die gestrichelte Linie ist die Identitätsrelation), aber die nicht-negative Einschränkung einige auf 0 schrumpft. Die nicht-negativen kleinsten Quadrate liefern inhärent spärliche Ergebnisse.

fig, ax = plt.subplots()
ax.plot(reg_ols.coef_, reg_nnls.coef_, linewidth=0, marker=".")

low_x, high_x = ax.get_xlim()
low_y, high_y = ax.get_ylim()
low = max(low_x, low_y)
high = min(high_x, high_y)
ax.plot([low, high], [low, high], ls="--", c=".3", alpha=0.5)
ax.set_xlabel("OLS regression coefficients", fontweight="bold")
ax.set_ylabel("NNLS regression coefficients", fontweight="bold")

Text(55.847222222222214, 0.5, 'NNLS regression coefficients')

Verwandte Beispiele

Gewöhnliche kleinste Quadrate und Ridge Regression

Gewöhnliche kleinste Quadrate und Ridge Regression

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Versagen des maschinellen Lernens bei der Inferenz kausaler Effekte

Versagen des maschinellen Lernens bei der Inferenz kausaler Effekte

L1-basierte Modelle für sparse Signale

L1-basierte Modelle für sparse Signale