Faktorenanalyse (mit Rotation) zur Visualisierung von Mustern

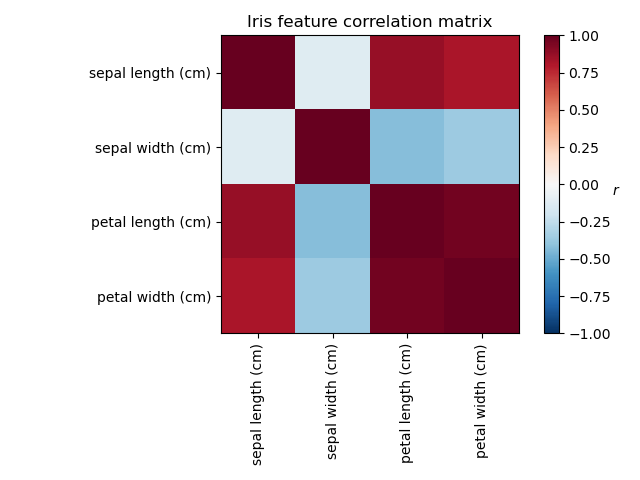
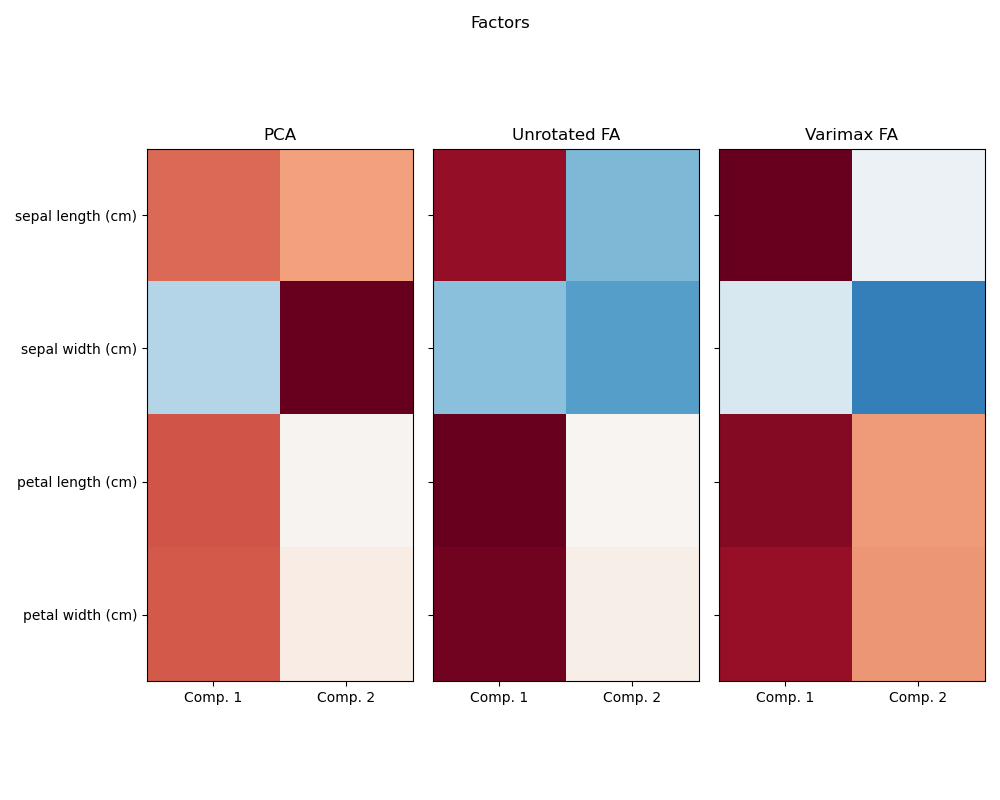
Bei der Untersuchung des Iris-Datensatzes stellen wir fest, dass Sepal Länge, Petal Länge und Petal Breite stark korreliert sind. Sepal Breite ist weniger redundant. Matrixdekompositionstechniken können diese latenten Muster aufdecken. Das Anwenden von Rotationen auf die resultierenden Komponenten verbessert den prädiktiven Wert des abgeleiteten latenten Raums nicht grundsätzlich, kann aber helfen, deren Struktur zu visualisieren. Hier findet beispielsweise die Varimax-Rotation, die durch Maximierung der quadrierten Varianzen der Gewichte ermittelt wird, eine Struktur, bei der die zweite Komponente nur positiv auf die Sepalbreite lädt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn.preprocessing import StandardScaler

Iris-Daten laden

data = load_iris()
X = StandardScaler().fit_transform(data["data"])
feature_names = data["feature_names"]

Kovarianz von Iris-Merkmalen plotten

ax = plt.axes()

im = ax.imshow(np.corrcoef(X.T), cmap="RdBu_r", vmin=-1, vmax=1)

ax.set_xticks([0, 1, 2, 3])
ax.set_xticklabels(list(feature_names), rotation=90)
ax.set_yticks([0, 1, 2, 3])
ax.set_yticklabels(list(feature_names))

plt.colorbar(im).ax.set_ylabel("$r$", rotation=0)
ax.set_title("Iris feature correlation matrix")
plt.tight_layout()

Faktorenanalyse mit Varimax-Rotation durchführen

n_comps = 2

methods = [
    ("PCA", PCA()),
    ("Unrotated FA", FactorAnalysis()),
    ("Varimax FA", FactorAnalysis(rotation="varimax")),
]
fig, axes = plt.subplots(ncols=len(methods), figsize=(10, 8), sharey=True)

for ax, (method, fa) in zip(axes, methods):
    fa.set_params(n_components=n_comps)
    fa.fit(X)

    components = fa.components_.T
    print("\n\n %s :\n" % method)
    print(components)

    vmax = np.abs(components).max()
    ax.imshow(components, cmap="RdBu_r", vmax=vmax, vmin=-vmax)
    ax.set_yticks(np.arange(len(feature_names)))
    ax.set_yticklabels(feature_names)
    ax.set_title(str(method))
    ax.set_xticks([0, 1])
    ax.set_xticklabels(["Comp. 1", "Comp. 2"])
fig.suptitle("Factors")
plt.tight_layout()
plt.show()

 PCA :

[[ 0.52106591  0.37741762]
 [-0.26934744  0.92329566]
 [ 0.5804131   0.02449161]
 [ 0.56485654  0.06694199]]


 Unrotated FA :

[[ 0.88096009 -0.4472869 ]
 [-0.41691605 -0.55390036]
 [ 0.99918858  0.01915283]
 [ 0.96228895  0.05840206]]


 Varimax FA :

[[ 0.98633022 -0.05752333]
 [-0.16052385 -0.67443065]
 [ 0.90809432  0.41726413]
 [ 0.85857475  0.43847489]]

Verwandte Beispiele

Principal Component Analysis (PCA) auf dem Iris-Datensatz

Principal Component Analysis (PCA) auf dem Iris-Datensatz

Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

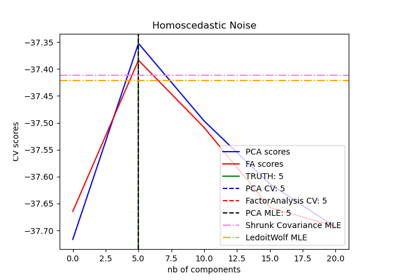
Modellauswahl mit Probabilistischem PCA und Faktorenanalyse (FA)

Modellauswahl mit Probabilistischem PCA und Faktorenanalyse (FA)

Zerlegung von Gesicht-Datensätzen

Zerlegung von Gesicht-Datensätzen