Hierarchisches Clustering mit und ohne Struktur

Dieses Beispiel demonstriert hierarchisches Clustering mit und ohne Konnektivitätsbeschränkungen. Es zeigt den Effekt der Einführung eines Konnektivitätsgraphen zur Erfassung lokaler Strukturen in den Daten. Ohne Konnektivitätsbeschränkungen basiert das Clustering rein auf der Distanz, während mit Beschränkungen das Clustering lokale Strukturen berücksichtigt.

Weitere Informationen finden Sie unter Hierarchisches Clustering.

Das Erzwingen von Konnektivität hat zwei Vorteile. Erstens ist das Clustering mit dünnen Konnektivitätsmatrizen im Allgemeinen schneller.

Zweitens sind bei Verwendung einer Konnektivitätsmatrix Single-, Average- und Complete-Linkage instabil und neigen dazu, wenige Cluster zu bilden, die sehr schnell wachsen. Tatsächlich kämpfen Average- und Complete-Linkage gegen dieses Perkolationsverhalten, indem sie alle Distanzen zwischen zwei Clustern berücksichtigen, wenn sie zusammengeführt werden (während Single-Linkage das Verhalten durch Berücksichtigung der kürzesten Distanz zwischen Clustern übertreibt). Der Konnektivitätsgraph bricht diesen Mechanismus für Average- und Complete-Linkage und lässt sie dem zerbrechlicheren Single-Linkage ähneln. Dieser Effekt ist bei sehr dünnen Graphen ausgeprägter (versuchen Sie, die Anzahl der Nachbarn in kneighbors_graph zu verringern) und bei Complete-Linkage. Insbesondere die geringe Anzahl von Nachbarn im Graphen erzwingt eine Geometrie, die der von Single-Linkage nahekommt, die bekanntermaßen diese Perkolationsinstabilität aufweist.

Der Effekt der Erzwingung von Konnektivität wird anhand von zwei unterschiedlichen, aber ähnlichen Datensätzen veranschaulicht, die eine spiralförmige Struktur zeigen. Im ersten Beispiel erstellen wir einen Swiss-Roll-Datensatz und führen hierarchisches Clustering auf der Position der Daten durch. Hier vergleichen wir unstrukturiertes Ward-Clustering mit einer strukturierten Variante, die k-Nearest-Neighbors-Konnektivität erzwingt. Im zweiten Beispiel schließen wir die Auswirkungen der Anwendung eines solchen Konnektivitätsgraphen auf Single-, Average- und Complete-Linkage ein.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Generieren des Swiss-Roll-Datensatzes.

import time

from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll

n_samples = 1500
noise = 0.05
X1, _ = make_swiss_roll(n_samples, noise=noise)
X1[:, 1] *= 0.5  # Make the roll thinner

Clustering ohne Konnektivitätsbeschränkungen berechnen

print("Compute unstructured hierarchical clustering...")
st = time.time()
ward_unstructured = AgglomerativeClustering(n_clusters=6, linkage="ward").fit(X1)
elapsed_time_unstructured = time.time() - st
label_unstructured = ward_unstructured.labels_
print(f"Elapsed time: {elapsed_time_unstructured:.2f}s")
print(f"Number of points: {label_unstructured.size}")

Compute unstructured hierarchical clustering...
Elapsed time: 0.03s
Number of points: 1500

Ergebnis des unstrukturierten Clusterings plotten

import matplotlib.pyplot as plt
import numpy as np

fig1 = plt.figure()
ax1 = fig1.add_subplot(111, projection="3d", elev=7, azim=-80)
ax1.set_position([0, 0, 0.95, 1])
for l in np.unique(label_unstructured):
    ax1.scatter(
        X1[label_unstructured == l, 0],
        X1[label_unstructured == l, 1],
        X1[label_unstructured == l, 2],
        color=plt.cm.jet(float(l) / np.max(label_unstructured + 1)),
        s=20,
        edgecolor="k",
    )
_ = fig1.suptitle(
    f"Without connectivity constraints (time {elapsed_time_unstructured:.2f}s)"
)

Clustering mit Konnektivitätsbeschränkungen berechnen

from sklearn.neighbors import kneighbors_graph

connectivity = kneighbors_graph(X1, n_neighbors=10, include_self=False)

print("Compute structured hierarchical clustering...")
st = time.time()
ward_structured = AgglomerativeClustering(
    n_clusters=6, connectivity=connectivity, linkage="ward"
).fit(X1)
elapsed_time_structured = time.time() - st
label_structured = ward_structured.labels_
print(f"Elapsed time: {elapsed_time_structured:.2f}s")
print(f"Number of points: {label_structured.size}")

Compute structured hierarchical clustering...
Elapsed time: 0.06s
Number of points: 1500

Ergebnis des strukturierten Clusterings plotten

fig2 = plt.figure()
ax2 = fig2.add_subplot(111, projection="3d", elev=7, azim=-80)
ax2.set_position([0, 0, 0.95, 1])
for l in np.unique(label_structured):
    ax2.scatter(
        X1[label_structured == l, 0],
        X1[label_structured == l, 1],
        X1[label_structured == l, 2],
        color=plt.cm.jet(float(l) / np.max(label_structured + 1)),
        s=20,
        edgecolor="k",
    )
_ = fig2.suptitle(
    f"With connectivity constraints (time {elapsed_time_structured:.2f}s)"
)

Generieren eines 2D-Spiral-Datensatzes.

n_samples = 1500
np.random.seed(0)
t = 1.5 * np.pi * (1 + 3 * np.random.rand(1, n_samples))
x = t * np.cos(t)
y = t * np.sin(t)

X2 = np.concatenate((x, y))
X2 += 0.7 * np.random.randn(2, n_samples)
X2 = X2.T

Lokale Konnektivität mithilfe eines Graphen erfassen

Eine größere Anzahl von Nachbarn ergibt homogenere Cluster auf Kosten der Rechenzeit. Eine sehr große Anzahl von Nachbarn ergibt gleichmäßig verteilte Clustergrößen, erzwingt aber möglicherweise nicht die lokale Mannigfaltigkeitsstruktur der Daten.

knn_graph = kneighbors_graph(X2, 30, include_self=False)

Clustering mit und ohne Struktur plotten

fig3 = plt.figure(figsize=(8, 12))
subfigs = fig3.subfigures(4, 1)
params = [
    (None, 30),
    (None, 3),
    (knn_graph, 30),
    (knn_graph, 3),
]

for subfig, (connectivity, n_clusters) in zip(subfigs, params):
    axs = subfig.subplots(1, 4, sharey=True)
    for index, linkage in enumerate(("average", "complete", "ward", "single")):
        model = AgglomerativeClustering(
            linkage=linkage, connectivity=connectivity, n_clusters=n_clusters
        )
        t0 = time.time()
        model.fit(X2)
        elapsed_time = time.time() - t0
        axs[index].scatter(
            X2[:, 0], X2[:, 1], c=model.labels_, cmap=plt.cm.nipy_spectral
        )
        axs[index].set_title(
            "linkage=%s\n(time %.2fs)" % (linkage, elapsed_time),
            fontdict=dict(verticalalignment="top"),
        )
        axs[index].set_aspect("equal")
        axs[index].axis("off")

        subfig.subplots_adjust(bottom=0, top=0.83, wspace=0, left=0, right=1)
        subfig.suptitle(
            "n_cluster=%i, connectivity=%r" % (n_clusters, connectivity is not None),
            size=17,
        )

plt.show()

Verwandte Beispiele

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

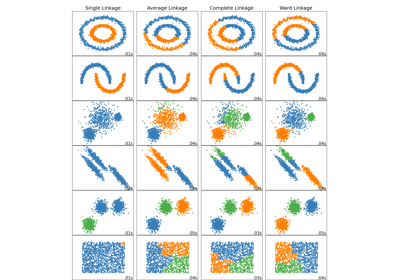
Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

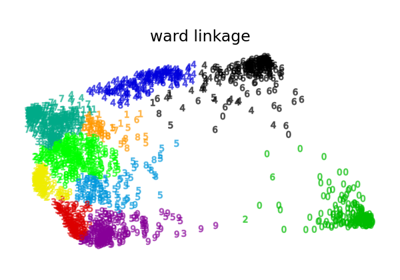
Verschiedenes Agglomeratives Clustering auf einer 2D-Einbettung von Ziffern

Verschiedenes Agglomeratives Clustering auf einer 2D-Einbettung von Ziffern

Vergleich verschiedener Clustering-Algorithmen auf Toy-Datensätzen

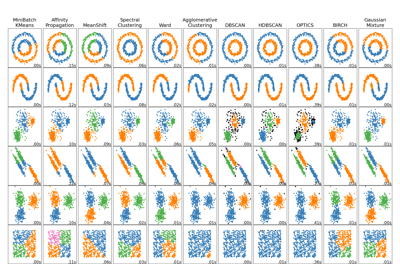
Vergleich verschiedener Clustering-Algorithmen auf Toy-Datensätzen