Quantilregression

Dieses Beispiel veranschaulicht, wie Quantilregression nicht-triviale bedingte Quantile vorhersagen kann.

Die linke Abbildung zeigt den Fall, in dem die Fehlerverteilung normal ist, aber eine nicht konstante Varianz aufweist, d. h. mit Heteroskedastizität.

Die rechte Abbildung zeigt ein Beispiel für eine asymmetrische Fehlerverteilung, nämlich die Pareto-Verteilung.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatzgenerierung

Um das Verhalten der Quantilregression zu veranschaulichen, werden wir zwei synthetische Datensätze generieren. Die wahren generativen Zufallsprozesse für beide Datensätze werden aus demselben Erwartungswert mit einer linearen Beziehung zu einem einzelnen Merkmal x bestehen.

import numpy as np

rng = np.random.RandomState(42)
x = np.linspace(start=0, stop=10, num=100)
X = x[:, np.newaxis]
y_true_mean = 10 + 0.5 * x

Wir werden zwei aufeinanderfolgende Probleme erstellen, indem wir die Verteilung des Zielwerts y ändern und denselben Erwartungswert beibehalten.

• Im ersten Fall wird ein heteroskedastisches normales Rauschen hinzugefügt;

• Im zweiten Fall wird ein asymmetrisches Pareto-Rauschen hinzugefügt.

y_normal = y_true_mean + rng.normal(loc=0, scale=0.5 + 0.5 * x, size=x.shape[0])
a = 5
y_pareto = y_true_mean + 10 * (rng.pareto(a, size=x.shape[0]) - 1 / (a - 1))

Lassen Sie uns zunächst die Datensätze sowie die Verteilung der Residuen y - mean(y) visualisieren.

import matplotlib.pyplot as plt

_, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 11), sharex="row", sharey="row")

axs[0, 0].plot(x, y_true_mean, label="True mean")
axs[0, 0].scatter(x, y_normal, color="black", alpha=0.5, label="Observations")
axs[1, 0].hist(y_true_mean - y_normal, edgecolor="black")


axs[0, 1].plot(x, y_true_mean, label="True mean")
axs[0, 1].scatter(x, y_pareto, color="black", alpha=0.5, label="Observations")
axs[1, 1].hist(y_true_mean - y_pareto, edgecolor="black")

axs[0, 0].set_title("Dataset with heteroscedastic Normal distributed targets")
axs[0, 1].set_title("Dataset with asymmetric Pareto distributed target")
axs[1, 0].set_title(
    "Residuals distribution for heteroscedastic Normal distributed targets"
)
axs[1, 1].set_title("Residuals distribution for asymmetric Pareto distributed target")
axs[0, 0].legend()
axs[0, 1].legend()
axs[0, 0].set_ylabel("y")
axs[1, 0].set_ylabel("Counts")
axs[0, 1].set_xlabel("x")
axs[0, 0].set_xlabel("x")
axs[1, 0].set_xlabel("Residuals")
_ = axs[1, 1].set_xlabel("Residuals")

Bei normalverteiltem Zielwert mit Heteroskedastizität beobachten wir, dass die Varianz des Rauschens zunimmt, wenn der Wert des Merkmals x zunimmt.

Bei einem asymmetrisch Pareto-verteilten Zielwert beobachten wir, dass die positiven Residuen begrenzt sind.

Diese Arten von verrauschten Zielen machen die Schätzung mittels LinearRegression weniger effizient, d. h. wir benötigen mehr Daten, um stabile Ergebnisse zu erzielen, und zusätzlich können große Ausreißer einen enormen Einfluss auf die angepassten Koeffizienten haben. (Anders ausgedrückt: In einer Umgebung mit konstanter Varianz konvergieren Ordinary Least Squares (OLS)-Schätzer mit zunehmender Stichprobengröße viel schneller zu den *wahren* Koeffizienten.)

In diesem asymmetrischen Setting geben der Median oder verschiedene Quantile zusätzliche Einblicke. Darüber hinaus ist die Medianschätzung viel robuster gegenüber Ausreißern und Verteilungen mit schweren Rändern. Beachten Sie jedoch, dass extreme Quantile durch sehr wenige Datenpunkte geschätzt werden. 95%-Quantile werden mehr oder weniger durch die 5% größten Werte geschätzt und sind daher auch etwas empfindlich gegenüber Ausreißern.

Im Rest dieses Tutorials zeigen wir, wie QuantileRegressor in der Praxis verwendet werden kann und geben Intuition für die Eigenschaften der angepassten Modelle. Schließlich vergleichen wir sowohl QuantileRegressor als auch LinearRegression.

Anpassen eines QuantileRegressor

In diesem Abschnitt möchten wir den bedingten Median sowie ein niedriges und ein hohes Quantil bei 5% bzw. 95% schätzen. Somit erhalten wir drei lineare Modelle, eines für jedes Quantil.

Wir verwenden die Quantile bei 5% und 95%, um die Ausreißer in der Trainingsstichprobe außerhalb des zentralen 90%-Intervalls zu finden.

from sklearn.linear_model import QuantileRegressor

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_normal).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_normal
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_normal
        )

Nun können wir die drei linearen Modelle und die unterschiedenen Stichproben plotten, die sich innerhalb des zentralen 90%-Intervalls befinden, von den Stichproben, die sich außerhalb dieses Intervalls befinden.

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_normal[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_normal[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of heteroscedastic Normal distributed target")

Da das Rauschen immer noch normalverteilt und insbesondere symmetrisch ist, stimmen der wahre bedingte Mittelwert und der wahre bedingte Median überein. Tatsächlich sehen wir, dass der geschätzte Median fast den wahren Mittelwert trifft. Wir beobachten den Effekt einer zunehmenden Rauschvarianz auf die 5% und 95% Quantile: Die Steigungen dieser Quantile sind sehr unterschiedlich und der Abstand zwischen ihnen wird mit zunehmendem x breiter.

Um zusätzliche Intuition für die Bedeutung der Schätzer für das 5% und 95% Quantil zu erhalten, kann man die Anzahl der Stichproben oberhalb und unterhalb der vorhergesagten Quantile (dargestellt durch ein Kreuz im obigen Diagramm) zählen, unter Berücksichtigung, dass wir insgesamt 100 Stichproben haben.

Wir können dasselbe Experiment mit dem asymmetrischen Pareto-verteilten Zielwert wiederholen.

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_pareto).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_pareto
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_pareto
        )

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_pareto[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_pareto[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of asymmetric Pareto distributed target")

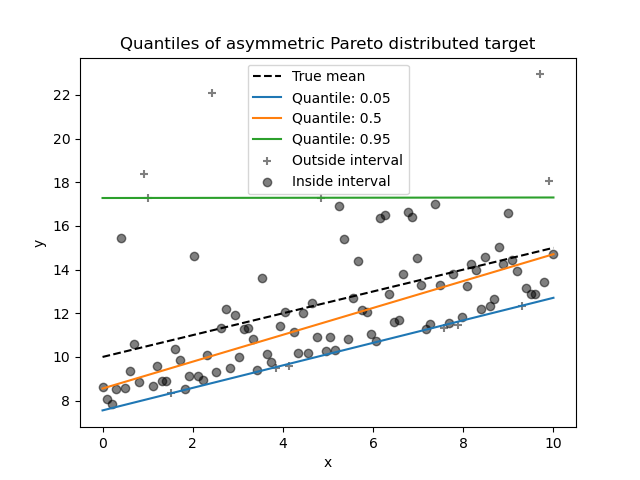
Aufgrund der Asymmetrie der Rauschverteilung beobachten wir, dass der wahre Mittelwert und der geschätzte bedingte Median unterschiedlich sind. Wir beobachten auch, dass jedes Quantilmodell unterschiedliche Parameter hat, um das gewünschte Quantil besser anzupassen. Beachten Sie, dass idealerweise alle Quantile in diesem Fall parallel wären, was mit mehr Datenpunkten oder weniger extremen Quantilen, z. B. 10% und 90%, deutlicher würde.

Vergleich von QuantileRegressor und LinearRegression

In diesem Abschnitt werden wir uns mit dem Unterschied der Verlustfunktionen befassen, die QuantileRegressor und LinearRegression minimieren.

Tatsächlich ist LinearRegression ein Ansatz der kleinsten Quadrate, der den mittleren quadratischen Fehler (MSE) zwischen den Trainings- und vorhergesagten Zielwerten minimiert. Im Gegensatz dazu minimiert QuantileRegressor mit quantile=0.5 stattdessen den mittleren absoluten Fehler (MAE).

Warum ist das wichtig? Die Verlustfunktionen geben an, was genau das Modell vorherzusagen versucht, siehe Benutzerhandbuch zur Auswahl der Scoring-Funktion. Kurz gesagt, ein Modell, das MSE minimiert, sagt den Mittelwert (Erwartungswert) voraus, und ein Modell, das MAE minimiert, sagt den Median voraus.

Lassen Sie uns die Trainingsfehler solcher Modelle in Bezug auf mittleren quadratischen Fehler und mittleren absoluten Fehler berechnen. Wir verwenden das asymmetrische Pareto-verteilte Ziel, um es interessanter zu machen, da Mittelwert und Median nicht gleich sind.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

linear_regression = LinearRegression()
quantile_regression = QuantileRegressor(quantile=0.5, alpha=0)

y_pred_lr = linear_regression.fit(X, y_pareto).predict(X)
y_pred_qr = quantile_regression.fit(X, y_pareto).predict(X)

print(
    "Training error (in-sample performance)\n"
    f"{'model':<20}   MAE   MSE\n"
    f"{linear_regression.__class__.__name__:<20} "
    f"{mean_absolute_error(y_pareto, y_pred_lr):5.3f} "
    f"{mean_squared_error(y_pareto, y_pred_lr):5.3f}\n"
    f"{quantile_regression.__class__.__name__:<20} "
    f"{mean_absolute_error(y_pareto, y_pred_qr):5.3f} "
    f"{mean_squared_error(y_pareto, y_pred_qr):5.3f}"
)

Training error (in-sample performance)
model                  MAE   MSE
LinearRegression     1.805 6.486
QuantileRegressor    1.670 7.025

Auf dem Trainingsdatensatz sehen wir, dass MAE für QuantileRegressor niedriger ist als für LinearRegression. Im Gegensatz dazu ist MSE für LinearRegression niedriger als für QuantileRegressor. Diese Ergebnisse bestätigen, dass MAE der von QuantileRegressor minimierte Verlust ist, während MSE der von LinearRegression minimierte Verlust ist.

Wir können eine ähnliche Bewertung vornehmen, indem wir den Testfehler betrachten, der durch Kreuzvalidierung erhalten wird.

from sklearn.model_selection import cross_validate

cv_results_lr = cross_validate(
    linear_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
cv_results_qr = cross_validate(
    quantile_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
print(
    "Test error (cross-validated performance)\n"
    f"{'model':<20}   MAE   MSE\n"
    f"{linear_regression.__class__.__name__:<20} "
    f"{-cv_results_lr['test_neg_mean_absolute_error'].mean():5.3f} "
    f"{-cv_results_lr['test_neg_mean_squared_error'].mean():5.3f}\n"
    f"{quantile_regression.__class__.__name__:<20} "
    f"{-cv_results_qr['test_neg_mean_absolute_error'].mean():5.3f} "
    f"{-cv_results_qr['test_neg_mean_squared_error'].mean():5.3f}"
)

Test error (cross-validated performance)
model                  MAE   MSE
LinearRegression     1.732 6.690
QuantileRegressor    1.679 7.129

Wir kommen zu ähnlichen Schlussfolgerungen bei der Auswertung außerhalb der Stichprobe.

Verwandte Beispiele

Vorhersageintervalle für Gradient Boosting Regression

Vorhersageintervalle für Gradient Boosting Regression

Release Highlights für scikit-learn 1.1

Release Highlights für scikit-learn 1.1

Verzögerte Merkmale für Zeitreihen-Prognose

Verzögerte Merkmale für Zeitreihen-Prognose

Demonstration von K-Means Annahmen

Demonstration von K-Means Annahmen