Robuste lineare Schätzeranpassung

Hier wird eine Sinusfunktion mit einem Polynom 3. Grades für Werte nahe Null angepasst.

Robuste Anpassung wird in verschiedenen Situationen demonstriert

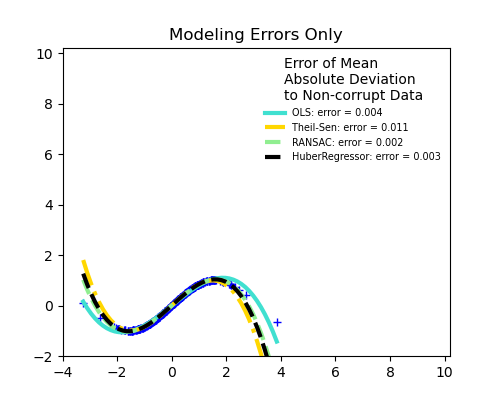
• Keine Messfehler, nur Modellierungsfehler (Anpassung einer Sinusfunktion mit einem Polynom)

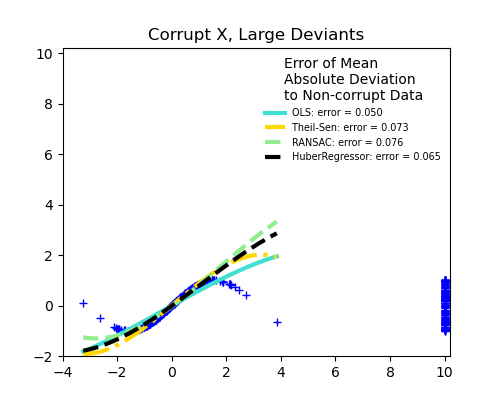
• Messfehler in X

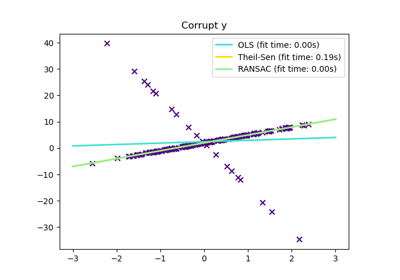
• Messfehler in y

Die mediane absolute Abweichung zu nicht verfälschten neuen Daten wird zur Beurteilung der Vorhersagequalität verwendet.

Was wir sehen können:

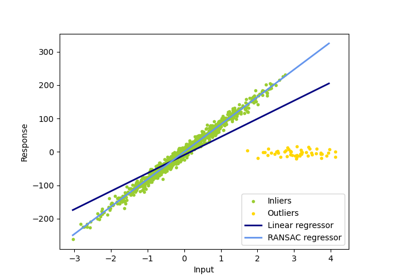
• RANSAC ist gut für starke Ausreißer in y-Richtung

• TheilSen ist gut für kleine Ausreißer, sowohl in X- als auch in y-Richtung, hat aber einen Schwellenwert, oberhalb dessen es schlechter als OLS abschneidet.

• Die Scores von HuberRegressor können nicht direkt mit TheilSen und RANSAC verglichen werden, da er nicht versucht, die Ausreißer vollständig zu filtern, sondern deren Einfluss zu verringern.

• 
• 
• 
• 
• 

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import numpy as np
from matplotlib import pyplot as plt

from sklearn.linear_model import (
    HuberRegressor,
    LinearRegression,
    RANSACRegressor,
    TheilSenRegressor,
)
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures

np.random.seed(42)

X = np.random.normal(size=400)
y = np.sin(X)
# Make sure that it X is 2D
X = X[:, np.newaxis]

X_test = np.random.normal(size=200)
y_test = np.sin(X_test)
X_test = X_test[:, np.newaxis]

y_errors = y.copy()
y_errors[::3] = 3

X_errors = X.copy()
X_errors[::3] = 3

y_errors_large = y.copy()
y_errors_large[::3] = 10

X_errors_large = X.copy()
X_errors_large[::3] = 10

estimators = [
    ("OLS", LinearRegression()),
    ("Theil-Sen", TheilSenRegressor(random_state=42)),
    ("RANSAC", RANSACRegressor(random_state=42)),
    ("HuberRegressor", HuberRegressor()),
]
colors = {
    "OLS": "turquoise",
    "Theil-Sen": "gold",
    "RANSAC": "lightgreen",
    "HuberRegressor": "black",
}
linestyle = {"OLS": "-", "Theil-Sen": "-.", "RANSAC": "--", "HuberRegressor": "--"}
lw = 3

x_plot = np.linspace(X.min(), X.max())
for title, this_X, this_y in [
    ("Modeling Errors Only", X, y),
    ("Corrupt X, Small Deviants", X_errors, y),
    ("Corrupt y, Small Deviants", X, y_errors),
    ("Corrupt X, Large Deviants", X_errors_large, y),
    ("Corrupt y, Large Deviants", X, y_errors_large),
]:
    plt.figure(figsize=(5, 4))
    plt.plot(this_X[:, 0], this_y, "b+")

    for name, estimator in estimators:
        model = make_pipeline(PolynomialFeatures(3), estimator)
        model.fit(this_X, this_y)
        mse = mean_squared_error(model.predict(X_test), y_test)
        y_plot = model.predict(x_plot[:, np.newaxis])
        plt.plot(
            x_plot,
            y_plot,
            color=colors[name],
            linestyle=linestyle[name],
            linewidth=lw,
            label="%s: error = %.3f" % (name, mse),
        )

    legend_title = "Error of Mean\nAbsolute Deviation\nto Non-corrupt Data"
    legend = plt.legend(
        loc="upper right", frameon=False, title=legend_title, prop=dict(size="x-small")
    )
    plt.xlim(-4, 10.2)
    plt.ylim(-2, 10.2)
    plt.title(title)
plt.show()

Verwandte Beispiele

Theil-Sen Regression

Theil-Sen Regression

Robuste lineare Modellschätzung mit RANSAC

Robuste lineare Modellschätzung mit RANSAC

Vergleich von linearen Bayes'schen Regressoren

Vergleich von linearen Bayes'schen Regressoren

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

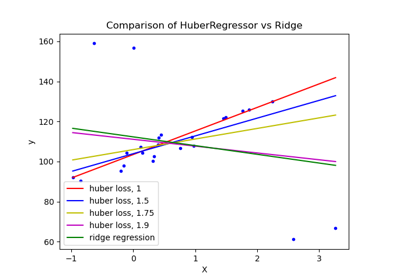
HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern