FastICA auf 2D-Punktwolken

Dieses Beispiel veranschaulicht visuell im Merkmalsraum einen Vergleich der Ergebnisse zweier verschiedener Komponententechniken.

Independent Component Analysis (ICA) vs Principal Component Analysis (PCA).

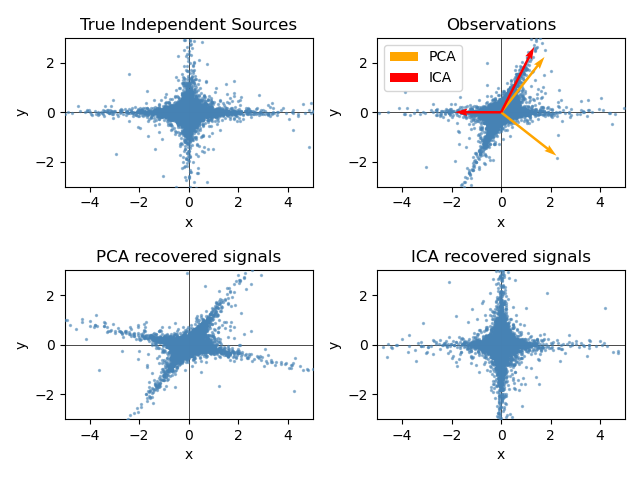
Die Darstellung von ICA im Merkmalsraum vermittelt die Sichtweise von „geometrischer ICA“: ICA ist ein Algorithmus, der Richtungen im Merkmalsraum findet, die Projektionen mit hoher Nicht-Gaußsität entsprechen. Diese Richtungen müssen im ursprünglichen Merkmalsraum nicht orthogonal sein, aber sie sind im geweißten Merkmalsraum orthogonal, in dem alle Richtungen der gleichen Varianz entsprechen.

PCA hingegen findet orthogonale Richtungen im Rohmerkmalsraum, die Richtungen entsprechen, die die maximale Varianz erklären.

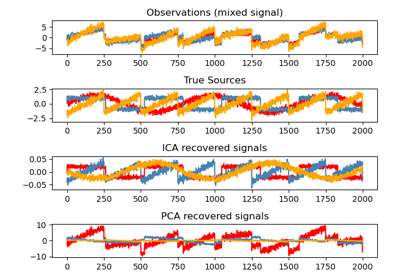
Hier simulieren wir unabhängige Quellen mithilfe eines stark nicht-gaußschen Prozesses, einer Student-T-Verteilung mit wenigen Freiheitsgraden (obere linke Abbildung). Wir mischen sie, um Beobachtungen zu erzeugen (obere rechte Abbildung). Im Rohbeobachtungsraum werden die von PCA identifizierten Richtungen durch orangefarbene Vektoren dargestellt. Wir stellen das Signal im PCA-Raum dar, nach dem Weißen um die Varianz, die den PCA-Vektoren entspricht (unten links). Das Ausführen von ICA entspricht dem Finden einer Drehung in diesem Raum, um die Richtungen größter Nicht-Gaußsität zu identifizieren (unten rechts).

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Beispieldaten generieren

import numpy as np

from sklearn.decomposition import PCA, FastICA

rng = np.random.RandomState(42)
S = rng.standard_t(1.5, size=(20000, 2))
S[:, 0] *= 2.0

# Mix data
A = np.array([[1, 1], [0, 2]])  # Mixing matrix

X = np.dot(S, A.T)  # Generate observations

pca = PCA()
S_pca_ = pca.fit(X).transform(X)

ica = FastICA(random_state=rng, whiten="arbitrary-variance")
S_ica_ = ica.fit(X).transform(X)  # Estimate the sources

Ergebnisse plotten

import matplotlib.pyplot as plt


def plot_samples(S, axis_list=None):
    plt.scatter(
        S[:, 0], S[:, 1], s=2, marker="o", zorder=10, color="steelblue", alpha=0.5
    )
    if axis_list is not None:
        for axis, color, label in axis_list:
            x_axis, y_axis = axis / axis.std()
            plt.quiver(
                (0, 0),
                (0, 0),
                x_axis,
                y_axis,
                zorder=11,
                width=0.01,
                scale=6,
                color=color,
                label=label,
            )

    plt.hlines(0, -5, 5, color="black", linewidth=0.5)
    plt.vlines(0, -3, 3, color="black", linewidth=0.5)
    plt.xlim(-5, 5)
    plt.ylim(-3, 3)
    plt.gca().set_aspect("equal")
    plt.xlabel("x")
    plt.ylabel("y")


plt.figure()
plt.subplot(2, 2, 1)
plot_samples(S / S.std())
plt.title("True Independent Sources")

axis_list = [(pca.components_.T, "orange", "PCA"), (ica.mixing_, "red", "ICA")]
plt.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
legend = plt.legend(loc="upper left")
legend.set_zorder(100)

plt.title("Observations")

plt.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_))
plt.title("PCA recovered signals")

plt.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
plt.title("ICA recovered signals")

plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.36)
plt.tight_layout()
plt.show()

Verwandte Beispiele

Blind Source Separation mit FastICA

Blind Source Separation mit FastICA

Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

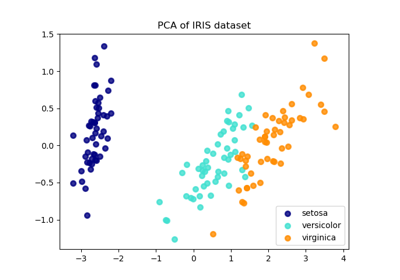
Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

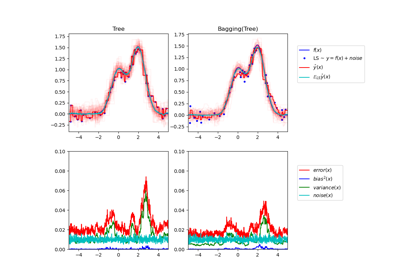
Einzelner Estimator versus Bagging: Bias-Varianz-Zerlegung

Einzelner Estimator versus Bagging: Bias-Varianz-Zerlegung

Principal Component Regression vs. Partial Least Squares Regression

Principal Component Regression vs. Partial Least Squares Regression