2.5. Dekomposition von Signalen in Komponenten (Matrixfaktorisierungsprobleme)

2.5.1. Hauptkomponentenanalyse (PCA)

2.5.1.1. Exakte PCA und probabilistische Interpretation

PCA wird verwendet, um einen multivariaten Datensatz in eine Menge aufeinanderfolgender orthogonaler Komponenten zu zerlegen, die eine maximale Varianz erklären. In scikit-learn wird PCA als Transformer-Objekt implementiert, das in seiner fit-Methode \(n\) Komponenten lernt und auf neuen Daten verwendet werden kann, um diese auf diese Komponenten zu projizieren.

PCA zentriert die Eingabedaten für jedes Merkmal, skaliert sie aber nicht, bevor die SVD angewendet wird. Der optionale Parameter whiten=True ermöglicht die Projektion der Daten in den singulären Raum, während jede Komponente auf die Einheitsvarianz skaliert wird. Dies ist oft nützlich, wenn nachgeschaltete Modelle starke Annahmen über die Isotropie des Signals treffen: Dies ist beispielsweise bei Support Vector Machines mit dem RBF-Kernel und dem K-Means-Clustering-Algorithmus der Fall.

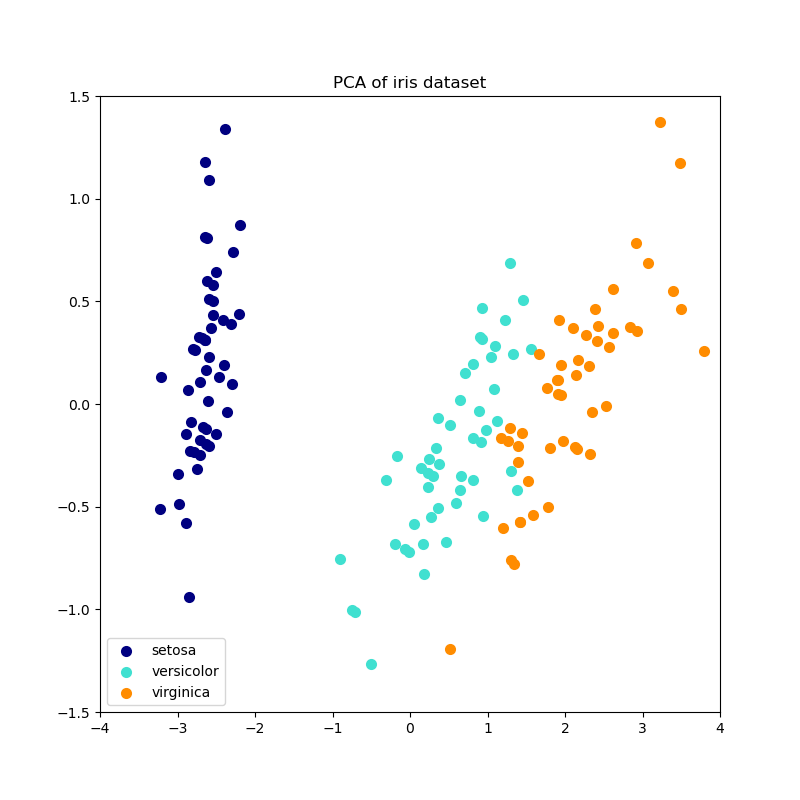
Im Folgenden finden Sie ein Beispiel für den Iris-Datensatz, der aus 4 Merkmalen besteht und auf die 2 Dimensionen projiziert wird, die die meiste Varianz erklären.

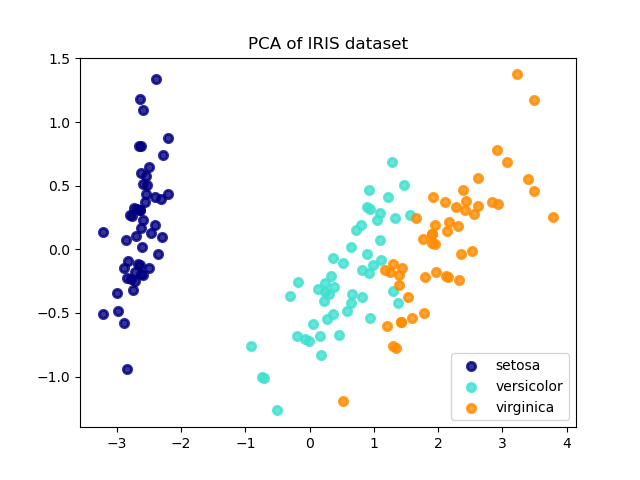
Das Objekt PCA bietet auch eine probabilistische Interpretation der PCA, die eine Wahrscheinlichkeit für Daten basierend auf der erklärten Varianz liefern kann. Daher implementiert es eine score-Methode, die in der Kreuzvalidierung verwendet werden kann.

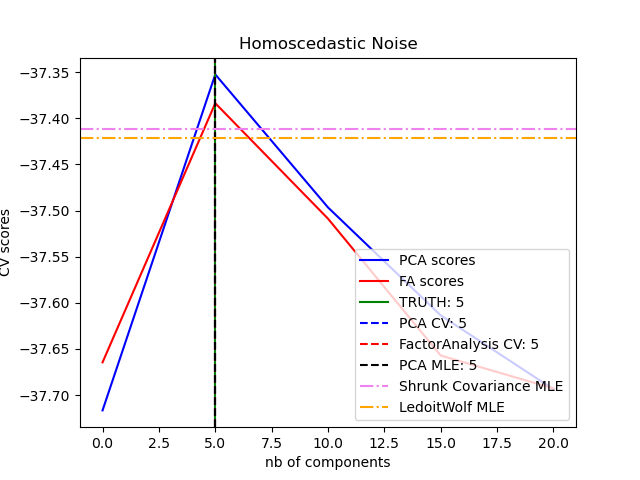
Beispiele

• Principal Component Analysis (PCA) auf dem Iris-Datensatz

• Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

• Modellauswahl mit Probabilistischem PCA und Faktorenanalyse (FA)

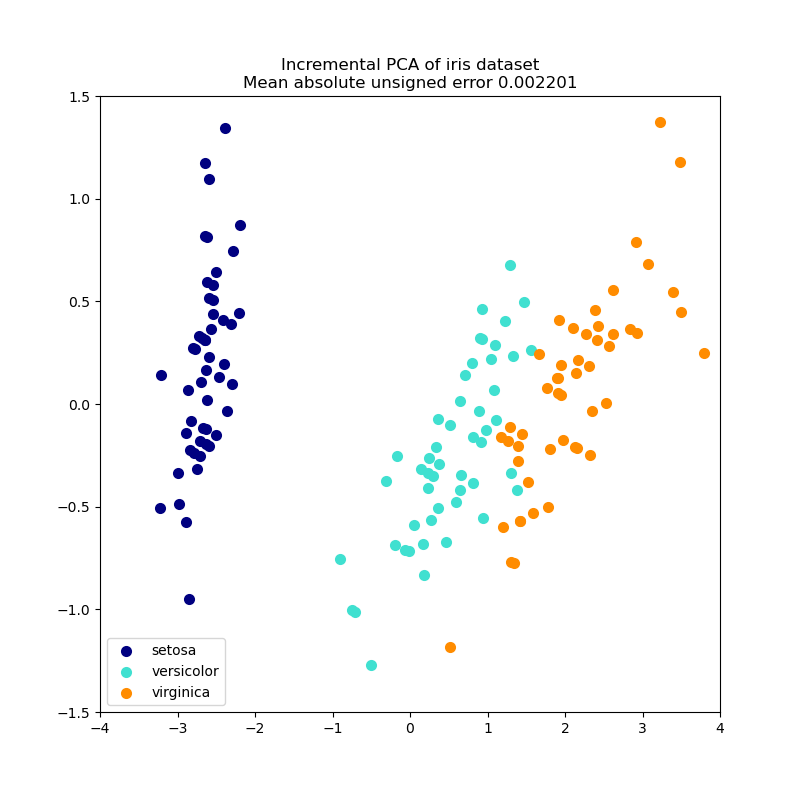
2.5.1.2. Inkrementelle PCA

Das Objekt PCA ist sehr nützlich, hat aber Einschränkungen für große Datensätze. Die größte Einschränkung besteht darin, dass PCA nur Batch-Verarbeitung unterstützt, was bedeutet, dass alle zu verarbeitenden Daten in den Hauptspeicher passen müssen. Das Objekt IncrementalPCA verwendet eine andere Verarbeitungsform und ermöglicht Teilberechnungen, die fast genau den Ergebnissen von PCA entsprechen, während die Daten in Minibatches verarbeitet werden. IncrementalPCA ermöglicht die Implementierung von Out-of-Core-Hauptkomponentenanalyse entweder durch

• Verwendung seiner partial_fit-Methode für Datenchucks, die sequenziell von der lokalen Festplatte oder einer Netzwerkdatenbank abgerufen werden.

• Aufruf seiner fit-Methode für eine speichergeordnete Datei mit numpy.memmap.

IncrementalPCA speichert nur Schätzungen der Komponenten- und Rauschvarianzen, um explained_variance_ratio_ inkrementell zu aktualisieren. Aus diesem Grund hängt die Speichernutzung von der Anzahl der Samples pro Batch ab, nicht von der Anzahl der zu verarbeitenden Samples im Datensatz.

Wie bei PCA zentriert IncrementalPCA die Eingabedaten für jedes Merkmal, skaliert sie aber nicht, bevor die SVD angewendet wird.

Beispiele

• Inkrementelles PCA

2.5.1.3. PCA mit randomisierter SVD

Es ist oft interessant, Daten in einen niedrigdimensionalen Raum zu projizieren, der den größten Teil der Varianz beibehält, indem die singulären Vektoren der Komponenten verworfen werden, die mit niedrigeren singulären Werten assoziiert sind.

Wenn wir beispielsweise mit 64x64 Pixel großen Graustufenbildern für die Gesichtserkennung arbeiten, beträgt die Dimensionalität der Daten 4096 und es ist langsam, einen RBF-Support-Vektor-Machine auf solchen breiten Daten zu trainieren. Außerdem wissen wir, dass die intrinsische Dimensionalität der Daten viel geringer als 4096 ist, da alle menschlichen Gesichter einigermaßen ähnlich aussehen. Die Stichproben liegen auf einer Mannigfaltigkeit viel geringerer Dimension (sagen wir zum Beispiel etwa 200). Der PCA-Algorithmus kann verwendet werden, um die Daten linear zu transformieren, während sowohl die Dimensionalität reduziert als auch die meiste erklärte Varianz gleichzeitig beibehalten wird.

Die Klasse PCA, die mit dem optionalen Parameter svd_solver='randomized' verwendet wird, ist in diesem Fall sehr nützlich: Da wir die meisten singulären Vektoren verwerfen werden, ist es viel effizienter, die Berechnung auf eine ungefähre Schätzung der zu behaltenden singulären Vektoren zu beschränken, um die Transformation tatsächlich durchzuführen.

Zum Beispiel zeigt die folgende Abbildung 16 Beispielporträts (zentriert um 0,0) aus dem Olivetti-Datensatz. Auf der rechten Seite sind die ersten 16 singulären Vektoren, die als Porträts umgeformt sind. Da wir nur die Top-16-Singulärvektoren eines Datensatzes der Größe \(n_{samples} = 400\) und \(n_{features} = 64 \times 64 = 4096\) benötigen, beträgt die Berechnungszeit weniger als 1 Sekunde.

Wenn wir \(n_{\max} = \max(n_{\mathrm{samples}}, n_{\mathrm{features}})\) und \(n_{\min} = \min(n_{\mathrm{samples}}, n_{\mathrm{features}})\) bezeichnen, beträgt die Zeitkomplexität der randomisierten PCA \(O(n_{\max}^2 \cdot n_{\mathrm{components}})\) anstelle von \(O(n_{\max}^2 \cdot n_{\min})\) für die exakte Methode, die in PCA implementiert ist.

Der Speicherbedarf der randomisierten PCA ist ebenfalls proportional zu \(2 \cdot n_{\max} \cdot n_{\mathrm{components}}\) anstelle von \(n_{\max} \cdot n_{\min}\) für die exakte Methode.

Hinweis: Die Implementierung von inverse_transform in PCA mit svd_solver='randomized' ist nicht die exakte inverse Transformation von transform, selbst wenn whiten=False (Standard) ist.

Beispiele

• Gesichtserkennungsbeispiel mit Eigenfaces und SVMs

• Zerlegung von Gesicht-Datensätzen

Referenzen

• Algorithmus 4.3 in „Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions“ Halko, et al., 2009

• „An implementation of a randomized algorithm for principal component analysis“ A. Szlam et al. 2014

2.5.1.4. Sparse Principal Component Analysis (SparsePCA und MiniBatchSparsePCA)

SparsePCA ist eine Variante von PCA mit dem Ziel, die Menge spärlicher Komponenten zu extrahieren, die die Daten am besten rekonstruieren.

Mini-Batch Sparse PCA (MiniBatchSparsePCA) ist eine Variante von SparsePCA, die schneller, aber weniger genau ist. Die erhöhte Geschwindigkeit wird erreicht, indem für eine gegebene Anzahl von Iterationen über kleine Teile der Merkmalmenge iteriert wird.

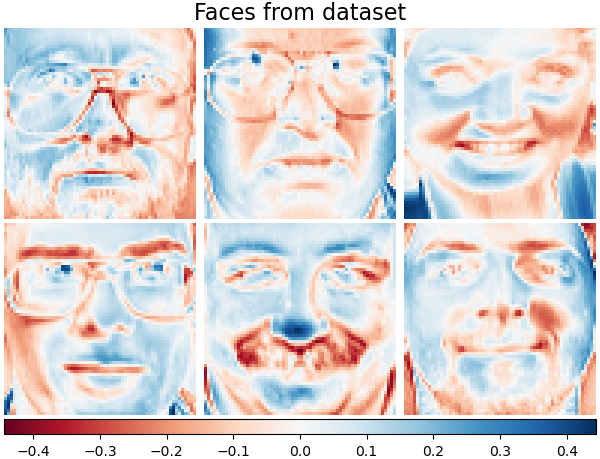
Principal Component Analysis (PCA) hat den Nachteil, dass die mit dieser Methode extrahierten Komponenten ausschließlich dichte Ausdrücke haben, d. h. sie haben Nicht-Null-Koeffizienten, wenn sie als lineare Kombinationen der ursprünglichen Variablen ausgedrückt werden. Dies kann die Interpretation erschweren. In vielen Fällen können die realen zugrunde liegenden Komponenten natürlicher als spärliche Vektoren vorgestellt werden; zum Beispiel bei der Gesichtserkennung könnten Komponenten natürlich Teilen von Gesichtern zugeordnet werden.

Spärliche Hauptkomponenten ergeben eine parsimonischere, interpretierbare Darstellung, die klar hervorhebt, welche der ursprünglichen Merkmale zu den Unterschieden zwischen den Stichproben beitragen.

Das folgende Beispiel illustriert 16 Komponenten, die mit spärlicher PCA aus dem Olivetti-Gesichtsdatensatz extrahiert wurden. Man kann sehen, wie der Regularisierungsterm viele Nullen induziert. Darüber hinaus verursacht die natürliche Struktur der Daten, dass die Nicht-Null-Koeffizienten vertikal nebeneinander liegen. Das Modell erzwingt dies nicht mathematisch: Jede Komponente ist ein Vektor \(h \in \mathbf{R}^{4096}\), und es gibt keinen Begriff der vertikalen Nachbarschaft, außer während der für Menschen lesbaren Visualisierung als 64x64 Pixel-Bilder. Die Tatsache, dass die unten gezeigten Komponenten lokal erscheinen, ist ein Effekt der inhärenten Struktur der Daten, die solche lokalen Muster zur Minimierung des Rekonstruktionsfehlers führen. Es gibt spärlichkeitsinduzierende Normen, die Nachbarschaft und verschiedene Arten von Strukturen berücksichtigen; siehe [Jen09] für eine Übersicht über solche Methoden. Weitere Details zur Verwendung von Sparse PCA finden Sie im Abschnitt Beispiele unten.

Beachten Sie, dass es viele verschiedene Formulierungen für das Sparse PCA-Problem gibt. Die hier implementierte basiert auf [Mrl09]. Das gelöste Optimierungsproblem ist ein PCA-Problem (Dictionary Learning) mit einer \(\ell_1\)-Strafe auf die Komponenten

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||V||_{1,1} \\ \text{subject to } & ||U_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{components}\end{split}\]

\(||.||_{\text{Fro}}\) steht für die Frobenius-Norm und \(||.||_{1,1}\) steht für die eintragweise Matrixnorm, die die Summe der absoluten Werte aller Einträge in der Matrix ist. Die spärlichkeitsinduzierende \(||.||_{1,1}\)-Matrixnorm verhindert auch das Erlernen von Komponenten aus Rauschen, wenn nur wenige Trainingsstichproben verfügbar sind. Der Grad der Bestrafung (und damit der Spärlichkeit) kann über den Hyperparameter alpha angepasst werden. Kleine Werte führen zu einer sanft regularisierten Faktorisierung, während größere Werte viele Koeffizienten auf Null schrumpfen lassen.

Hinweis

Obwohl im Sinne eines Online-Algorithmus, implementiert die Klasse MiniBatchSparsePCA keine partial_fit, da der Algorithmus entlang der Merkmalsrichtung, nicht der Stichprobenrichtung online ist.

Beispiele

• Zerlegung von Gesicht-Datensätzen

Referenzen

[Mrl09]

„Online Dictionary Learning for Sparse Coding“ J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

[Jen09]

„Structured Sparse Principal Component Analysis“ R. Jenatton, G. Obozinski, F. Bach, 2009

2.5.2. Kernel Principal Component Analysis (kPCA)

2.5.2.1. Exakte Kernel-PCA

KernelPCA ist eine Erweiterung von PCA, die eine nichtlineare Dimensionsreduktion durch die Verwendung von Kernels (siehe Paarweise Metriken, Affinitäten und Kerne) erreicht [Scholkopf1997]. Sie hat viele Anwendungen, darunter Rauschunterdrückung, Komprimierung und strukturierte Vorhersage (Schätzung von Kerndependenzen). KernelPCA unterstützt sowohl transform als auch inverse_transform.

Hinweis

KernelPCA.inverse_transform stützt sich auf einen Kernel-Ridge, um die Funktion zu lernen, die Stichproben vom PCA-Basis in den ursprünglichen Merkmalsraum abbildet [Bakir2003]. Daher ist die Rekonstruktion, die mit KernelPCA.inverse_transform erzielt wird, eine Annäherung. Siehe das unten verlinkte Beispiel für weitere Details.

Beispiele

• Kernel PCA

• Bildrauschen mit Kernel PCA

Referenzen

[Scholkopf1997]

Schölkopf, Bernhard, Alexander Smola und Klaus-Robert Müller. „Kernel principal component analysis.“ International conference on artificial neural networks. Springer, Berlin, Heidelberg, 1997.

[Bakir2003]

Bakır, Gökhan H., Jason Weston und Bernhard Schölkopf. „Learning to find pre-images.“ Advances in neural information processing systems 16 (2003): 449-456.

2.5.2.2. Wahl des Lösers für Kernel-PCA

Während bei PCA die Anzahl der Komponenten durch die Anzahl der Merkmale begrenzt ist, ist bei KernelPCA die Anzahl der Komponenten durch die Anzahl der Stichproben begrenzt. Viele reale Datensätze haben eine große Anzahl von Stichproben! In diesen Fällen ist die Suche nach *allen* Komponenten mit einer vollständigen kPCA eine Verschwendung von Rechenzeit, da die Daten hauptsächlich durch die ersten wenigen Komponenten beschrieben werden (z. B. n_components<=100). Mit anderen Worten, die zentrierte Gram-Matrix, die im Kernel-PCA-Anpassungsprozess eigendekomponiert wird, hat einen effektiven Rang, der viel kleiner als ihre Größe ist. Dies ist eine Situation, in der approximative Eigensolver eine Beschleunigung mit sehr geringem Präzisionsverlust bieten können.

Eigensolver

Der optionale Parameter eigen_solver='randomized' kann verwendet werden, um die Berechnungszeit *signifikant* zu reduzieren, wenn die Anzahl der angeforderten n_components klein im Vergleich zur Anzahl der Stichproben ist. Er stützt sich auf randomisierte Zerlegungsverfahren, um in kürzerer Zeit eine ungefähre Lösung zu finden.

Die Zeitkomplexität der randomisierten KernelPCA beträgt \(O(n_{\mathrm{samples}}^2 \cdot n_{\mathrm{components}})\) anstelle von \(O(n_{\mathrm{samples}}^3)\) für die exakte Methode, die mit eigen_solver='dense' implementiert ist.

Der Speicherbedarf der randomisierten KernelPCA ist ebenfalls proportional zu \(2 \cdot n_{\mathrm{samples}} \cdot n_{\mathrm{components}}\) anstelle von \(n_{\mathrm{samples}}^2\) für die exakte Methode.

Hinweis: Diese Technik ist die gleiche wie in PCA mit randomisierter SVD.

Zusätzlich zu den beiden oben genannten Lösungsansätzen kann eigen_solver='arpack' als alternative Möglichkeit zur Erzielung einer ungefähren Zerlegung verwendet werden. In der Praxis liefert diese Methode nur bei extrem wenigen zu findenden Komponenten vernünftige Ausführungszeiten. Sie ist standardmäßig aktiviert, wenn die gewünschte Anzahl von Komponenten kleiner als 10 (strikt) und die Anzahl der Stichproben größer als 200 (strikt) ist. Siehe KernelPCA für Details.

Referenzen

• dense-Solver: Dokumentation zu scipy.linalg.eigh

• randomized-Solver

  • Algorithmus 4.3 in „Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions“ Halko, et al. (2009)

  • „An implementation of a randomized algorithm for principal component analysis“ A. Szlam et al. (2014)

• arpack-Solver: Dokumentation zu scipy.sparse.linalg.eigsh R. B. Lehoucq, D. C. Sorensen und C. Yang, (1998)

2.5.3. Abgeschnittene Singulärwertzerlegung und Latent Semantic Analysis

TruncatedSVD implementiert eine Variante der Singulärwertzerlegung (SVD), die nur die \(k\) größten Singulärwerte berechnet, wobei \(k\) ein benutzerdefinierter Parameter ist.

TruncatedSVD ist der PCA sehr ähnlich, unterscheidet sich jedoch dadurch, dass die Matrix \(X\) nicht zentriert sein muss. Wenn von den Merkmalwerten die spaltenweisen (pro Merkmal) Mittelwerte von \(X\) subtrahiert werden, ist die abgeschnittene SVD der resultierenden Matrix äquivalent zu PCA.

Über abgeschnittene SVD und Latent Semantic Analysis (LSA)

Wenn die abgeschnittene SVD auf Term-Dokument-Matrizen (wie sie von CountVectorizer oder TfidfVectorizer zurückgegeben werden) angewendet wird, wird diese Transformation als Latent Semantic Analysis (LSA) bezeichnet, da sie solche Matrizen in einen „semantischen“ Raum niedriger Dimensionalität transformiert. Insbesondere ist bekannt, dass LSA die Auswirkungen von Synonymie und Polysemie (die beide grob bedeuten, dass es mehrere Bedeutungen pro Wort gibt) bekämpft, die Term-Dokument-Matrizen übermäßig spärlich machen und unter Maßnahmen wie der Kosinus-Ähnlichkeit schlecht abschneiden.

Hinweis

LSA ist auch als Latent Semantic Indexing, LSI, bekannt, obwohl sich dies streng genommen auf seine Verwendung in persistenten Indizes für Informationsabfragezwecke bezieht.

Mathematisch erzeugt die abgeschnittene SVD, die auf Trainingsstichproben \(X\) angewendet wird, eine Niedrigrang-Annäherung \(X\)

\[X \approx X_k = U_k \Sigma_k V_k^\top\]

Nach dieser Operation ist \(U_k \Sigma_k\) die transformierte Trainingsmenge mit \(k\) Merkmalen (genannt n_components in der API).

Um auch eine Testmenge \(X\) zu transformieren, multiplizieren wir sie mit \(V_k\)

\[X' = X V_k\]

Hinweis

Die meisten Behandlungen von LSA in der natürlichen Sprachverarbeitung (NLP) und Informationsabfrage (IR) Literatur vertauschen die Achsen der Matrix \(X\), sodass sie die Form (n_features, n_samples) hat. Wir präsentieren LSA auf eine andere Weise, die besser zur scikit-learn API passt, aber die gefundenen singulären Werte sind dieselben.

Während der TruncatedSVD Transformer mit jeder Merkmalsmatrix funktioniert, wird seine Verwendung auf TF-IDF-Matrizen gegenüber rohen Häufigkeitszählungen in einem LSA/Dokumentenverarbeitungsszenario empfohlen. Insbesondere sollten sublineare Skalierung und Inverse Document Frequency eingeschaltet werden (sublinear_tf=True, use_idf=True), um die Merkmalswerte näher an eine Gaußsche Verteilung zu bringen und die fehlerhaften Annahmen von LSA über Textdaten auszugleichen.

Beispiele

• Clustering von Textdokumenten mit K-Means

Referenzen

• Christopher D. Manning, Prabhakar Raghavan und Hinrich Schütze (2008), Introduction to Information Retrieval, Cambridge University Press, Kapitel 18: Matrix decompositions & latent semantic indexing

2.5.4. Dictionary Learning

2.5.4.1. Sparse Coding mit einem vortrainierten Dictionary

Das Objekt SparseCoder ist ein Schätzer, der verwendet werden kann, um Signale in spärliche lineare Kombinationen von Atomen aus einem festen, vortrainierten Dictionary wie einer diskreten Wavelet-Basis zu transformieren. Dieses Objekt implementiert daher keine fit-Methode. Die Transformation entspricht einem Sparse-Coding-Problem: ein Datensatz wird als lineare Kombination von möglichst wenigen Dictionary-Atomen dargestellt.

• Orthogonal Matching Pursuit (Orthogonal Matching Pursuit (OMP))

• Least-Angle Regression (Least Angle Regression)

• Lasso berechnet mittels Least-Angle Regression

• Lasso mit Coordinate Descent (Lasso)

• Thresholding

Thresholding ist sehr schnell, liefert aber keine genauen Rekonstruktionen. Es hat sich in der Literatur für Klassifizierungsaufgaben als nützlich erwiesen. Für Bildrekonstruktionsaufgaben liefert Orthogonal Matching Pursuit die genaueste, unverzerrteste Rekonstruktion.

Die Dictionary-Learning-Objekte bieten über den Parameter split_code die Möglichkeit, die positiven und negativen Werte in den Ergebnissen des Sparse Coding zu trennen. Dies ist nützlich, wenn Dictionary Learning zur Extraktion von Merkmalen für überwachtes Lernen verwendet wird, da es dem Lernalgorithmus ermöglicht, verschiedenen Gewichten für negative Lasten eines bestimmten Atoms zuzuweisen als den entsprechenden positiven Lasten.

Der geteilte Code für eine einzelne Stichprobe hat eine Länge von 2 * n_components und wird nach folgender Regel erstellt: Zuerst wird der reguläre Code der Länge n_components berechnet. Dann werden die ersten n_components Einträge des split_code mit dem positiven Teil des regulären Codevektors gefüllt. Die zweite Hälfte des geteilten Codes wird mit dem negativen Teil des Codevektors gefüllt, nur mit positivem Vorzeichen. Daher ist der split_code nicht negativ.

Beispiele

• Sparse Coding mit einem voreingestellten Dictionary

2.5.4.2. Allgemeines Dictionary Learning

Dictionary Learning (DictionaryLearning) ist ein Matrixfaktorisierungsproblem, das darin besteht, ein (normalerweise übervollständiges) Dictionary zu finden, das gut darin ist, die angepassten Daten spärlich zu kodieren.

Die Darstellung von Daten als spärliche Kombinationen von Atomen aus einem übervollständigen Dictionary wird als Arbeitsweise des primären visuellen Kortex von Säugetieren vorgeschlagen. Folglich hat Dictionary Learning, das auf Bild-Patches angewendet wird, gute Ergebnisse bei Bildverarbeitungsaufgaben wie Bildvervollständigung, Inpainting und Rauschunterdrückung erzielt, sowie für überwachungsbasierte Erkennungsaufgaben.

Dictionary Learning ist ein Optimierungsproblem, das durch abwechselndes Aktualisieren des spärlichen Codes, als Lösung mehrerer Lasso-Probleme bei festem Dictionary, und dann durch Aktualisieren des Dictionarys gelöst wird, um den spärlichen Code am besten anzupassen.

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||U||_{1,1} \\ \text{subject to } & ||V_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{\mathrm{atoms}}\end{split}\]

\(||.||_{\text{Fro}}\) steht für die Frobenius-Norm und \(||.||_{1,1}\) steht für die eintragweise Matrixnorm, die die Summe der absoluten Werte aller Einträge in der Matrix ist. Nach der Verwendung eines solchen Verfahrens zur Anpassung des Dictionarys ist die Transformation einfach ein Sparse-Coding-Schritt, der die gleiche Implementierung wie alle Dictionary-Learning-Objekte teilt (siehe Sparse Coding mit einem vortrainierten Dictionary).

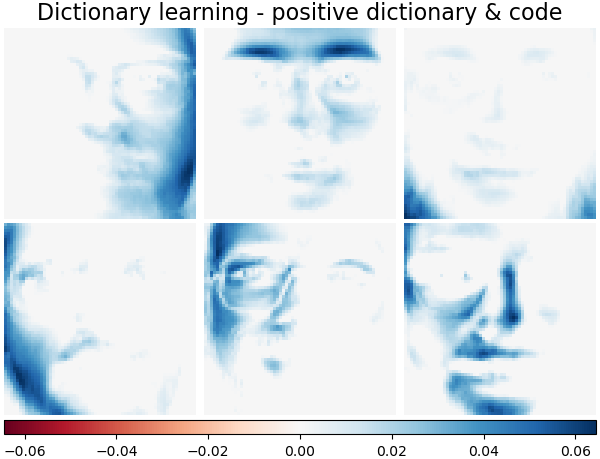
Es ist auch möglich, das Dictionary und/oder den Code auf positiv zu beschränken, um Einschränkungen abzugleichen, die möglicherweise in den Daten vorhanden sind. Unten sind die Gesichter mit verschiedenen Positivitätseinschränkungen dargestellt. Rot bedeutet negative Werte, Blau bedeutet positive Werte und Weiß bedeutet Nullen.

Referenzen

• „Online dictionary learning for sparse coding“ J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

2.5.4.3. Mini-Batch Dictionary Learning

MiniBatchDictionaryLearning implementiert eine schnellere, aber weniger genaue Version des Dictionary-Learning-Algorithmus, die sich besser für große Datensätze eignet.

Standardmäßig teilt MiniBatchDictionaryLearning die Daten in Mini-Batches auf und optimiert online, indem es für die angegebene Anzahl von Iterationen über die Mini-Batches zyklisch durchläuft. Derzeit implementiert es jedoch keine Stoppbedingung.

Der Schätzer implementiert auch partial_fit, das das Dictionary aktualisiert, indem es nur einmal über einen Mini-Batch iteriert. Dies kann für das Online-Lernen verwendet werden, wenn die Daten nicht von Anfang an verfügbar sind oder wenn die Daten nicht in den Speicher passen.

Clustering für Dictionary Learning

Beachten Sie, dass beim Verwenden von Dictionary Learning zur Extraktion einer Darstellung (z. B. für Sparse Coding) Clustering ein guter Stellvertreter sein kann, um das Dictionary zu lernen. Zum Beispiel ist der Schätzer MiniBatchKMeans rechnerisch effizient und implementiert Online-Lernen mit einer partial_fit-Methode.

Beispiel: Online-Lernen eines Dictionaries von Teilen von Gesichtern

Das folgende Bild zeigt, wie ein Dictionary, das aus 4x4 Pixel-Bild-Patches aus einem Teil des Bildes eines Waschbärgesichts gelernt wurde, aussieht.

Beispiele

• Bildrauschen mit Dictionary Learning

2.5.5. Faktoranalyse

Im unüberwachten Lernen haben wir nur einen Datensatz \(X = \{x_1, x_2, \dots, x_n \}\). Wie kann dieser Datensatz mathematisch beschrieben werden? Ein sehr einfaches kontinuierliches latentes Variablenmodell für \(X\) ist

\[x_i = W h_i + \mu + \epsilon\]

Der Vektor \(h_i\) wird als „latent“ bezeichnet, weil er unbeobachtet ist. \(\epsilon\) wird als Rauschterm betrachtet, der nach einer Gaußschen Verteilung mit Mittelwert 0 und Kovarianz \(\Psi\) verteilt ist (d. h. \(\epsilon \sim \mathcal{N}(0, \Psi)\)), \(\mu\) ist ein beliebiger Offset-Vektor. Ein solches Modell wird als „generativ“ bezeichnet, da es beschreibt, wie \(x_i\) aus \(h_i\) generiert wird. Wenn wir alle \(x_i\) als Spalten verwenden, um eine Matrix \(\mathbf{X}\) zu bilden, und alle \(h_i\) als Spalten einer Matrix \(\mathbf{H}\), dann können wir schreiben (mit geeignet definierten \(\mathbf{M}\) und \(\mathbf{E}\))

\[\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}\]

Mit anderen Worten, wir haben die Matrix \(\mathbf{X}\) zerlegt.

Wenn \(h_i\) gegeben ist, impliziert die obige Gleichung automatisch die folgende probabilistische Interpretation

\[p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)\]

Für ein vollständiges probabilistisches Modell benötigen wir auch eine Prior-Verteilung für die latente Variable \(h\). Die naheliegendste Annahme (basierend auf den guten Eigenschaften der Gaußschen Verteilung) ist \(h \sim \mathcal{N}(0, \mathbf{I})\). Dies ergibt eine Gaußsche Verteilung als Randverteilung von \(x\)

\[p(x) = \mathcal{N}(\mu, WW^T + \Psi)\]

Nun, ohne weitere Annahmen, wäre die Idee, eine latente Variable \(h\) zu haben, überflüssig – \(x\) kann vollständig mit einem Mittelwert und einer Kovarianz modelliert werden. Wir müssen einigen dieser beiden Parameter eine spezifischere Struktur aufzwingen. Eine einfache zusätzliche Annahme betrifft die Struktur der Fehlerkovarianz \(\Psi\)

• \(\Psi = \sigma^2 \mathbf{I}\): Diese Annahme führt zum probabilistischen Modell von PCA.

• \(\Psi = \mathrm{diag}(\psi_1, \psi_2, \dots, \psi_n)\): Dieses Modell wird als FactorAnalysis bezeichnet, ein klassisches statistisches Modell. Die Matrix W wird manchmal als „Faktorladungsmatrix“ bezeichnet.

Beide Modelle schätzen im Wesentlichen eine Gaußsche Verteilung mit einer niedrigrangigen Kovarianzmatrix. Da beide Modelle probabilistisch sind, können sie in komplexere Modelle integriert werden, z. B. Mixture of Factor Analysers. Man erhält sehr unterschiedliche Modelle (z. B. FastICA), wenn nicht-Gaußsche Prioren auf die latenten Variablen angenommen werden.

Faktorenanalyse kann ähnliche Komponenten (die Spalten ihrer Ladungsmatrix) wie PCA erzeugen. Es können jedoch keine allgemeinen Aussagen über diese Komponenten getroffen werden (z. B. ob sie orthogonal sind).

Der Hauptvorteil der Faktorenanalyse gegenüber PCA ist, dass sie die Varianz in jeder Richtung des Eingangsraums unabhängig modellieren kann (heteroskedastisches Rauschen).

Dies ermöglicht eine bessere Modellauswahl als probabilistische PCA bei Vorhandensein von heteroskedastischem Rauschen.

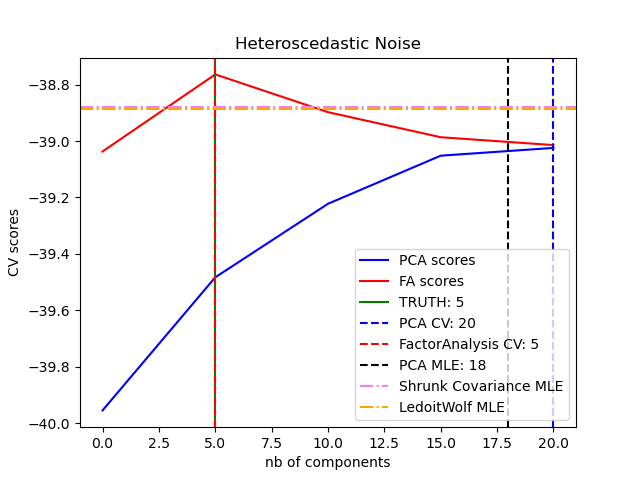
Faktorenanalyse wird oft von einer Rotation der Faktoren (mit dem Parameter rotation) gefolgt, üblicherweise um die Interpretierbarkeit zu verbessern. Zum Beispiel maximiert die Varimax-Rotation die Summe der Varianzen der quadrierten Ladungen, d.h. sie tendiert dazu, spärlichere Faktoren zu erzeugen, die nur von wenigen Merkmalen beeinflusst werden (die „einfache Struktur“). Siehe z.B. das erste Beispiel unten.

Beispiele

• Faktorenanalyse (mit Rotation) zur Visualisierung von Mustern

• Modellauswahl mit Probabilistischem PCA und Faktorenanalyse (FA)

2.5.6. Independent Component Analysis (ICA)

Independent Component Analysis trennt ein multivariates Signal in additive Unterkomponenten, die maximal unabhängig sind. Sie wird in scikit-learn mit dem Algorithmus Fast ICA implementiert. Typischerweise wird ICA nicht zur Dimensionsreduktion verwendet, sondern zur Trennung überlagerter Signale. Da das ICA-Modell keinen Rauschterm enthält, muss für ein korrektes Modell eine Entrauschung (Whitening) angewendet werden. Dies kann intern über das Argument whiten oder manuell über eine der PCA-Varianten erfolgen.

Sie wird klassischerweise zur Trennung gemischter Signale verwendet (ein Problem, das als Blind Source Separation bekannt ist), wie im folgenden Beispiel

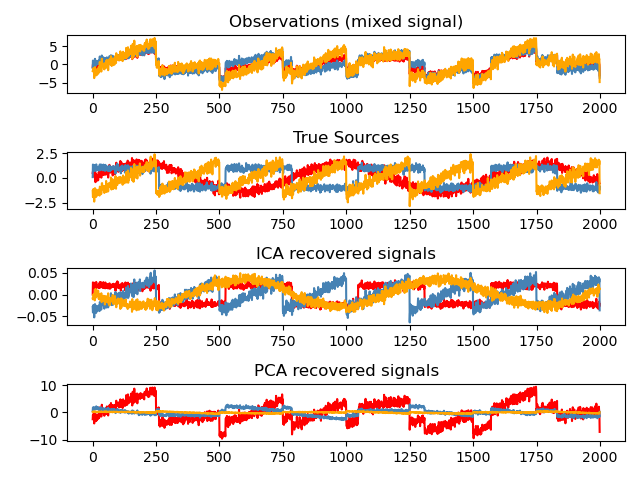
ICA kann auch als eine weitere nicht-lineare Zerlegung verwendet werden, die Komponenten mit gewisser Sparsity findet.

Beispiele

• Blind Source Separation mit FastICA

• FastICA auf 2D Punktwolken

• Zerlegung von Gesicht-Datensätzen

2.5.7. Non-negative Matrix Factorization (NMF oder NNMF)

2.5.7.1. NMF mit der Frobenius-Norm

NMF [1] ist ein alternativer Ansatz zur Zerlegung, der annimmt, dass die Daten und die Komponenten nicht-negativ sind. NMF kann anstelle von PCA oder seinen Varianten verwendet werden, wenn die Datenmatrix keine negativen Werte enthält. Sie findet eine Zerlegung von Stichproben \(X\) in zwei Matrizen \(W\) und \(H\) mit nicht-negativen Elementen, indem der Abstand \(d\) zwischen \(X\) und dem Matrixprodukt \(WH\) optimiert wird. Die am weitesten verbreitete Distanzfunktion ist die quadrierte Frobenius-Norm, die eine offensichtliche Erweiterung der euklidischen Norm auf Matrizen ist.

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

Im Gegensatz zu PCA wird die Darstellung eines Vektors additiv durch Überlagerung der Komponenten erhalten, ohne Subtraktion. Solche additiven Modelle sind effizient für die Darstellung von Bildern und Texten.

Es wurde in [Hoyer, 2004] [2] beobachtet, dass NMF bei sorgfältiger Einschränkung eine „parts-based“ Darstellung des Datensatzes erzeugen kann, was zu interpretierbaren Modellen führt. Das folgende Beispiel zeigt 16 spärliche Komponenten, die von NMF aus den Bildern des Olivetti-Gesichterdatensatzes gefunden wurden, im Vergleich zu den PCA-Eigenfaces.

Das Attribut init bestimmt die angewendete Initialisierungsmethode, die einen großen Einfluss auf die Leistung der Methode hat. NMF implementiert die Methode Nonnegative Double Singular Value Decomposition. NNDSVD [4] basiert auf zwei SVD-Prozessen: einem, der die Datenmatrix annähert, und einem, der positive Abschnitte der resultierenden partiellen SVD-Faktoren unter Ausnutzung einer algebraischen Eigenschaft von Einheitsrangmatrizen annähert. Der grundlegende NNDSVD-Algorithmus ist besser für spärliche Faktorisierungen geeignet. Seine Varianten NNDSVDa (bei der alle Nullen gleich dem Mittelwert aller Elemente der Daten gesetzt werden) und NNDSVDar (bei der die Nullen mit zufälligen Störungen kleiner als der Mittelwert der Daten geteilt durch 100 gesetzt werden) werden im dichten Fall empfohlen.

Beachten Sie, dass der Multiplicative Update (‘mu’)-Solver Nullen in der Initialisierung nicht aktualisieren kann, was zu schlechteren Ergebnissen führt, wenn er zusammen mit dem grundlegenden NNDSVD-Algorithmus verwendet wird, der viele Nullen erzeugt; in diesem Fall sollten NNDSVDa oder NNDSVDar bevorzugt werden.

NMF kann auch mit korrekt skalierten zufälligen nicht-negativen Matrizen initialisiert werden, indem init="random" gesetzt wird. Ein Ganzzahlsamen oder ein RandomState kann ebenfalls an random_state übergeben werden, um die Reproduzierbarkeit zu steuern.

In NMF können L1- und L2-Priors zur Verlustfunktion hinzugefügt werden, um das Modell zu regularisieren. Der L2-Prior verwendet die Frobenius-Norm, während der L1-Prior eine elementweise L1-Norm verwendet. Wie bei ElasticNet steuern wir die Kombination von L1 und L2 mit dem Parameter l1_ratio (\(\rho\)) und die Intensität der Regularisierung mit den Parametern alpha_W und alpha_H (\(\alpha_W\) und \(\alpha_H\)). Die Prioren werden durch die Anzahl der Stichproben (\(n\_samples\)) für H und die Anzahl der Merkmale (\(n\_features\)) für W skaliert, um ihre Auswirkung im Verhältnis zueinander und zum Datenanpassungs-Term so unabhängig wie möglich von der Größe der Trainingsmenge zu halten. Dann sind die Prior-Terme

\[(\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

und die regularisierte Zielfunktion ist

\[d_{\mathrm{Fro}}(X, WH) + (\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

2.5.7.2. NMF mit einer Beta-Divergenz

Wie bereits beschrieben, ist die am weitesten verbreitete Distanzfunktion die quadrierte Frobenius-Norm, die eine offensichtliche Erweiterung der euklidischen Norm auf Matrizen ist.

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{Fro}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

Andere Distanzfunktionen können in NMF verwendet werden, wie z. B. die (generalisierte) Kullback-Leibler (KL)-Divergenz, auch als I-Divergenz bezeichnet.

\[d_{KL}(X, Y) = \sum_{i,j} (X_{ij} \log(\frac{X_{ij}}{Y_{ij}}) - X_{ij} + Y_{ij})\]

Oder die Itakura-Saito (IS)-Divergenz.

\[d_{IS}(X, Y) = \sum_{i,j} (\frac{X_{ij}}{Y_{ij}} - \log(\frac{X_{ij}}{Y_{ij}}) - 1)\]

Diese drei Distanzen sind Sonderfälle der Beta-Divergenz-Familie, mit \(\beta = 2, 1, 0\) bzw. [6]. Die Beta-Divergenz ist definiert durch

\[d_{\beta}(X, Y) = \sum_{i,j} \frac{1}{\beta(\beta - 1)}(X_{ij}^\beta + (\beta-1)Y_{ij}^\beta - \beta X_{ij} Y_{ij}^{\beta - 1})\]

Beachten Sie, dass diese Definition nicht gültig ist, wenn \(\beta \in (0; 1)\), sie kann jedoch kontinuierlich auf die Definitionen von \(d_{KL}\) und \(d_{IS}\) erweitert werden.

Implementierte NMF-Solver

NMF implementiert zwei Solver: Coordinate Descent (‘cd’) [5] und Multiplicative Update (‘mu’) [6]. Der ‚mu‘-Solver kann jede Beta-Divergenz optimieren, einschließlich der Frobenius-Norm (\(\beta=2\)), der (generalisierte) Kullback-Leibler-Divergenz (\(\beta=1\)) und der Itakura-Saito-Divergenz (\(\beta=0\)). Beachten Sie, dass für \(\beta \in (1; 2)\) der ‚mu‘-Solver erheblich schneller ist als für andere Werte von \(\beta\). Beachten Sie auch, dass bei einem negativen (oder 0, d.h. ‚itakura-saito‘) \(\beta\) die Eingangsmatrix keine Nullwerte enthalten darf.

Der ‚cd‘-Solver kann nur die Frobenius-Norm optimieren. Aufgrund der zugrunde liegenden Nichtkonvexität von NMF können die verschiedenen Solver unterschiedliche Minima konvergieren, auch wenn sie dieselbe Distanzfunktion optimieren.

NMF wird am besten mit der Methode fit_transform verwendet, die die Matrix W zurückgibt. Die Matrix H wird im angepassten Modell im Attribut components_ gespeichert; die Methode transform zerlegt eine neue Matrix X_new basierend auf diesen gespeicherten Komponenten.

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)

Beispiele

• Zerlegung von Gesicht-Datensätzen

• Themenextraktion mit Non-negative Matrix Factorization und Latent Dirichlet Allocation

2.5.7.3. Mini-Batch Non-Negative Matrix Factorization

MiniBatchNMF [7] implementiert eine schnellere, aber weniger genaue Version der nicht-negativen Matrixfaktorisierung (d.h. NMF), die besser für große Datensätze geeignet ist.

Standardmäßig teilt MiniBatchNMF die Daten in Mini-Batches auf und optimiert das NMF-Modell online, indem es für die angegebene Anzahl von Iterationen über die Mini-Batches zyklisch durchläuft. Der Parameter batch_size steuert die Größe der Batches.

Um den Mini-Batch-Algorithmus zu beschleunigen, ist es auch möglich, vergangene Batches zu skalieren und ihnen weniger Bedeutung als neueren Batches zu geben. Dies geschieht durch die Einführung eines sogenannten Vergessensfaktors, der durch den Parameter forget_factor gesteuert wird.

Der Schätzer implementiert auch partial_fit, das H aktualisiert, indem es nur einmal über einen Mini-Batch iteriert. Dies kann für Online-Lernen verwendet werden, wenn die Daten nicht von Anfang an verfügbar sind oder wenn die Daten nicht in den Speicher passen.

Referenzen

[1]

“Learning the parts of objects by non-negative matrix factorization” D. Lee, S. Seung, 1999

[2]

“Non-negative Matrix Factorization with Sparseness Constraints” P. Hoyer, 2004

[4]

“SVD based initialization: A head start for nonnegative matrix factorization” C. Boutsidis, E. Gallopoulos, 2008

[5]

“Fast local algorithms for large scale nonnegative matrix and tensor factorizations.” A. Cichocki, A. Phan, 2009

[6] (1,2)

“Algorithms for nonnegative matrix factorization with the beta-divergence” C. Fevotte, J. Idier, 2011

[7]

“Online algorithms for nonnegative matrix factorization with the Itakura-Saito divergence” A. Lefevre, F. Bach, C. Fevotte, 2011

2.5.8. Latent Dirichlet Allocation (LDA)

Latent Dirichlet Allocation ist ein generatives probabilistisches Modell für Sammlungen diskreter Datensätze wie Textkorpora. Es ist auch ein Topic-Modell, das zur Entdeckung abstrakter Themen aus einer Sammlung von Dokumenten verwendet wird.

Das grafische Modell von LDA ist ein dreistufiges generatives Modell.

Hinweis zu den in obigem grafischen Modell dargestellten Notationen, die in Hoffman et al. (2013) zu finden sind.

• Der Korpus ist eine Sammlung von \(D\) Dokumenten.

• Ein Dokument \(d \in D\) ist eine Sequenz von \(N_d\) Wörtern.

• Es gibt \(K\) Themen im Korpus.

• Die Kästen stellen wiederholte Stichproben dar.

Im grafischen Modell ist jeder Knoten eine Zufallsvariable und spielt eine Rolle im generativen Prozess. Ein schattierter Knoten kennzeichnet eine beobachtete Variable und ein unschattierter Knoten eine versteckte (latente) Variable. In diesem Fall sind die Wörter im Korpus die einzigen Daten, die wir beobachten. Die latenten Variablen bestimmen die zufällige Mischung von Themen im Korpus und die Verteilung der Wörter in den Dokumenten. Ziel von LDA ist es, die beobachteten Wörter zur Inferenz der versteckten Themenstruktur zu verwenden.

Details zur Modellierung von Textkorpora

Bei der Modellierung von Textkorpora nimmt das Modell den folgenden generativen Prozess für einen Korpus mit \(D\) Dokumenten und \(K\) Themen an, wobei \(K\) n_components in der API entspricht.

1. Für jedes Thema \(k \in K\), ziehe \(\beta_k \sim \mathrm{Dirichlet}(\eta)\). Dies liefert eine Verteilung über die Wörter, d. h. die Wahrscheinlichkeit eines Wortes, in Thema \(k\) zu erscheinen. \(\eta\) entspricht topic_word_prior.

2. Für jedes Dokument \(d \in D\), ziehe die Themenanteile \(\theta_d \sim \mathrm{Dirichlet}(\alpha)\). \(\alpha\) entspricht doc_topic_prior.

3. Für jedes Wort \(n=1,\cdots,N_d\) in Dokument \(d\)

   1. Ziehe die Themenzuweisung \(z_{dn} \sim \mathrm{Multinomial} (\theta_d)\)

   2. Ziehe das beobachtete Wort \(w_{dn} \sim \mathrm{Multinomial} (\beta_{z_{dn}})\)

Für die Parameterschätzung ist die Posterior-Verteilung

\[p(z, \theta, \beta |w, \alpha, \eta) = \frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}\]

Da die Posterior-Verteilung intractable ist, verwendet die variations-bayessche Methode eine einfachere Verteilung \(q(z,\theta,\beta | \lambda, \phi, \gamma)\), um sie zu approximieren, und diese Variationsparameter \(\lambda\), \(\phi\), \(\gamma\) werden optimiert, um die Evidence Lower Bound (ELBO) zu maximieren.

\[\log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=} E_{q}[\log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[\log\:q(z, \theta, \beta)]\]

Die Maximierung der ELBO ist äquivalent zur Minimierung der Kullback-Leibler (KL)-Divergenz zwischen \(q(z,\theta,\beta)\) und der wahren Posterior-Verteilung \(p(z, \theta, \beta |w, \alpha, \eta)\).

LatentDirichletAllocation implementiert den Online-Variations-Bayes-Algorithmus und unterstützt sowohl Online- als auch Batch-Update-Methoden. Während die Batch-Methode die Variationsvariablen nach jedem vollständigen Durchlauf durch die Daten aktualisiert, aktualisiert die Online-Methode die Variationsvariablen aus Mini-Batch-Datenpunkten.

Hinweis

Obwohl die Online-Methode garantiert zu einem lokalen Optimum konvergiert, können die Qualität des Optimums und die Konvergenzgeschwindigkeit von der Mini-Batch-Größe und den Attributen im Zusammenhang mit der Einstellung der Lernrate abhängen.

Wenn LatentDirichletAllocation auf eine „Dokument-Term“-Matrix angewendet wird, wird die Matrix in eine „Themen-Term“-Matrix und eine „Dokument-Themen“-Matrix zerlegt. Während die „Themen-Term“-Matrix als components_ im Modell gespeichert wird, kann die „Dokument-Themen“-Matrix über die transform-Methode berechnet werden.

LatentDirichletAllocation implementiert auch die Methode partial_fit. Diese wird verwendet, wenn Daten sequenziell abgerufen werden können.

Beispiele

• Themenextraktion mit Non-negative Matrix Factorization und Latent Dirichlet Allocation

Referenzen

• “Latent Dirichlet Allocation” D. Blei, A. Ng, M. Jordan, 2003

• “Online Learning for Latent Dirichlet Allocation” M. Hoffman, D. Blei, F. Bach, 2010

• “Stochastic Variational Inference” M. Hoffman, D. Blei, C. Wang, J. Paisley, 2013

• “The varimax criterion for analytic rotation in factor analysis” H. F. Kaiser, 1958

Siehe auch Dimensionsreduktion für Dimensionsreduktion mit Neighborhood Components Analysis.