Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Blind Source Separation mit FastICA#
Ein Beispiel für die Schätzung von Quellen aus verrauschten Daten.
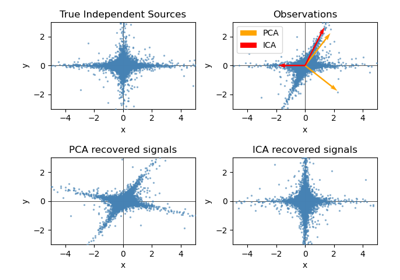
Independent Component Analysis (ICA) wird verwendet, um Quellen anhand verrauschter Messungen zu schätzen. Stellen Sie sich 3 Instrumente vor, die gleichzeitig spielen, und 3 Mikrofone, die die gemischten Signale aufzeichnen. ICA wird verwendet, um die Quellen wiederherzustellen, d. h. was von jedem Instrument gespielt wird. Wichtig ist, dass PCA unsere instruments nicht wiederherstellen kann, da die zugehörigen Signale nicht-gaußsche Prozesse widerspiegeln.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Beispieldaten generieren#
import numpy as np
from scipy import signal
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)
s1 = np.sin(2 * time) # Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time)) # Signal 2 : square signal
s3 = signal.sawtooth(2 * np.pi * time) # Signal 3: saw tooth signal
S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape) # Add noise
S /= S.std(axis=0) # Standardize data
# Mix data
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # Mixing matrix
X = np.dot(S, A.T) # Generate observations
ICA- und PCA-Modelle anpassen#
from sklearn.decomposition import PCA, FastICA
# Compute ICA
ica = FastICA(n_components=3, whiten="arbitrary-variance")
S_ = ica.fit_transform(X) # Reconstruct signals
A_ = ica.mixing_ # Get estimated mixing matrix
# We can `prove` that the ICA model applies by reverting the unmixing.
assert np.allclose(X, np.dot(S_, A_.T) + ica.mean_)
# For comparison, compute PCA
pca = PCA(n_components=3)
H = pca.fit_transform(X) # Reconstruct signals based on orthogonal components
Ergebnisse plotten#
import matplotlib.pyplot as plt
plt.figure()
models = [X, S, S_, H]
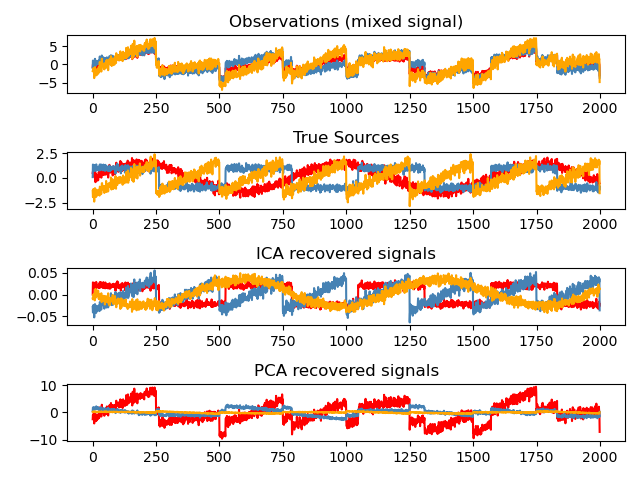
names = [
"Observations (mixed signal)",
"True Sources",
"ICA recovered signals",
"PCA recovered signals",
]
colors = ["red", "steelblue", "orange"]
for ii, (model, name) in enumerate(zip(models, names), 1):
plt.subplot(4, 1, ii)
plt.title(name)
for sig, color in zip(model.T, colors):
plt.plot(sig, color=color)
plt.tight_layout()
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,342 Sekunden)
Verwandte Beispiele
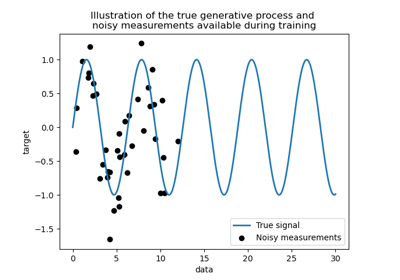
Vergleich von Kernel Ridge und Gauß-Prozess-Regression
Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels