Die Johnson-Lindenstrauss-Schranke für Einbettungen mit Zufallsprojektionen

Das Johnson-Lindenstrauss-Lemma besagt, dass jeder hochdimensionale Datensatz zufällig in einen niedrigdimensionalen euklidischen Raum projiziert werden kann, während die Verzerrung der paarweisen Abstände kontrolliert wird.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import sys
from time import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_20newsgroups_vectorized, load_digits
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.random_projection import (
    SparseRandomProjection,
    johnson_lindenstrauss_min_dim,
)

Theoretische Schranken

Die durch eine Zufallsprojektion p eingeführte Verzerrung wird durch die Tatsache behauptet, dass p mit guter Wahrscheinlichkeit eine Eps-Einbettung definiert, wie sie durch

\[(1 - eps) \|u - v\|^2 < \|p(u) - p(v)\|^2 < (1 + eps) \|u - v\|^2\]

definiert ist. Hierbei sind u und v beliebige Zeilen aus einem Datensatz der Form (n_samples, n_features) und p ist eine Projektion durch eine zufällige Gaußsche N(0, 1)-Matrix der Form (n_components, n_features) (oder eine sparse Achlioptas-Matrix).

Die minimale Anzahl von Komponenten, die die Eps-Einbettung garantiert, ist gegeben durch

\[n\_components \geq 4 log(n\_samples) / (eps^2 / 2 - eps^3 / 3)\]

Der erste Plot zeigt, dass mit steigender Anzahl von Samples n_samples die minimale Anzahl von Dimensionen n_components logarithmisch ansteigt, um eine eps-Einbettung zu garantieren.

# range of admissible distortions
eps_range = np.linspace(0.1, 0.99, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(eps_range)))

# range of number of samples (observation) to embed
n_samples_range = np.logspace(1, 9, 9)

plt.figure()
for eps, color in zip(eps_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples_range, eps=eps)
    plt.loglog(n_samples_range, min_n_components, color=color)

plt.legend([f"eps = {eps:0.1f}" for eps in eps_range], loc="lower right")
plt.xlabel("Number of observations to eps-embed")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_samples vs n_components")
plt.show()

Der zweite Plot zeigt, dass eine Erhöhung der zulässigen Verzerrung eps es ermöglicht, die minimale Anzahl von Dimensionen n_components für eine gegebene Anzahl von Samples n_samples drastisch zu reduzieren.

# range of admissible distortions
eps_range = np.linspace(0.01, 0.99, 100)

# range of number of samples (observation) to embed
n_samples_range = np.logspace(2, 6, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(n_samples_range)))

plt.figure()
for n_samples, color in zip(n_samples_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples, eps=eps_range)
    plt.semilogy(eps_range, min_n_components, color=color)

plt.legend([f"n_samples = {n}" for n in n_samples_range], loc="upper right")
plt.xlabel("Distortion eps")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_components vs eps")
plt.show()

Empirische Validierung

Wir validieren die obigen Schranken auf dem 20-newsgroups-Textdatensatz (TF-IDF-Worthäufigkeiten) oder auf dem digits-Datensatz.

• Für den 20-newsgroups-Datensatz werden etwa 300 Dokumente mit insgesamt 100.000 Merkmalen mithilfe einer spärlichen Zufallsmatrix in kleinere euklidische Räume mit verschiedenen Werten für die Zielanzahl von Dimensionen n_components projiziert.

• Für den digits-Datensatz werden etwa 300 handgeschriebene Ziffernbilder mit Graustufenpixeln der Größe 8x8 in Räume mit verschiedenen größeren Anzahlen von Dimensionen n_components projiziert.

Der Standarddatensatz ist der 20-newsgroups-Datensatz. Um das Beispiel auf dem digits-Datensatz auszuführen, übergeben Sie das Kommandozeilenargument --use-digits-dataset an dieses Skript.

if "--use-digits-dataset" in sys.argv:
    data = load_digits().data[:300]
else:
    data = fetch_20newsgroups_vectorized().data[:300]

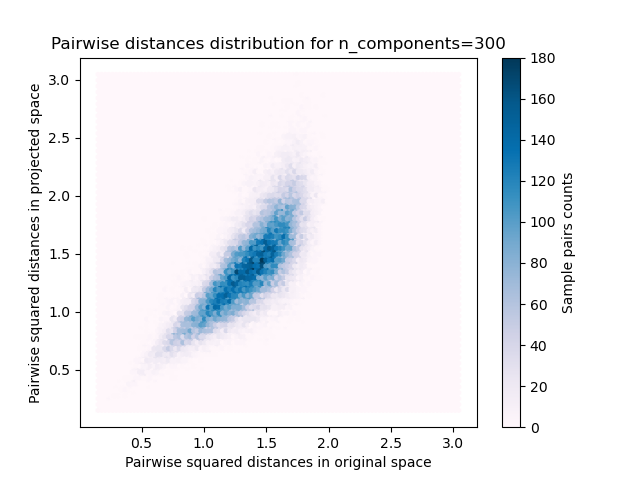
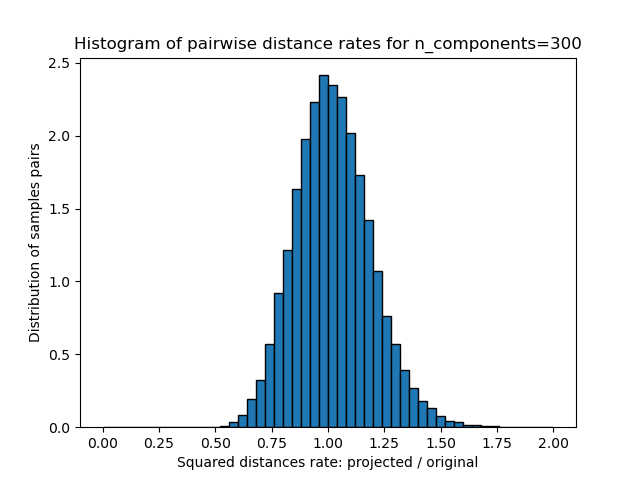
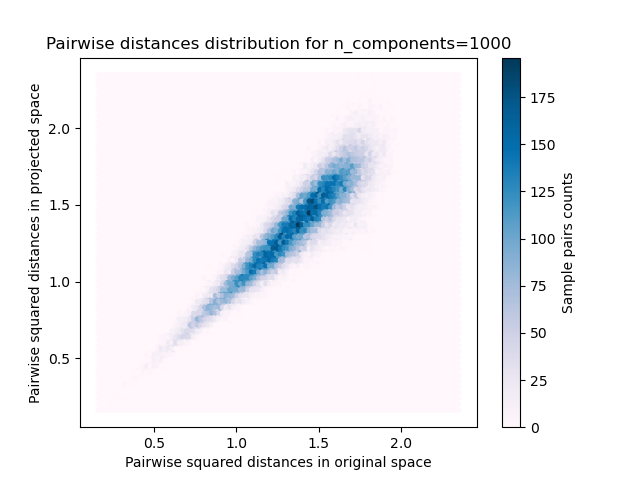
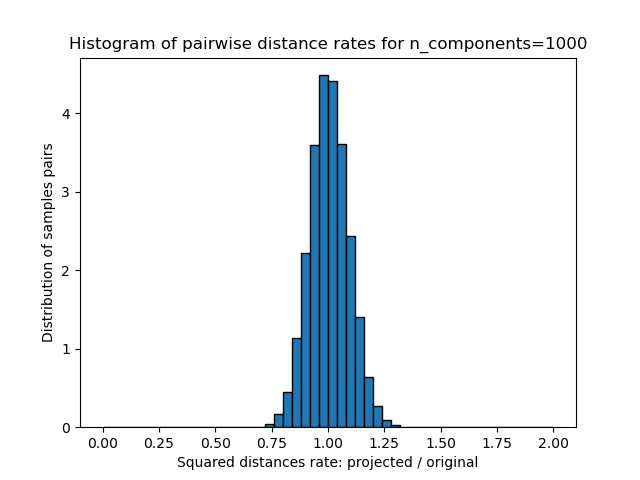
Für jeden Wert von n_components plotten wir

• die 2D-Verteilung von Sample-Paaren mit paarweisen Abständen im ursprünglichen und projizierten Raum als x- bzw. y-Achse.

• das 1D-Histogramm des Verhältnisses dieser Abstände (projiziert / original).

n_samples, n_features = data.shape
print(
    f"Embedding {n_samples} samples with dim {n_features} using various "
    "random projections"
)

n_components_range = np.array([300, 1_000, 10_000])
dists = euclidean_distances(data, squared=True).ravel()

# select only non-identical samples pairs
nonzero = dists != 0
dists = dists[nonzero]

for n_components in n_components_range:
    t0 = time()
    rp = SparseRandomProjection(n_components=n_components)
    projected_data = rp.fit_transform(data)
    print(
        f"Projected {n_samples} samples from {n_features} to {n_components} in "
        f"{time() - t0:0.3f}s"
    )
    if hasattr(rp, "components_"):
        n_bytes = rp.components_.data.nbytes
        n_bytes += rp.components_.indices.nbytes
        print(f"Random matrix with size: {n_bytes / 1e6:0.3f} MB")

    projected_dists = euclidean_distances(projected_data, squared=True).ravel()[nonzero]

    plt.figure()
    min_dist = min(projected_dists.min(), dists.min())
    max_dist = max(projected_dists.max(), dists.max())
    plt.hexbin(
        dists,
        projected_dists,
        gridsize=100,
        cmap=plt.cm.PuBu,
        extent=[min_dist, max_dist, min_dist, max_dist],
    )
    plt.xlabel("Pairwise squared distances in original space")
    plt.ylabel("Pairwise squared distances in projected space")
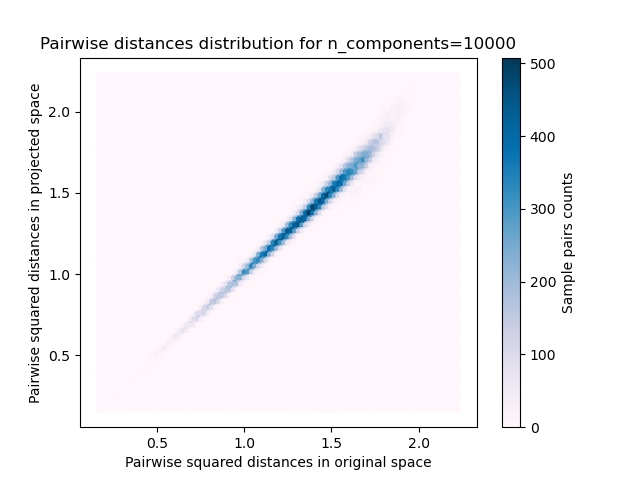
    plt.title("Pairwise distances distribution for n_components=%d" % n_components)
    cb = plt.colorbar()
    cb.set_label("Sample pairs counts")

    rates = projected_dists / dists
    print(f"Mean distances rate: {np.mean(rates):.2f} ({np.std(rates):.2f})")

    plt.figure()
    plt.hist(rates, bins=50, range=(0.0, 2.0), edgecolor="k", density=True)
    plt.xlabel("Squared distances rate: projected / original")
    plt.ylabel("Distribution of samples pairs")
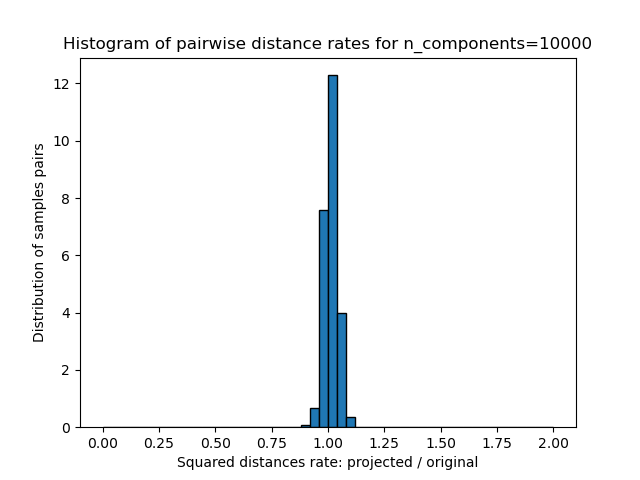
    plt.title("Histogram of pairwise distance rates for n_components=%d" % n_components)

    # TODO: compute the expected value of eps and add them to the previous plot
    # as vertical lines / region

plt.show()

• 
• 
• 
• 
• 
• 

Embedding 300 samples with dim 130107 using various random projections
Projected 300 samples from 130107 to 300 in 0.270s
Random matrix with size: 1.304 MB
Mean distances rate: 1.02 (0.17)
Projected 300 samples from 130107 to 1000 in 0.897s
Random matrix with size: 4.326 MB
Mean distances rate: 1.01 (0.09)
Projected 300 samples from 130107 to 10000 in 8.912s
Random matrix with size: 43.248 MB
Mean distances rate: 1.01 (0.03)

Wir sehen, dass für niedrige Werte von n_components die Verteilung breit ist mit vielen verzerrten Paaren und einer schiefen Verteilung (aufgrund der harten Grenze bei Null auf der linken Seite, da Abstände immer positiv sind), während für größere Werte von n_components die Verzerrung kontrolliert wird und die Abstände durch die Zufallsprojektion gut erhalten bleiben.

Anmerkungen

Laut dem JL-Lemma erfordert die Projektion von 300 Samples ohne zu große Verzerrung mindestens mehrere tausend Dimensionen, unabhängig von der Anzahl der Merkmale des ursprünglichen Datensatzes.

Daher macht die Verwendung von Zufallsprojektionen auf dem digits-Datensatz, der im Eingaberaum nur 64 Merkmale hat, keinen Sinn: Sie ermöglicht in diesem Fall keine Dimensionsreduktion.

Auf der anderen Seite können auf twenty newsgroups die Dimensionen von 56.436 auf 10.000 reduziert werden, während die paarweisen Abstände vernünftig erhalten bleiben.

Verwandte Beispiele

Demo des HDBSCAN Clustering Algorithmus

Demo des HDBSCAN Clustering Algorithmus

Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

Mannigfaltigkeitslernen auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap...

Ledoit-Wolf vs OAS Schätzung

Ledoit-Wolf vs OAS Schätzung

Mehrdimensionale Skalierung

Mehrdimensionale Skalierung