Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Partial Dependence und Individual Conditional Expectation Plots#
Partial-Dependenz-Plots zeigen die Abhängigkeit zwischen der Ziel-Funktion [2] und einer Menge von Merkmalen von Interesse, wobei über die Werte aller anderen Merkmale (der Komplementärmerkmale) marginalisiert wird. Aufgrund der Grenzen der menschlichen Wahrnehmung muss die Größe der Menge der Merkmale von Interesse klein sein (normalerweise eins oder zwei), daher werden sie normalerweise unter den wichtigsten Merkmalen ausgewählt.
Ähnlich zeigt ein Individual Conditional Expectation (ICE) Plot [3] die Abhängigkeit zwischen der Ziel-Funktion und einem Merkmal von Interesse. Im Gegensatz zu Partial-Dependenz-Plots, die den durchschnittlichen Effekt der Merkmale von Interesse zeigen, visualisieren ICE-Plots die Abhängigkeit der Vorhersage von einem Merkmal für jede Stichprobe separat, mit einer Linie pro Stichprobe. Nur ein Merkmal von Interesse wird für ICE-Plots unterstützt.
Dieses Beispiel zeigt, wie Partial-Dependenz- und ICE-Plots von einem MLPRegressor und einem HistGradientBoostingRegressor, trainiert auf dem Bike-Sharing-Datensatz, erhalten werden können. Das Beispiel ist inspiriert von [1].
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Vorverarbeitung des Bike-Sharing-Datensatzes#
Wir verwenden den Bike-Sharing-Datensatz. Das Ziel ist es, die Anzahl der Fahrradausleihen anhand von Wetter-, Saison- und Datums-/Zeitinformationen vorherzusagen.
from sklearn.datasets import fetch_openml
bikes = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
# Make an explicit copy to avoid "SettingWithCopyWarning" from pandas
X, y = bikes.data.copy(), bikes.target
# We use only a subset of the data to speed up the example.
X = X.iloc[::5, :]
y = y[::5]
Das Merkmal "weather" hat eine Besonderheit: die Kategorie "heavy_rain" ist eine seltene Kategorie.
X["weather"].value_counts()
weather
clear 2284
misty 904
rain 287
heavy_rain 1
Name: count, dtype: int64
Aufgrund dieser seltenen Kategorie fassen wir sie zu "rain" zusammen.
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
Wir betrachten nun das Merkmal "year" genauer
X["year"].value_counts()
year
1 1747
0 1729
Name: count, dtype: int64
Wir sehen, dass wir Daten aus zwei Jahren haben. Wir verwenden das erste Jahr zum Trainieren des Modells und das zweite Jahr zum Testen des Modells.
mask_training = X["year"] == 0.0
X = X.drop(columns=["year"])
X_train, y_train = X[mask_training], y[mask_training]
X_test, y_test = X[~mask_training], y[~mask_training]
Wir können die Informationen zum Datensatz überprüfen, um zu sehen, dass wir heterogene Datentypen haben. Wir müssen die verschiedenen Spalten entsprechend vorverarbeiten.
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 1729 entries, 0 to 8640
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 1729 non-null category
1 month 1729 non-null int64
2 hour 1729 non-null int64
3 holiday 1729 non-null category
4 weekday 1729 non-null int64
5 workingday 1729 non-null category
6 weather 1729 non-null category
7 temp 1729 non-null float64
8 feel_temp 1729 non-null float64
9 humidity 1729 non-null float64
10 windspeed 1729 non-null float64
dtypes: category(4), float64(4), int64(3)
memory usage: 115.4 KB
Aus den vorherigen Informationen betrachten wir die category-Spalten als nominale kategoriale Merkmale. Darüber hinaus betrachten wir die Datums- und Zeitinformationen ebenfalls als kategoriale Merkmale.
Wir definieren manuell die Spalten, die numerische und kategoriale Merkmale enthalten.
numerical_features = [
"temp",
"feel_temp",
"humidity",
"windspeed",
]
categorical_features = X_train.columns.drop(numerical_features)
Bevor wir uns den Details zur Vorverarbeitung der verschiedenen Machine-Learning-Pipelines widmen, versuchen wir, zusätzliche Einblicke in den Datensatz zu gewinnen, die hilfreich sind, um die statistische Leistung des Modells und die Ergebnisse der Partial-Dependenz-Analyse zu verstehen.
Wir plotten die durchschnittliche Anzahl der Fahrradausleihen, indem wir die Daten nach Saison und Jahr gruppieren.
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
days = ("Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat")
hours = tuple(range(24))
xticklabels = [f"{day}\n{hour}:00" for day, hour in product(days, hours)]
xtick_start, xtick_period = 6, 12
fig, axs = plt.subplots(nrows=2, figsize=(8, 6), sharey=True, sharex=True)
average_bike_rentals = bikes.frame.groupby(
["year", "season", "weekday", "hour"], observed=True
).mean(numeric_only=True)["count"]
for ax, (idx, df) in zip(axs, average_bike_rentals.groupby("year")):
df.groupby("season", observed=True).plot(ax=ax, legend=True)
# decorate the plot
ax.set_xticks(
np.linspace(
start=xtick_start,
stop=len(xticklabels),
num=len(xticklabels) // xtick_period,
)
)
ax.set_xticklabels(xticklabels[xtick_start::xtick_period])
ax.set_xlabel("")
ax.set_ylabel("Average number of bike rentals")
ax.set_title(
f"Bike rental for {'2010 (train set)' if idx == 0.0 else '2011 (test set)'}"
)
ax.set_ylim(0, 1_000)
ax.set_xlim(0, len(xticklabels))
ax.legend(loc=2)
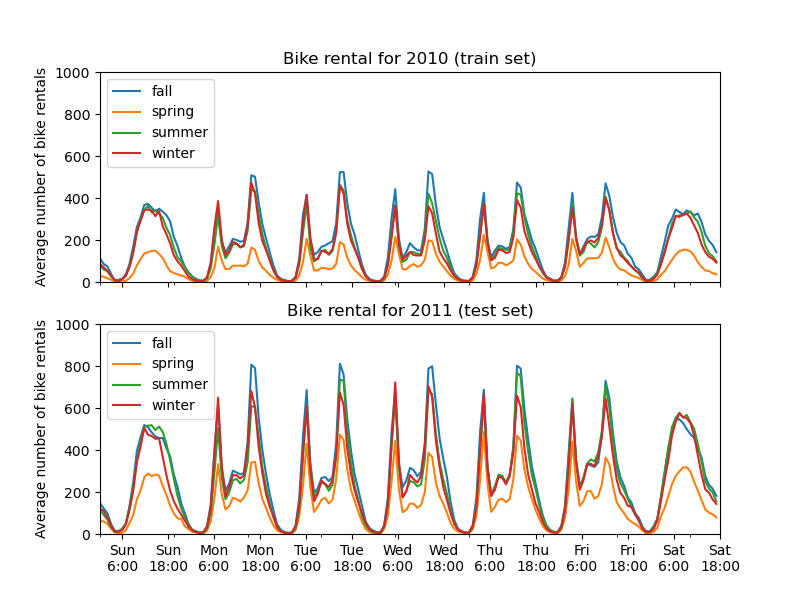
Der erste auffällige Unterschied zwischen dem Trainings- und dem Testset ist, dass die Anzahl der Fahrradausleihen im Testset höher ist. Aus diesem Grund wird es nicht überraschen, wenn ein Machine-Learning-Modell die Anzahl der Fahrradausleihen unterschätzt. Wir beobachten auch, dass die Anzahl der Fahrradausleihen während der Frühlingssaison geringer ist. Außerdem sehen wir, dass während der Werktage ein spezifisches Muster um 6-7 Uhr morgens und 17-18 Uhr abends mit einigen Spitzen bei den Fahrradausleihen auftritt. Wir können diese verschiedenen Erkenntnisse im Hinterkopf behalten und sie zum Verständnis des Partial-Dependenz-Plots verwenden.
Vorverarbeitung für Machine-Learning-Modelle#
Da wir später zwei verschiedene Modelle verwenden werden, einen MLPRegressor und einen HistGradientBoostingRegressor, erstellen wir zwei verschiedene Vorverarbeiter, die für jedes Modell spezifisch sind.
Vorverarbeitung für das neuronale Netzwerkmodell#
Wir verwenden einen QuantileTransformer zur Skalierung der numerischen Merkmale und einen OneHotEncoder zur Kodierung der kategorialen Merkmale.
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, QuantileTransformer
mlp_preprocessor = ColumnTransformer(
transformers=[
("num", QuantileTransformer(n_quantiles=100), numerical_features),
("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features),
]
)
mlp_preprocessor
Vorverarbeitung für das Gradient-Boosting-Modell#
Für das Gradient-Boosting-Modell belassen wir die numerischen Merkmale wie sie sind und kodieren nur die kategorialen Merkmale mit einem OrdinalEncoder.
from sklearn.preprocessing import OrdinalEncoder
hgbdt_preprocessor = ColumnTransformer(
transformers=[
("cat", OrdinalEncoder(), categorical_features),
("num", "passthrough", numerical_features),
],
sparse_threshold=1,
verbose_feature_names_out=False,
).set_output(transform="pandas")
hgbdt_preprocessor
1-Wege-Partial-Dependenz mit verschiedenen Modellen#
In diesem Abschnitt berechnen wir 1-Wege-Partial-Dependenz mit zwei verschiedenen Machine-Learning-Modellen: (i) einem Multi-Layer-Perzeptron und (ii) einem Gradient-Boosting-Modell. Mit diesen beiden Modellen veranschaulichen wir, wie sowohl Partial-Dependenz-Plots (PDP) für numerische und kategoriale Merkmale als auch Individual Conditional Expectation (ICE) berechnet und interpretiert werden.
Multi-Layer-Perzeptron#
Lassen Sie uns einen MLPRegressor anpassen und ein-dimensionale Partial-Dependenz-Plots berechnen.
from time import time
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
print("Training MLPRegressor...")
tic = time()
mlp_model = make_pipeline(
mlp_preprocessor,
MLPRegressor(
hidden_layer_sizes=(30, 15),
learning_rate_init=0.01,
early_stopping=True,
random_state=0,
),
)
mlp_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {mlp_model.score(X_test, y_test):.2f}")
Training MLPRegressor...
done in 0.563s
Test R2 score: 0.61
Wir haben eine Pipeline mit dem speziell für das neuronale Netzwerk erstellten Vorverarbeiter konfiguriert und die Größe des neuronalen Netzwerks sowie die Lernrate abgestimmt, um einen angemessenen Kompromiss zwischen Trainingszeit und Vorhersageleistung auf einem Testdatensatz zu erzielen.
Wichtig ist, dass dieser tabellarische Datensatz sehr unterschiedliche dynamische Bereiche für seine Merkmale aufweist. Neuronale Netzwerke sind tendenziell sehr empfindlich gegenüber Merkmalen mit unterschiedlichen Skalen, und das Vergessen der Vorverarbeitung des numerischen Merkmals würde zu einem sehr schlechten Modell führen.
Es wäre möglich, mit einem größeren neuronalen Netzwerk eine noch höhere Vorhersageleistung zu erzielen, aber das Training wäre auch erheblich teurer.
Beachten Sie, dass es wichtig ist zu überprüfen, ob das Modell auf einem Testdatensatz genau genug ist, bevor der Partial-Dependenz-Plot erstellt wird, da es wenig Sinn hätte, die Auswirkung eines bestimmten Merkmals auf die Vorhersagefunktion eines Modells mit schlechter Vorhersageleistung zu erklären. In dieser Hinsicht funktioniert unser MLP-Modell recht gut.
Wir werden die gemittelte Partial-Dependenz plotten.
import matplotlib.pyplot as plt
from sklearn.inspection import PartialDependenceDisplay
common_params = {
"subsample": 50,
"n_jobs": 2,
"grid_resolution": 20,
"random_state": 0,
}
print("Computing partial dependence plots...")
features_info = {
# features of interest
"features": ["temp", "humidity", "windspeed", "season", "weather", "hour"],
# type of partial dependence plot
"kind": "average",
# information regarding categorical features
"categorical_features": categorical_features,
}
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
mlp_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
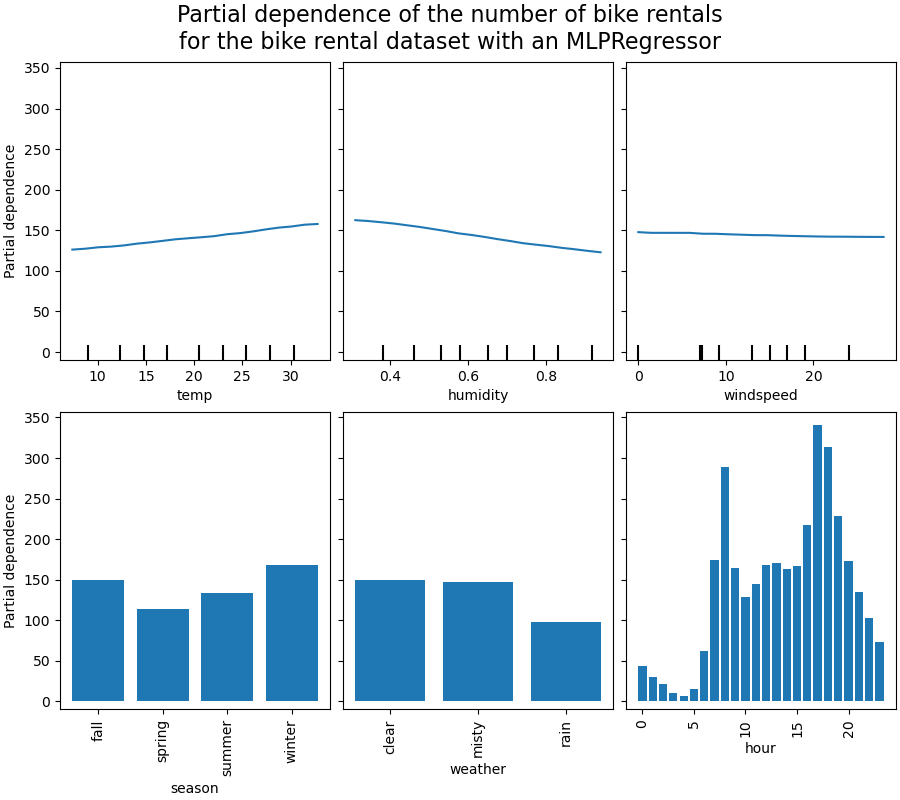
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with an MLPRegressor"
),
fontsize=16,
)
Computing partial dependence plots...
done in 0.468s
Gradient Boosting#
Lassen Sie uns nun einen HistGradientBoostingRegressor anpassen und die Partial-Dependenz für dieselben Merkmale berechnen. Wir verwenden auch den spezifischen Vorverarbeiter, den wir für dieses Modell erstellt haben.
from sklearn.ensemble import HistGradientBoostingRegressor
print("Training HistGradientBoostingRegressor...")
tic = time()
hgbdt_model = make_pipeline(
hgbdt_preprocessor,
HistGradientBoostingRegressor(
categorical_features=categorical_features,
random_state=0,
max_iter=50,
),
)
hgbdt_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {hgbdt_model.score(X_test, y_test):.2f}")
Training HistGradientBoostingRegressor...
done in 0.111s
Test R2 score: 0.62
Hier haben wir die Standardhyperparameter für das Gradient-Boosting-Modell ohne Vorverarbeitung verwendet, da baumbasierte Modelle von monotonen Transformationen numerischer Merkmale natürlich robust sind.
Beachten Sie, dass auf diesem tabellarischen Datensatz Gradient Boosting Machines sowohl signifikant schneller zu trainieren als auch genauer als neuronale Netzwerke sind. Außerdem ist es signifikant kostengünstiger, ihre Hyperparameter abzustimmen (die Standardwerte funktionieren tendenziell gut, was bei neuronalen Netzwerken oft nicht der Fall ist).
Wir werden die Partial-Dependenz für einige der numerischen und kategorialen Merkmale plotten.
print("Computing partial dependence plots...")
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
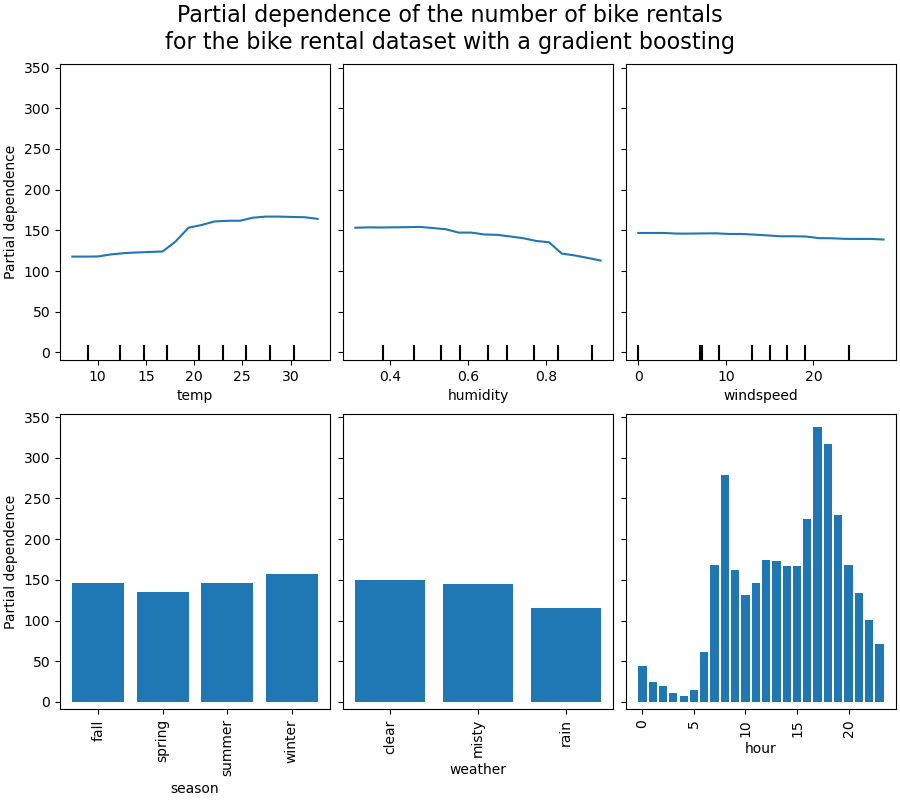
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with a gradient boosting"
),
fontsize=16,
)
Computing partial dependence plots...
done in 0.948s
Analyse der Plots#
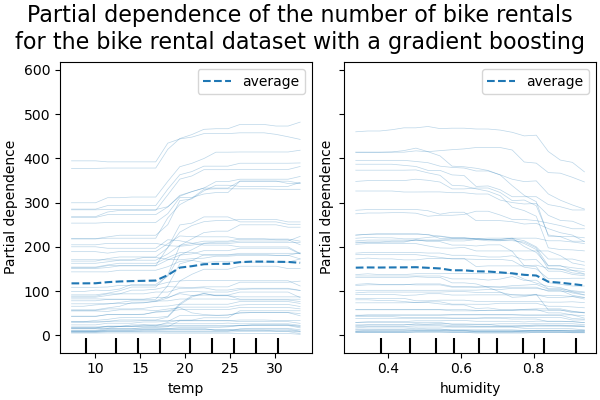
Wir betrachten zunächst die PDPs für die numerischen Merkmale. Für beide Modelle zeigt der allgemeine Trend der PDP der Temperatur, dass die Anzahl der Fahrradausleihen mit der Temperatur zunimmt. Wir können eine ähnliche Analyse mit entgegengesetztem Trend für die Luftfeuchtigkeitsmerkmale durchführen. Die Anzahl der Fahrradausleihen nimmt mit zunehmender Luftfeuchtigkeit ab. Schließlich sehen wir denselben Trend für das Merkmal Windgeschwindigkeit. Die Anzahl der Fahrradausleihen nimmt mit zunehmender Windgeschwindigkeit für beide Modelle ab. Wir beobachten auch, dass der MLPRegressor viel glattere Vorhersagen hat als der HistGradientBoostingRegressor.
Nun betrachten wir die Partial-Dependenz-Plots für die kategorialen Merkmale.
Wir beobachten, dass die Frühlingssaison die niedrigste Balken für das Merkmal Saison ist. Beim Merkmal Wetter ist die Kategorie Regen der niedrigste Balken. Bezüglich der Stunde sehen wir zwei Spitzen um 7 Uhr morgens und 18 Uhr abends. Diese Ergebnisse stehen im Einklang mit den früheren Beobachtungen zum Datensatz.
Es ist jedoch erwähnenswert, dass wir potenziell bedeutunglose synthetische Stichproben erstellen, wenn Merkmale korreliert sind.
ICE vs. PDP#
PDP ist ein Durchschnitt der marginalen Effekte der Merkmale. Wir mitteln die Antwort aller Stichproben der bereitgestellten Menge. Daher könnten einige Effekte verborgen bleiben. In diesem Sinne ist es möglich, jede einzelne Antwort zu plotten. Diese Darstellung wird als Individual Effect Plot (ICE) bezeichnet. Im folgenden Plot zeigen wir 50 zufällig ausgewählte ICEs für die Merkmale Temperatur und Luftfeuchtigkeit.
print("Computing partial dependence plots and individual conditional expectation...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
"centered": True,
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
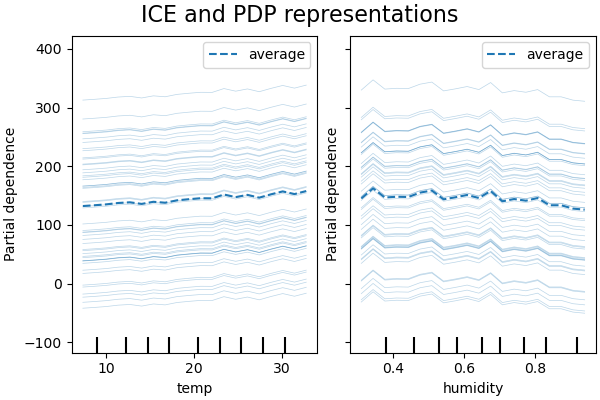
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)

Computing partial dependence plots and individual conditional expectation...
done in 0.394s
Wir sehen, dass der ICE für das Merkmal Temperatur zusätzliche Informationen liefert: Einige der ICE-Linien sind flach, während andere einen Rückgang der Abhängigkeit für Temperaturen über 35 Grad Celsius zeigen. Wir beobachten ein ähnliches Muster für das Merkmal Luftfeuchtigkeit: Einige der ICE-Linien zeigen einen starken Rückgang, wenn die Luftfeuchtigkeit über 80 % liegt.
Nicht alle ICE-Linien sind parallel, was darauf hindeutet, dass das Modell Interaktionen zwischen den Merkmalen findet. Wir können das Experiment wiederholen, indem wir das Gradient-Boosting-Modell so einschränken, dass es keine Interaktionen zwischen den Merkmalen verwendet, indem wir den Parameter interaction_cst verwenden.
from sklearn.base import clone
interaction_cst = [[i] for i in range(X_train.shape[1])]
hgbdt_model_without_interactions = (
clone(hgbdt_model)
.set_params(histgradientboostingregressor__interaction_cst=interaction_cst)
.fit(X_train, y_train)
)
print(f"Test R2 score: {hgbdt_model_without_interactions.score(X_test, y_test):.2f}")
Test R2 score: 0.38
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info["centered"] = False
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)
2D-Interaktionsplots#
PDPs mit zwei Merkmalen von Interesse ermöglichen es uns, Interaktionen zwischen ihnen zu visualisieren. ICEs können jedoch nicht auf einfache Weise geplottet und somit interpretiert werden. Wir zeigen die in from_estimator verfügbare Darstellung, ein 2D-Heatmap.
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)

Computing partial dependence plots...
done in 6.743s
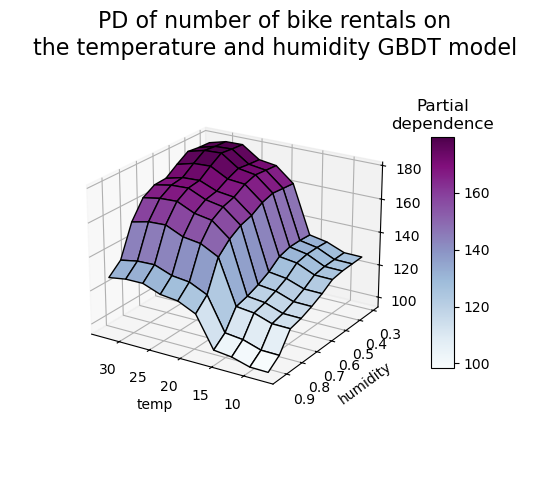
Der Zwei-Wege-Partial-Dependenz-Plot zeigt die Abhängigkeit der Anzahl der Fahrradausleihen von gemeinsamen Werten für Temperatur und Luftfeuchtigkeit. Wir sehen deutlich eine Interaktion zwischen den beiden Merkmalen. Bei einer Temperatur über 20 Grad Celsius scheint die Luftfeuchtigkeit die Anzahl der Fahrradausleihen zu beeinflussen, was unabhängig von der Temperatur zu sein scheint.
Andererseits beeinflussen bei Temperaturen unter 20 Grad Celsius sowohl die Temperatur als auch die Luftfeuchtigkeit kontinuierlich die Anzahl der Fahrradausleihen.
Darüber hinaus hängt die Steigung des Einflusses des 20-Grad-Celsius-Schwellenwerts stark von der Luftfeuchtigkeit ab: Die Steigung ist unter trockenen Bedingungen stark, unter feuchteren Bedingungen über 70 % Luftfeuchtigkeit jedoch viel sanfter.
Wir kontrastieren diese Ergebnisse nun mit denselben Plots, die für das Modell berechnet wurden, das darauf beschränkt ist, eine Vorhersagefunktion zu lernen, die nicht von solchen nicht-linearen Merkmalsinteraktionen abhängt.
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)

Computing partial dependence plots...
done in 6.157s
Die 1D-Partial-Dependenz-Plots für das Modell, das darauf beschränkt ist, keine Merkmalsinteraktionen zu modellieren, zeigen lokale Spitzen für jedes Merkmal einzeln, insbesondere für das Merkmal "Luftfeuchtigkeit". Diese Spitzen spiegeln möglicherweise ein verschlechtertes Verhalten des Modells wider, das versucht, die verbotenen Interaktionen irgendwie zu kompensieren, indem es bestimmte Trainingspunkte übermäßig anpasst. Beachten Sie, dass die Vorhersageleistung dieses Modells, gemessen auf dem Testdatensatz, signifikant schlechter ist als die des ursprünglichen, unbeschränkten Modells.
Beachten Sie auch, dass die Anzahl der sichtbaren lokalen Spitzen in diesen Plots von der Gitterauflösungsparameter des PD-Plots selbst abhängt.
Diese lokalen Spitzen führen zu einem verrauschten 2D-PD-Plot. Es ist ziemlich schwierig zu sagen, ob zwischen diesen Merkmalen keine Interaktion besteht, da die hochfrequenten Oszillationen im Merkmal Luftfeuchtigkeit vorhanden sind. Es ist jedoch deutlich zu sehen, dass der einfache Interaktionseffekt, der beobachtet wird, wenn die Temperatur die 20-Grad-Grenze überschreitet, für dieses Modell nicht mehr sichtbar ist.
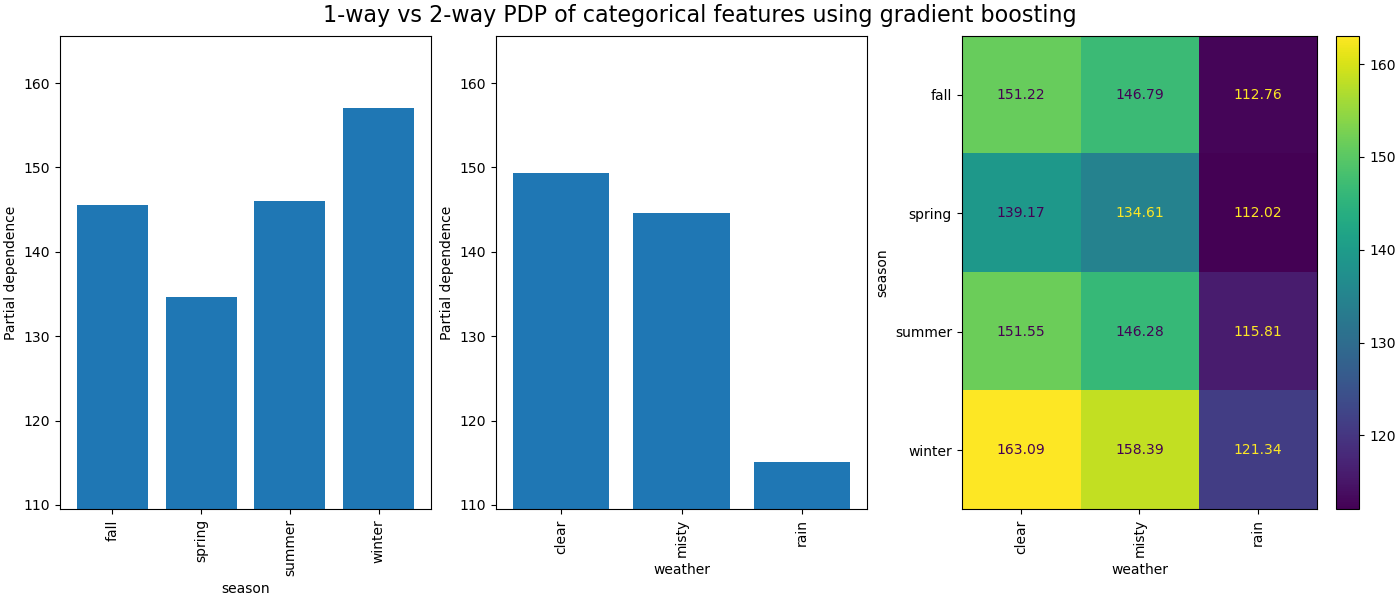
Die partielle Abhängigkeit zwischen kategorialen Merkmalen liefert eine diskrete Darstellung, die als Heatmap dargestellt werden kann. Zum Beispiel wäre die Interaktion zwischen der Saison, dem Wetter und dem Ziel wie folgt
print("Computing partial dependence plots...")
features_info = {
"features": ["season", "weather", ("season", "weather")],
"kind": "average",
"categorical_features": categorical_features,
}
_, ax = plt.subplots(ncols=3, figsize=(14, 6), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way PDP of categorical features using gradient boosting", fontsize=16
)
Computing partial dependence plots...
done in 0.331s
3D-Darstellung#
Machen wir denselben Partial-Dependenz-Plot für die 2-Merkmals-Interaktion, diesmal in 3 Dimensionen.
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
import numpy as np
from sklearn.inspection import partial_dependence
fig = plt.figure(figsize=(5.5, 5))
features = ("temp", "humidity")
pdp = partial_dependence(
hgbdt_model, X_train, features=features, kind="average", grid_resolution=10
)
XX, YY = np.meshgrid(pdp["grid_values"][0], pdp["grid_values"][1])
Z = pdp.average[0].T
ax = fig.add_subplot(projection="3d")
fig.add_axes(ax)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1, cmap=plt.cm.BuPu, edgecolor="k")
ax.set_xlabel(features[0])
ax.set_ylabel(features[1])
fig.suptitle(
"PD of number of bike rentals on\nthe temperature and humidity GBDT model",
fontsize=16,
)
# pretty init view
ax.view_init(elev=22, azim=122)
clb = plt.colorbar(surf, pad=0.08, shrink=0.6, aspect=10)
clb.ax.set_title("Partial\ndependence")
plt.show()
Benutzerdefinierte Inspektionpunkte#
In keinem der bisherigen Beispiele wird spezifiziert, _welche_ Punkte zur Erstellung der Partial-Dependenz-Plots ausgewertet werden. Standardmäßig verwenden wir Perzentile, die durch den Eingabedatensatz definiert sind. In einigen Fällen kann es hilfreich sein, die genauen Punkte anzugeben, an denen das Modell ausgewertet werden soll. Beispielsweise wenn ein Benutzer das Modellverhalten bei Out-of-Distribution-Daten testen oder zwei Modelle vergleichen möchte, die auf leicht unterschiedlichen Daten angepasst wurden. Der Parameter custom_values ermöglicht es dem Benutzer, die Werte anzugeben, auf denen das Modell ausgewertet werden soll. Dies überschreibt die Parameter grid_resolution und percentiles. Kehren wir zu unserem obigen Gradient-Boosting-Beispiel zurück, aber mit benutzerdefinierten Werten.
print("Computing partial dependence plots with custom evaluation values...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
# we set custom values for temp feature -
# all other features are evaluated based on the data
custom_values={"temp": np.linspace(0, 40, 10)},
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with a gradient boosting"
),
fontsize=16,
)
Computing partial dependence plots with custom evaluation values...
done in 0.403s
Gesamtlaufzeit des Skripts: (0 Minuten 20,237 Sekunden)
Verwandte Beispiele