Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Ridge-Koeffizienten als Funktion der L2-Regularisierung#
Ein Modell, das überangepasst ist, lernt die Trainingsdaten zu gut und erfasst sowohl die zugrunde liegenden Muster als auch das Rauschen in den Daten. Wenn es jedoch auf ungesehene Daten angewendet wird, gelten die gelernten Assoziationen möglicherweise nicht. Dies erkennen wir normalerweise, wenn wir unsere trainierten Vorhersagen auf die Testdaten anwenden und einen signifikanten Rückgang der statistischen Leistung im Vergleich zu den Trainingsdaten feststellen.
Eine Möglichkeit, Überanpassung zu überwinden, ist die Regularisierung, die durch Bestrafung großer Gewichte (Koeffizienten) in linearen Modellen erreicht werden kann, wodurch das Modell gezwungen wird, alle Koeffizienten zu schrumpfen. Regularisierung reduziert die Abhängigkeit eines Modells von spezifischen Informationen, die aus den Trainingsstichproben gewonnen wurden.
Dieses Beispiel veranschaulicht, wie die L2-Regularisierung in einer Ridge-Regression die Leistung eines Modells beeinflusst, indem ein Strafterm zur Verlustfunktion hinzugefügt wird, der mit den Koeffizienten \(\beta\) zunimmt.
Die regularisierte Verlustfunktion ist gegeben durch: \(\mathcal{L}(X, y, \beta) = \| y - X \beta \|^{2}_{2} + \alpha \| \beta \|^{2}_{2}\)
wobei \(X\) die Eingabedaten sind, \(y\) die Zielvariable ist, \(\beta\) der Vektor der mit den Merkmalen verbundenen Koeffizienten ist und \(\alpha\) die Regularisierungsstärke ist.
Die regularisierte Verlustfunktion zielt darauf ab, den Kompromiss zwischen der genauen Vorhersage des Trainingsdatensatzes und der Vermeidung von Überanpassung auszugleichen.
Bei diesem regularisierten Verlust misst die linke Seite (z. B. \(\|y - X\beta\|^{2}_{2}\)) die quadratische Differenz zwischen der tatsächlichen Zielvariablen \(y\) und den vorhergesagten Werten. Die Minimierung dieses Terms allein könnte zu Überanpassung führen, da das Modell zu komplex und empfindlich auf Rauschen in den Trainingsdaten reagieren könnte.
Um Überanpassung zu begegnen, fügt die Ridge-Regularisierung eine Beschränkung, den sogenannten Strafterm (\(\alpha \| \beta\|^{2}_{2}\)), zur Verlustfunktion hinzu. Dieser Strafterm ist die Summe der Quadrate der Koeffizienten des Modells, multipliziert mit der Regularisierungsstärke \(\alpha\). Durch die Einführung dieser Beschränkung entmutigt die Ridge-Regularisierung jeden einzelnen Koeffizienten \(\beta_{i}\), einen übermäßig großen Wert anzunehmen, und fördert kleinere und gleichmäßigere Koeffizienten. Höhere Werte von \(\alpha\) zwingen die Koeffizienten gegen Null. Ein übermäßig hohes \(\alpha\) kann jedoch zu einem unterangepassten Modell führen, das wichtige Muster in den Daten nicht erfasst.
Daher kombiniert die regularisierte Verlustfunktion den Term der Vorhersagegenauigkeit und den Strafterm. Durch Anpassung der Regularisierungsstärke können Praktiker den Grad der Beschränkung, der auf die Gewichte angewendet wird, feinabstimmen und ein Modell trainieren, das gut auf ungesehene Daten generalisiert und gleichzeitig Überanpassung vermeidet.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Zweck dieses Beispiels#
Um zu zeigen, wie die Ridge-Regularisierung funktioniert, erstellen wir einen Datensatz ohne Rauschen. Dann trainieren wir ein regularisiertes Modell mit einer Reihe von Regularisierungsstärken (\(\alpha\)) und zeichnen auf, wie sich die trainierten Koeffizienten und der mittlere quadratische Fehler zwischen diesen und den ursprünglichen Werten als Funktion der Regularisierungsstärke verhalten.
Erstellung eines Datensatzes ohne Rauschen#
Wir erstellen einen Spiel-Datensatz mit 100 Stichproben und 10 Merkmalen, der für die Erkennung von Regressionen geeignet ist. Von den 10 Merkmalen sind 8 informativ und tragen zur Regression bei, während die verbleibenden 2 Merkmale keinen Einfluss auf die Zielvariable haben (ihre wahren Koeffizienten sind 0). Bitte beachten Sie, dass in diesem Beispiel die Daten rauschfrei sind, daher können wir davon ausgehen, dass unser Regressionsmodell die wahren Koeffizienten w exakt wiederherstellt.
from sklearn.datasets import make_regression
X, y, w = make_regression(
n_samples=100, n_features=10, n_informative=8, coef=True, random_state=1
)
# Obtain the true coefficients
print(f"The true coefficient of this regression problem are:\n{w}")
The true coefficient of this regression problem are:
[38.32634568 88.49665188 0. 29.75747153 0. 19.08699432
25.44381023 38.69892343 49.28808734 71.75949622]
Training des Ridge-Regressors#
Wir verwenden Ridge, ein lineares Modell mit L2-Regularisierung. Wir trainieren mehrere Modelle, jedes mit einem anderen Wert für den Modellparameter alpha, der eine positive Konstante ist, die den Strafterm multipliziert und die Regularisierungsstärke steuert. Für jedes trainierte Modell berechnen wir dann den Fehler zwischen den wahren Koeffizienten w und den vom Modell gefundenen Koeffizienten clf. Wir speichern die identifizierten Koeffizienten und die berechneten Fehler für die entsprechenden Koeffizienten in Listen, was uns die Darstellung erleichtert.
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
clf = Ridge()
# Generate values for `alpha` that are evenly distributed on a logarithmic scale
alphas = np.logspace(-3, 4, 200)
coefs = []
errors_coefs = []
# Train the model with different regularisation strengths
for a in alphas:
clf.set_params(alpha=a).fit(X, y)
coefs.append(clf.coef_)
errors_coefs.append(mean_squared_error(clf.coef_, w))
Darstellung trainierter Koeffizienten und mittlerer quadratischer Fehler#
Wir stellen nun die 10 verschiedenen regularisierten Koeffizienten als Funktion des Regularisierungsparameters alpha dar, wobei jede Farbe einen anderen Koeffizienten repräsentiert.
Auf der rechten Seite stellen wir dar, wie sich die Fehler der Koeffizienten vom Schätzer als Funktion der Regularisierung ändern.
import matplotlib.pyplot as plt
import pandas as pd
alphas = pd.Index(alphas, name="alpha")
coefs = pd.DataFrame(coefs, index=alphas, columns=[f"Feature {i}" for i in range(10)])
errors = pd.Series(errors_coefs, index=alphas, name="Mean squared error")
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
coefs.plot(
ax=axs[0],
logx=True,
title="Ridge coefficients as a function of the regularization strength",
)
axs[0].set_ylabel("Ridge coefficient values")
errors.plot(
ax=axs[1],
logx=True,
title="Coefficient error as a function of the regularization strength",
)
_ = axs[1].set_ylabel("Mean squared error")
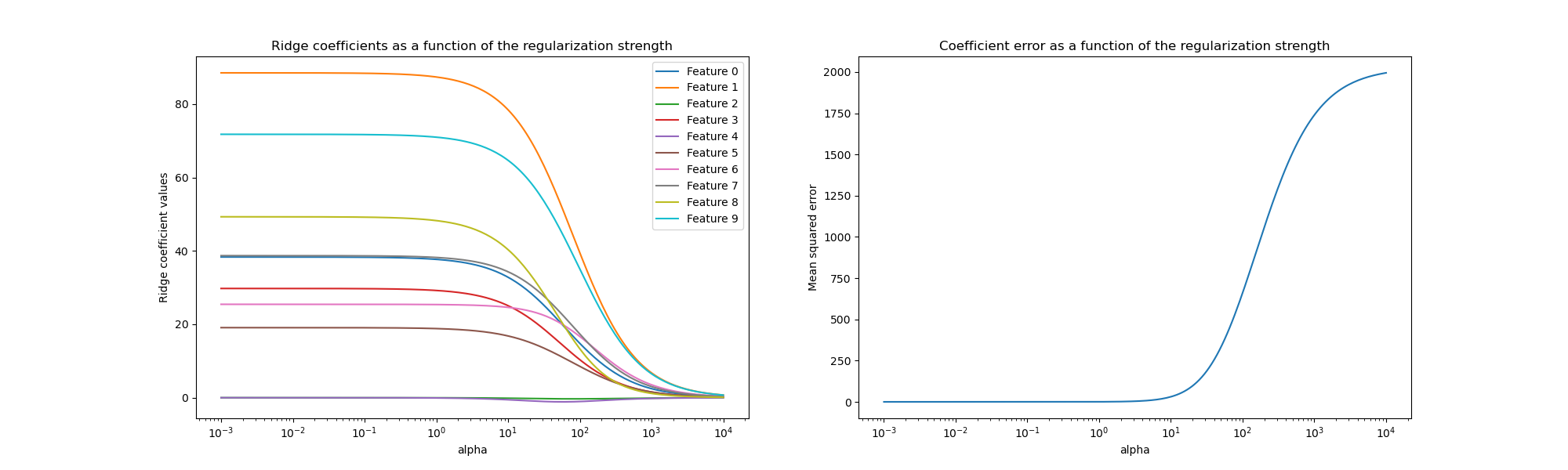
Interpretation der Diagramme#
Das Diagramm auf der linken Seite zeigt, wie die Regularisierungsstärke (alpha) die Ridge-Regressionskoeffizienten beeinflusst. Kleinere Werte von alpha (schwache Regularisierung) lassen die Koeffizienten den wahren Koeffizienten (w) ähneln, die zur Erzeugung des Datensatzes verwendet wurden. Das liegt daran, dass unserem künstlichen Datensatz kein zusätzliches Rauschen hinzugefügt wurde. Wenn alpha steigt, schrumpfen die Koeffizienten gegen Null, wodurch der Einfluss der zuvor wichtigeren Merkmale allmählich reduziert wird.
Die rechte Diagrammhälfte zeigt den mittleren quadratischen Fehler (MSE) zwischen den vom Modell gefundenen Koeffizienten und den wahren Koeffizienten (w). Sie liefert ein Maß dafür, wie genau unser Ridge-Modell im Vergleich zum wahren generativen Modell ist. Ein geringer Fehler bedeutet, dass es Koeffizienten gefunden hat, die näher an denen des wahren generativen Modells liegen. In diesem Fall, da unser Spiel-Datensatz rauschfrei war, können wir sehen, dass das am wenigsten regularisierte Modell Koeffizienten findet, die den wahren Koeffizienten (w) am nächsten kommen (Fehler nahe 0).
Wenn alpha klein ist, erfasst das Modell die komplexen Details der Trainingsdaten, unabhängig davon, ob diese durch Rauschen oder tatsächliche Informationen verursacht wurden. Wenn alpha steigt, schrumpfen die höchsten Koeffizienten schneller, wodurch ihre entsprechenden Merkmale im Trainingsprozess weniger Einfluss haben. Dies kann die Fähigkeit eines Modells zur Generalisierung auf ungesehene Daten verbessern (wenn viel Rauschen erfasst werden musste), birgt aber auch das Risiko eines Leistungsverlusts, wenn die Regularisierung im Vergleich zur Datenmenge zu stark wird (wie in diesem Beispiel).
In realen Szenarien, in denen Daten typischerweise Rauschen enthalten, ist die Auswahl eines geeigneten alpha-Wertes entscheidend, um ein Gleichgewicht zwischen einem über- und einem unterangepassten Modell zu finden.
Hier haben wir gesehen, dass Ridge einen Strafterm zu den Koeffizienten hinzufügt, um Überanpassung zu bekämpfen. Ein weiteres Problem hängt mit dem Vorhandensein von Ausreißern im Trainingsdatensatz zusammen. Ein Ausreißer ist ein Datenpunkt, der sich signifikant von anderen Beobachtungen unterscheidet. Konkret wirken sich diese Ausreißer auf den linken Term der Verlustfunktion aus, den wir zuvor gezeigt haben. Einige andere lineare Modelle sind so formuliert, dass sie robust gegenüber Ausreißern sind, wie z. B. der HuberRegressor. Sie können mehr darüber im Beispiel HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern erfahren.
Gesamtlaufzeit des Skripts: (0 Minuten 0.571 Sekunden)
Verwandte Beispiele
Ridge-Koeffizienten als Funktion der Regularisierung plotten
Auswirkung der Modellregularisierung auf Trainings- und Testfehler
Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle
Regularisierungspfad der L1-Logistischen Regression