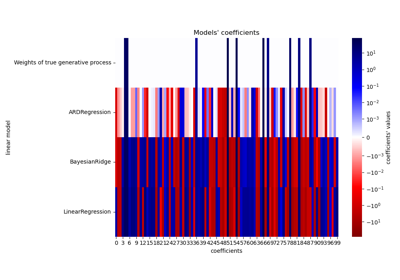
Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Polynomial- und Spline-Interpolation#
Dieses Beispiel demonstriert, wie eine Funktion mit Polynomen bis zum Grad degree mithilfe von Ridge-Regression approximiert werden kann. Wir zeigen zwei verschiedene Möglichkeiten, gegeben n_samples 1D-Punkte x_i
PolynomialFeaturesgeneriert alle Monome bis zum Graddegree. Dies ergibt die sogenannte Vandermonde-Matrix mitn_samplesZeilen unddegree + 1Spalten[[1, x_0, x_0 ** 2, x_0 ** 3, ..., x_0 ** degree], [1, x_1, x_1 ** 2, x_1 ** 3, ..., x_1 ** degree], ...]
Intuitiv kann diese Matrix als eine Matrix von Pseudofunktionen (die Punkte zu einer bestimmten Potenz erhoben) interpretiert werden. Die Matrix ähnelt (aber ist nicht identisch mit) der Matrix, die durch einen Polynomkern induziert wird.
SplineTransformergeneriert B-Spline-Basisfunktionen. Eine Basisfunktion eines B-Splines ist eine stückweise Polynomfunktion vom Graddegree, die nur zwischendegree+1aufeinanderfolgenden Knoten nicht null ist. Bei einer Anzahl vonn_knotsKnoten ergibt dies eine Matrix mitn_samplesZeilen undn_knots + degree - 1Spalten[[basis_1(x_0), basis_2(x_0), ...], [basis_1(x_1), basis_2(x_1), ...], ...]
Dieses Beispiel zeigt, dass diese beiden Transformer gut geeignet sind, nichtlineare Effekte mit einem linearen Modell zu modellieren, indem eine Pipeline verwendet wird, um nichtlineare Merkmale hinzuzufügen. Kernel-Methoden erweitern diese Idee und können sehr hochdimensionale (sogar unendliche) Merkmalsräume induzieren.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer
Wir beginnen mit der Definition einer Funktion, die wir approximieren wollen, und bereiten sie für die Darstellung vor.
def f(x):
"""Function to be approximated by polynomial interpolation."""
return x * np.sin(x)
# whole range we want to plot
x_plot = np.linspace(-1, 11, 100)
Um es interessant zu gestalten, geben wir nur eine kleine Teilmenge von Punkten zum Trainieren an.
x_train = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
x_train = np.sort(rng.choice(x_train, size=20, replace=False))
y_train = f(x_train)
# create 2D-array versions of these arrays to feed to transformers
X_train = x_train[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]
Nun sind wir bereit, Polynommerkmale und Splines zu erstellen, auf den Trainingspunkten zu fitten und zu zeigen, wie gut sie interpolieren.
# plot function
lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(
color=["black", "teal", "yellowgreen", "gold", "darkorange", "tomato"]
)
ax.plot(x_plot, f(x_plot), linewidth=lw, label="ground truth")
# plot training points
ax.scatter(x_train, y_train, label="training points")
# polynomial features
for degree in [3, 4, 5]:
model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=1e-3))
model.fit(X_train, y_train)
y_plot = model.predict(X_plot)
ax.plot(x_plot, y_plot, label=f"degree {degree}")
# B-spline with 4 + 3 - 1 = 6 basis functions
model = make_pipeline(SplineTransformer(n_knots=4, degree=3), Ridge(alpha=1e-3))
model.fit(X_train, y_train)
y_plot = model.predict(X_plot)
ax.plot(x_plot, y_plot, label="B-spline")
ax.legend(loc="lower center")
ax.set_ylim(-20, 10)
plt.show()

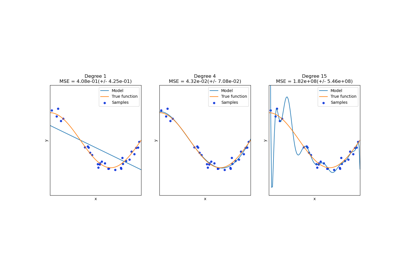
Dies zeigt gut, dass Polynome höheren Grades die Daten besser anpassen können. Gleichzeitig können zu hohe Potenzen unerwünschte Oszillationen zeigen und sind besonders gefährlich für die Extrapolation über den Bereich der gefitteten Daten hinaus. Dies ist ein Vorteil von B-Splines. Sie passen die Daten normalerweise genauso gut an wie Polynome und zeigen ein sehr schönes und glattes Verhalten. Sie haben auch gute Optionen zur Steuerung der Extrapolation, die standardmäßig eine Fortsetzung mit einer Konstanten aufweisen. Beachten Sie, dass Sie meistens eher die Anzahl der Knoten erhöhen, aber degree=3 beibehalten würden.
Um weitere Einblicke in die generierten Merkmalsbasen zu geben, plotten wir separat alle Spalten beider Transformer.
fig, axes = plt.subplots(ncols=2, figsize=(16, 5))
pft = PolynomialFeatures(degree=3).fit(X_train)
axes[0].plot(x_plot, pft.transform(X_plot))
axes[0].legend(axes[0].lines, [f"degree {n}" for n in range(4)])
axes[0].set_title("PolynomialFeatures")
splt = SplineTransformer(n_knots=4, degree=3).fit(X_train)
axes[1].plot(x_plot, splt.transform(X_plot))
axes[1].legend(axes[1].lines, [f"spline {n}" for n in range(6)])
axes[1].set_title("SplineTransformer")
# plot knots of spline
knots = splt.bsplines_[0].t
axes[1].vlines(knots[3:-3], ymin=0, ymax=0.8, linestyles="dashed")
plt.show()
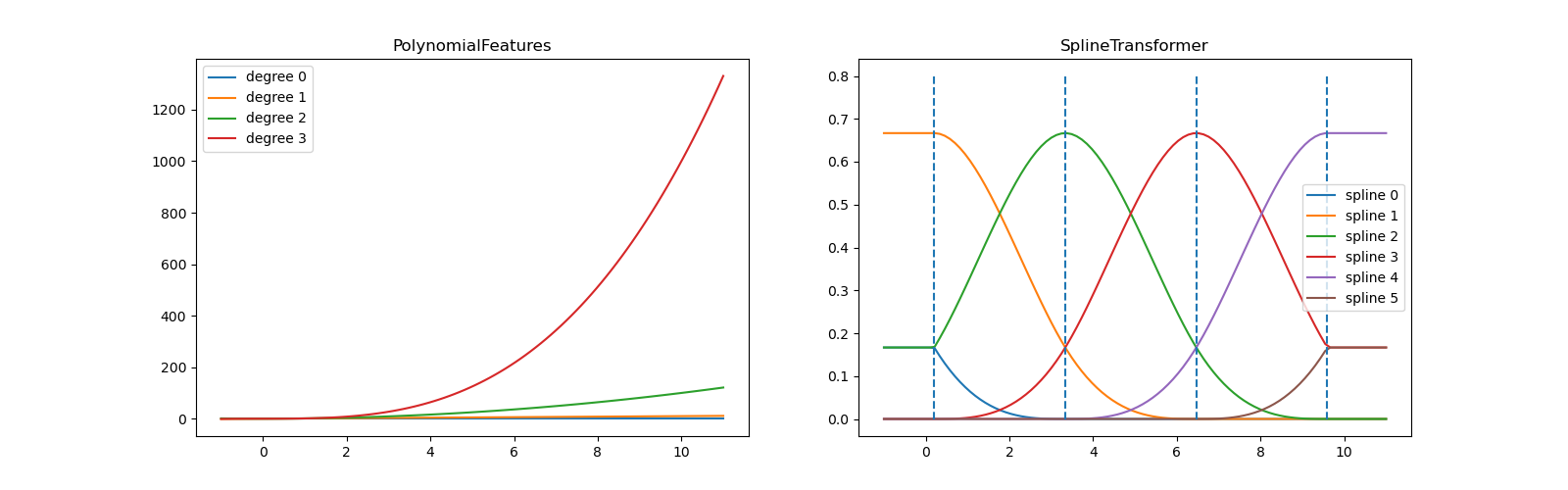
Im linken Plot erkennen wir die Linien, die einfachen Monomen von x**0 bis x**3 entsprechen. Im rechten Diagramm sehen wir die sechs B-Spline-Basisfunktionen vom Grad degree=3 und auch die vier Knotenpositionen, die während fit gewählt wurden. Beachten Sie, dass es degree zusätzliche Knoten links und rechts vom gefitteten Intervall gibt. Diese sind aus technischen Gründen vorhanden, daher verzichten wir darauf, sie zu zeigen. Jede Basisfunktion hat eine lokale Unterstützung und wird über den gefitteten Bereich hinaus als Konstante fortgesetzt. Dieses Extrapolationsverhalten könnte durch das Argument extrapolation geändert werden.
Periodische Splines#
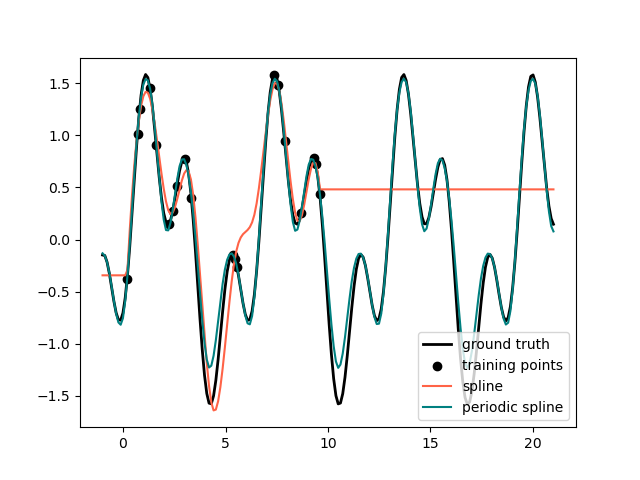
Im vorherigen Beispiel haben wir die Einschränkungen von Polynomen und Splines für die Extrapolation über den Bereich der Trainingsbeobachtungen hinaus gesehen. In einigen Fällen, z. B. bei saisonalen Effekten, erwarten wir eine periodische Fortsetzung des zugrunde liegenden Signals. Solche Effekte können mit periodischen Splines modelliert werden, die die gleiche Funktionswerte und Ableitungen an den ersten und letzten Knoten haben. Im folgenden Fall zeigen wir, wie periodische Splines sowohl innerhalb als auch außerhalb des Bereichs der Trainingsdaten eine bessere Anpassung bieten, wenn die zusätzliche Information der Periodizität gegeben ist. Die Periode der Splines ist der Abstand zwischen dem ersten und letzten Knoten, den wir manuell angeben.
Periodische Splines können auch für natürlich periodische Merkmale (wie den Tag des Jahres) nützlich sein, da die Glattheit an den Grenzpunkten einen Sprung in den transformierten Werten verhindert (z. B. vom 31. Dezember zum 1. Januar). Für solche natürlich periodischen Merkmale oder allgemeiner für Merkmale, bei denen die Periode bekannt ist, wird empfohlen, diese Information explizit an den SplineTransformer zu übergeben, indem die Knoten manuell gesetzt werden.
def g(x):
"""Function to be approximated by periodic spline interpolation."""
return np.sin(x) - 0.7 * np.cos(x * 3)
y_train = g(x_train)
# Extend the test data into the future:
x_plot_ext = np.linspace(-1, 21, 200)
X_plot_ext = x_plot_ext[:, np.newaxis]
lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(color=["black", "tomato", "teal"])
ax.plot(x_plot_ext, g(x_plot_ext), linewidth=lw, label="ground truth")
ax.scatter(x_train, y_train, label="training points")
for transformer, label in [
(SplineTransformer(degree=3, n_knots=10), "spline"),
(
SplineTransformer(
degree=3,
knots=np.linspace(0, 2 * np.pi, 10)[:, None],
extrapolation="periodic",
),
"periodic spline",
),
]:
model = make_pipeline(transformer, Ridge(alpha=1e-3))
model.fit(X_train, y_train)
y_plot_ext = model.predict(X_plot_ext)
ax.plot(x_plot_ext, y_plot_ext, label=label)
ax.legend()
fig.show()
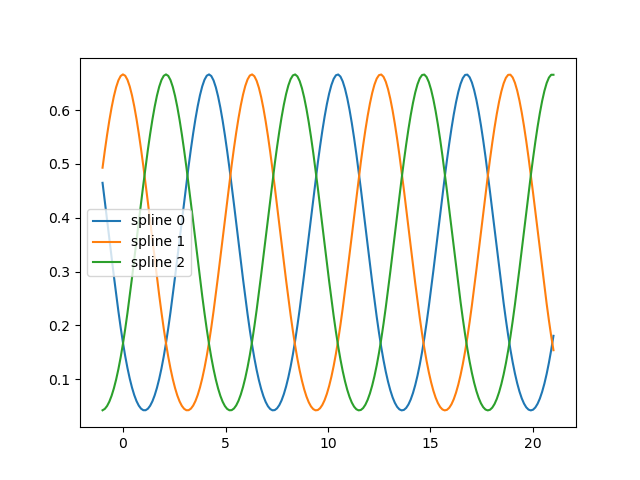
fig, ax = plt.subplots()
knots = np.linspace(0, 2 * np.pi, 4)
splt = SplineTransformer(knots=knots[:, None], degree=3, extrapolation="periodic").fit(
X_train
)
ax.plot(x_plot_ext, splt.transform(X_plot_ext))
ax.legend(ax.lines, [f"spline {n}" for n in range(3)])
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,348 Sekunden)
Verwandte Beispiele
Visualisierung der probabilistischen Vorhersagen eines VotingClassifier