Einzelner Schätzer im Vergleich zu Bagging: Bias-Varianz-Zerlegung

Dieses Beispiel veranschaulicht und vergleicht die Bias-Varianz-Zerlegung des erwarteten mittleren quadratischen Fehlers eines einzelnen Schätzers im Vergleich zu einem Bagging-Ensemble.

Bei der Regression kann der erwartete mittlere quadratische Fehler eines Schätzers in Bezug auf Bias, Varianz und Rauschen zerlegt werden. Im Durchschnitt über Datensätze des Regressionsproblems misst der Bias-Term den durchschnittlichen Betrag, um den sich die Vorhersagen des Schätzers von den Vorhersagen des bestmöglichen Schätzers für das Problem (d. h. des Bayes-Modells) unterscheiden. Der Varianzterm misst die Variabilität der Vorhersagen des Schätzers, wenn er über verschiedene zufällige Instanzen desselben Problems angepasst wird. Jede Probleminstanz wird im Folgenden als „LS“ für „Learning Sample“ bezeichnet. Schließlich misst das Rauschen den irreduziblen Teil des Fehlers, der auf die Variabilität in den Daten zurückzuführen ist.

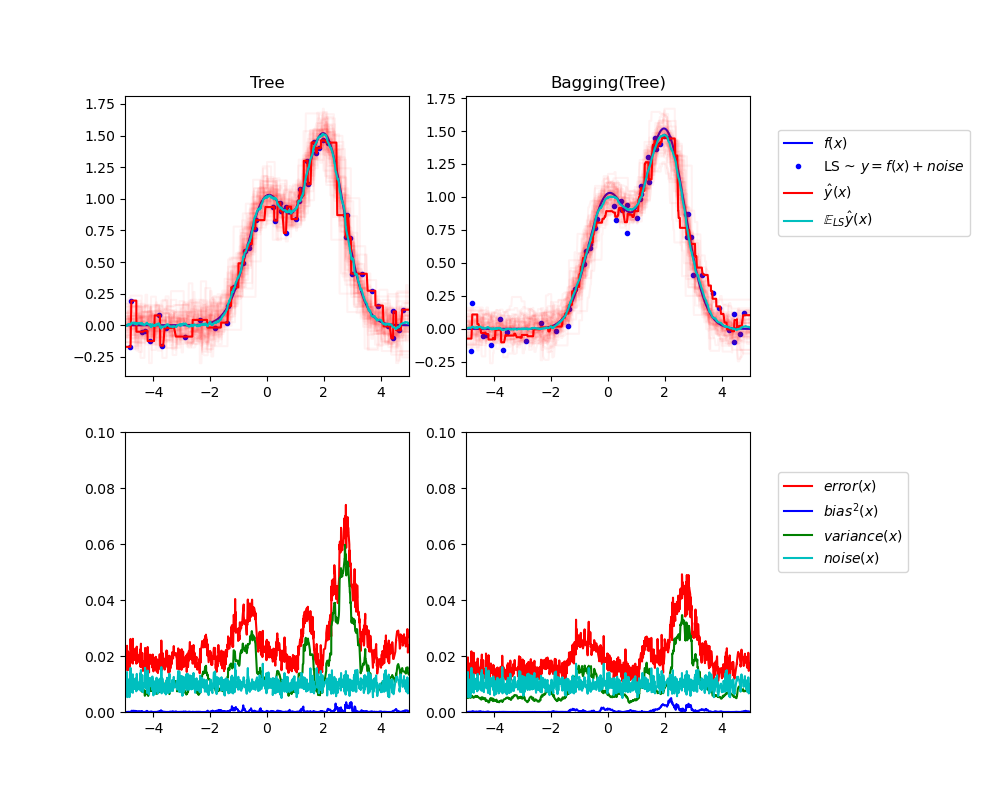
Die obere linke Abbildung zeigt die Vorhersagen (in Dunkelrot) eines einzelnen Entscheidungsbaums, der über einem zufälligen Datensatz LS (die blauen Punkte) eines Spiel-1D-Regressionsproblems trainiert wurde. Sie veranschaulicht auch die Vorhersagen (in Hellrot) anderer einzelner Entscheidungsbäume, die über anderen (und verschiedenen) zufällig gezogenen Instanzen LS des Problems trainiert wurden. Intuitiv entspricht der Varianzterm hier der Breite des Vorhersagestrahlers (in Hellrot) der einzelnen Schätzer. Je größer die Varianz, desto empfindlicher sind die Vorhersagen für x gegenüber kleinen Änderungen im Trainingsdatensatz. Der Bias-Term entspricht der Differenz zwischen der durchschnittlichen Vorhersage des Schätzers (in Cyan) und dem bestmöglichen Modell (in Dunkelblau). Bei diesem Problem können wir somit beobachten, dass der Bias ziemlich gering ist (sowohl die cyanfarbene als auch die blaue Kurve liegen nahe beieinander), während die Varianz groß ist (der rote Strahl ist ziemlich breit).

Die untere linke Abbildung stellt die punktweise Zerlegung des erwarteten mittleren quadratischen Fehlers eines einzelnen Entscheidungsbaums dar. Sie bestätigt, dass der Bias-Term (in Blau) gering ist, während die Varianz groß ist (in Grün). Sie veranschaulicht auch den Rauschteil des Fehlers, der wie erwartet konstant um 0.01 zu sein scheint.

Die rechten Abbildungen entsprechen denselben Diagrammen, jedoch unter Verwendung eines Bagging-Ensembles von Entscheidungsbäumen. In beiden Abbildungen können wir beobachten, dass der Bias-Term höher ist als im vorherigen Fall. In der oberen rechten Abbildung ist der Unterschied zwischen der durchschnittlichen Vorhersage (in Cyan) und dem bestmöglichen Modell größer (beachten Sie z. B. den Offset um x=2). In der unteren rechten Abbildung ist die Bias-Kurve ebenfalls etwas höher als in der unteren linken Abbildung. In Bezug auf die Varianz ist der Vorhersagestrahl jedoch schmaler, was auf eine geringere Varianz hindeutet. Tatsächlich ist, wie die untere rechte Abbildung bestätigt, der Varianzterm (in Grün) geringer als bei einzelnen Entscheidungsbäumen. Insgesamt ist die Bias-Varianz-Zerlegung daher nicht mehr dieselbe. Der Kompromiss ist für Bagging besser: Das Mitteln mehrerer auf Bootstrap-Kopien des Datensatzes angepasster Entscheidungsbäume erhöht den Bias-Term geringfügig, ermöglicht aber eine größere Reduzierung der Varianz, was zu einem niedrigeren gesamten mittleren quadratischen Fehler führt (vergleichen Sie die roten Kurven in den unteren Abbildungen). Die Skriptausgabe bestätigt ebenfalls diese Intuition. Der Gesamtfehler des Bagging-Ensembles ist geringer als der Gesamtfehler eines einzelnen Entscheidungsbaums, und dieser Unterschied ergibt sich tatsächlich hauptsächlich aus einer reduzierten Varianz.

Weitere Details zur Bias-Varianz-Zerlegung finden Sie in Abschnitt 7.3 von [1].

Referenzen

[1]

T. Hastie, R. Tibshirani und J. Friedman, „Elements of Statistical Learning“, Springer, 2009.

Tree: 0.0255 (error) = 0.0003 (bias^2)  + 0.0152 (var) + 0.0098 (noise)
Bagging(Tree): 0.0196 (error) = 0.0004 (bias^2)  + 0.0092 (var) + 0.0098 (noise)

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# Settings
n_repeat = 50  # Number of iterations for computing expectations
n_train = 50  # Size of the training set
n_test = 1000  # Size of the test set
noise = 0.1  # Standard deviation of the noise
np.random.seed(0)

# Change this for exploring the bias-variance decomposition of other
# estimators. This should work well for estimators with high variance (e.g.,
# decision trees or KNN), but poorly for estimators with low variance (e.g.,
# linear models).
estimators = [
    ("Tree", DecisionTreeRegressor()),
    ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor())),
]

n_estimators = len(estimators)


# Generate data
def f(x):
    x = x.ravel()

    return np.exp(-(x**2)) + 1.5 * np.exp(-((x - 2) ** 2))


def generate(n_samples, noise, n_repeat=1):
    X = np.random.rand(n_samples) * 10 - 5
    X = np.sort(X)

    if n_repeat == 1:
        y = f(X) + np.random.normal(0.0, noise, n_samples)
    else:
        y = np.zeros((n_samples, n_repeat))

        for i in range(n_repeat):
            y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

    X = X.reshape((n_samples, 1))

    return X, y


X_train = []
y_train = []

for i in range(n_repeat):
    X, y = generate(n_samples=n_train, noise=noise)
    X_train.append(X)
    y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# Loop over estimators to compare
for n, (name, estimator) in enumerate(estimators):
    # Compute predictions
    y_predict = np.zeros((n_test, n_repeat))

    for i in range(n_repeat):
        estimator.fit(X_train[i], y_train[i])
        y_predict[:, i] = estimator.predict(X_test)

    # Bias^2 + Variance + Noise decomposition of the mean squared error
    y_error = np.zeros(n_test)

    for i in range(n_repeat):
        for j in range(n_repeat):
            y_error += (y_test[:, j] - y_predict[:, i]) ** 2

    y_error /= n_repeat * n_repeat

    y_noise = np.var(y_test, axis=1)
    y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
    y_var = np.var(y_predict, axis=1)

    print(
        "{0}: {1:.4f} (error) = {2:.4f} (bias^2) "
        " + {3:.4f} (var) + {4:.4f} (noise)".format(
            name, np.mean(y_error), np.mean(y_bias), np.mean(y_var), np.mean(y_noise)
        )
    )

    # Plot figures
    plt.subplot(2, n_estimators, n + 1)
    plt.plot(X_test, f(X_test), "b", label="$f(x)$")
    plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

    for i in range(n_repeat):
        if i == 0:
            plt.plot(X_test, y_predict[:, i], "r", label=r"$\^y(x)$")
        else:
            plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

    plt.plot(X_test, np.mean(y_predict, axis=1), "c", label=r"$\mathbb{E}_{LS} \^y(x)$")

    plt.xlim([-5, 5])
    plt.title(name)

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

    plt.subplot(2, n_estimators, n_estimators + n + 1)
    plt.plot(X_test, y_error, "r", label="$error(x)$")
    plt.plot(X_test, y_bias, "b", label="$bias^2(x)$")
    plt.plot(X_test, y_var, "g", label="$variance(x)$")
    plt.plot(X_test, y_noise, "c", label="$noise(x)$")

    plt.xlim([-5, 5])
    plt.ylim([0, 0.1])

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

plt.subplots_adjust(right=0.75)
plt.show()

Verwandte Beispiele

Gewöhnliche kleinste Quadrate und Ridge Regression

Gewöhnliche kleinste Quadrate und Ridge Regression

Vergleich der Kalibrierung von Klassifikatoren

Vergleich der Kalibrierung von Klassifikatoren

Entscheidungsbaum-Regression

Entscheidungsbaum-Regression

Entscheidungsbaum-Regression mit AdaBoost

Entscheidungsbaum-Regression mit AdaBoost