Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Gaußsche Prozesse auf diskreten Datenstrukturen#
Dieses Beispiel veranschaulicht die Verwendung von Gaußschen Prozessen für Regressions- und Klassifikationsaufgaben auf Daten, die nicht in Form von Feature-Vektoren fester Länge vorliegen. Dies wird durch die Verwendung von Kernel-Funktionen erreicht, die direkt auf diskrete Strukturen wie Sequenzen variabler Länge, Bäume und Graphen operieren.
Insbesondere sind hier die Eingabevariablen einige Gen-Sequenzen, die als Strings variabler Länge gespeichert sind und aus den Buchstaben 'A', 'T', 'C' und 'G' bestehen, während die Ausgabevariablen Gleitkommazahlen und Wahr/Falsch-Labels bei den Regressions- bzw. Klassifikationsaufgaben sind.
Ein Kernel zwischen den Gen-Sequenzen wird mittels R-Konvolution [1] definiert, indem ein binärer buchstabenweiser Kernel über alle Buchstabenpaare einer Zeichenkette integriert wird.
Dieses Beispiel generiert drei Abbildungen.
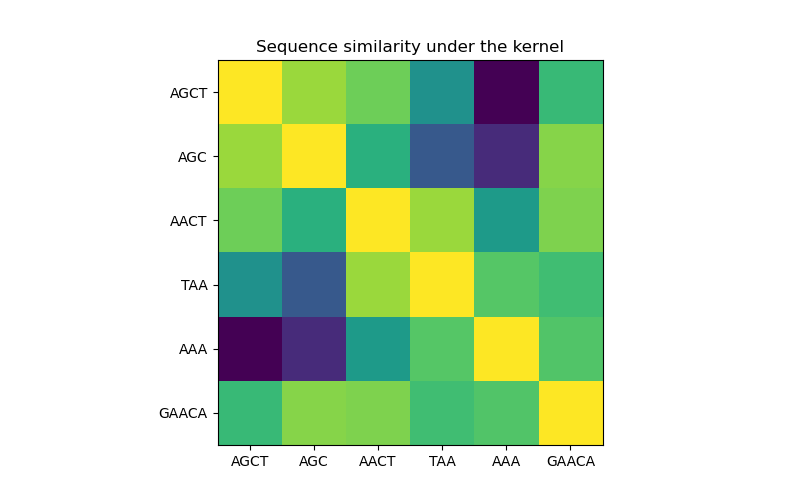
In der ersten Abbildung visualisieren wir den Wert des Kernels, d.h. die Ähnlichkeit der Sequenzen, mithilfe einer Farbskala. Eine hellere Farbe bedeutet hier eine höhere Ähnlichkeit.
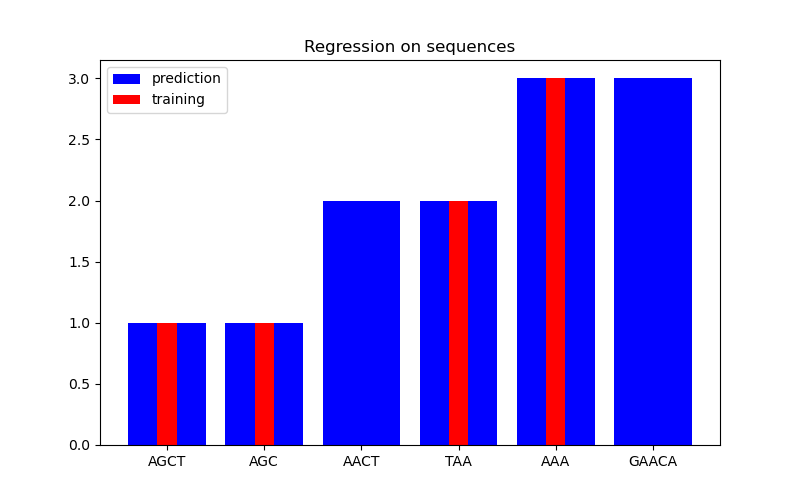
In der zweiten Abbildung zeigen wir einige Regressionsergebnisse auf einem Datensatz von 6 Sequenzen. Hier verwenden wir die 1., 2., 4. und 5. Sequenz als Trainingsmenge, um Vorhersagen für die 3. und 6. Sequenz zu treffen.
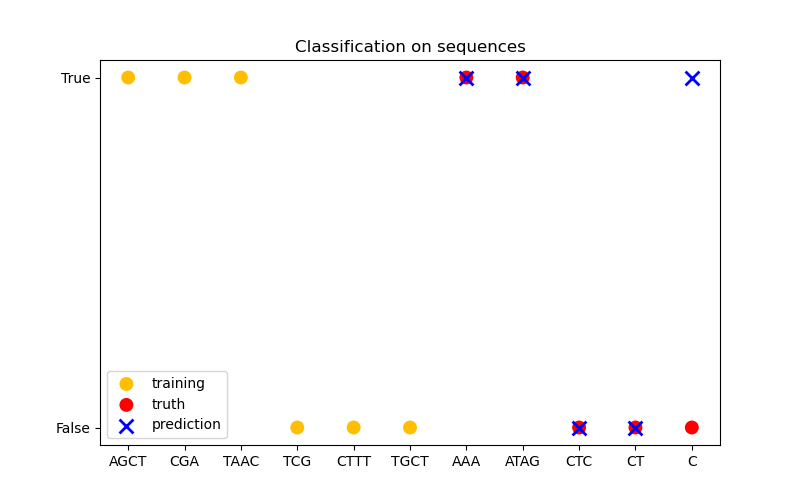
In der dritten Abbildung demonstrieren wir ein Klassifikationsmodell, indem wir 6 Sequenzen trainieren und Vorhersagen für weitere 5 Sequenzen treffen. Die Ground Truth ist hier einfach, ob mindestens ein 'A' in der Sequenz vorhanden ist. Hier trifft das Modell vier korrekte Klassifikationen und scheitert bei einer.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from sklearn.base import clone
from sklearn.gaussian_process import GaussianProcessClassifier, GaussianProcessRegressor
from sklearn.gaussian_process.kernels import GenericKernelMixin, Hyperparameter, Kernel
class SequenceKernel(GenericKernelMixin, Kernel):
"""
A minimal (but valid) convolutional kernel for sequences of variable
lengths."""
def __init__(self, baseline_similarity=0.5, baseline_similarity_bounds=(1e-5, 1)):
self.baseline_similarity = baseline_similarity
self.baseline_similarity_bounds = baseline_similarity_bounds
@property
def hyperparameter_baseline_similarity(self):
return Hyperparameter(
"baseline_similarity", "numeric", self.baseline_similarity_bounds
)
def _f(self, s1, s2):
"""
kernel value between a pair of sequences
"""
return sum(
[1.0 if c1 == c2 else self.baseline_similarity for c1 in s1 for c2 in s2]
)
def _g(self, s1, s2):
"""
kernel derivative between a pair of sequences
"""
return sum([0.0 if c1 == c2 else 1.0 for c1 in s1 for c2 in s2])
def __call__(self, X, Y=None, eval_gradient=False):
if Y is None:
Y = X
if eval_gradient:
return (
np.array([[self._f(x, y) for y in Y] for x in X]),
np.array([[[self._g(x, y)] for y in Y] for x in X]),
)
else:
return np.array([[self._f(x, y) for y in Y] for x in X])
def diag(self, X):
return np.array([self._f(x, x) for x in X])
def is_stationary(self):
return False
def clone_with_theta(self, theta):
cloned = clone(self)
cloned.theta = theta
return cloned
kernel = SequenceKernel()
Sequenzähnlichkeitsmatrix unter dem Kernel#
import matplotlib.pyplot as plt
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
K = kernel(X)
D = kernel.diag(X)
plt.figure(figsize=(8, 5))
plt.imshow(np.diag(D**-0.5).dot(K).dot(np.diag(D**-0.5)))
plt.xticks(np.arange(len(X)), X)
plt.yticks(np.arange(len(X)), X)
plt.title("Sequence similarity under the kernel")
plt.show()
Regression#
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
Y = np.array([1.0, 1.0, 2.0, 2.0, 3.0, 3.0])
training_idx = [0, 1, 3, 4]
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(X[training_idx], Y[training_idx])
plt.figure(figsize=(8, 5))
plt.bar(np.arange(len(X)), gp.predict(X), color="b", label="prediction")
plt.bar(training_idx, Y[training_idx], width=0.2, color="r", alpha=1, label="training")
plt.xticks(np.arange(len(X)), X)
plt.title("Regression on sequences")
plt.legend()
plt.show()
Klassifizierung#
X_train = np.array(["AGCT", "CGA", "TAAC", "TCG", "CTTT", "TGCT"])
# whether there are 'A's in the sequence
Y_train = np.array([True, True, True, False, False, False])
gp = GaussianProcessClassifier(kernel)
gp.fit(X_train, Y_train)
X_test = ["AAA", "ATAG", "CTC", "CT", "C"]
Y_test = [True, True, False, False, False]
plt.figure(figsize=(8, 5))
plt.scatter(
np.arange(len(X_train)),
[1.0 if c else -1.0 for c in Y_train],
s=100,
marker="o",
edgecolor="none",
facecolor=(1, 0.75, 0),
label="training",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in Y_test],
s=100,
marker="o",
edgecolor="none",
facecolor="r",
label="truth",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in gp.predict(X_test)],
s=100,
marker="x",
facecolor="b",
linewidth=2,
label="prediction",
)
plt.xticks(np.arange(len(X_train) + len(X_test)), np.concatenate((X_train, X_test)))
plt.yticks([-1, 1], [False, True])
plt.title("Classification on sequences")
plt.legend()
plt.show()
/home/circleci/project/sklearn/gaussian_process/kernels.py:440: ConvergenceWarning:
The optimal value found for dimension 0 of parameter baseline_similarity is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
Gesamtlaufzeit des Skripts: (0 Minuten 0.165 Sekunden)
Verwandte Beispiele
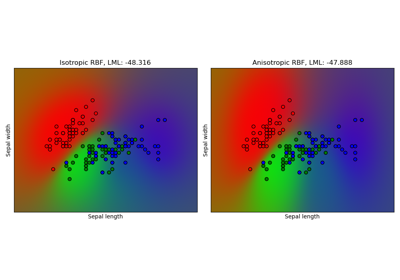
Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz
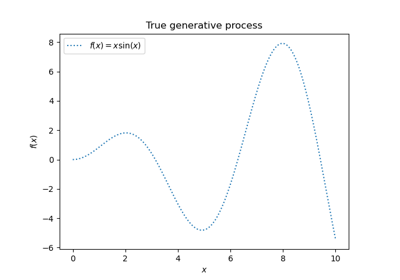
Gauß-Prozesse Regression: grundlegendes Einführungsexempel