Test mit Permutationen die Signifikanz eines Klassifizierungsergebnisses

Dieses Beispiel demonstriert die Verwendung von permutation_test_score, um die Signifikanz eines kreuzvalidierten Ergebnisses mittels Permutationen zu bewerten.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatz

Wir werden den Iris-Pflanzen-Datensatz verwenden, der Messungen von 3 Iris-Arten enthält. Unser Modell wird die Messungen verwenden, um die Iris-Art vorherzusagen.

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

Zum Vergleich generieren wir auch einige zufällige Merkmalsdaten (d. h. 20 Merkmale), die nicht mit den Klassenlabels im Iris-Datensatz korreliert sind.

import numpy as np

n_uncorrelated_features = 20
rng = np.random.RandomState(seed=0)
# Use same number of samples as in iris and 20 features
X_rand = rng.normal(size=(X.shape[0], n_uncorrelated_features))

Permutationstest-Ergebnis

Als Nächstes berechnen wir das permutation_test_score sowohl für den ursprünglichen Iris-Datensatz (bei dem eine starke Beziehung zwischen Merkmalen und Labels besteht) als auch für die zufällig generierten Merkmale mit Iris-Labels (bei denen keine Abhängigkeit zwischen Merkmalen und Labels erwartet wird). Wir verwenden den SVC-Klassifikator und die Genauigkeitsbewertung, um das Modell in jeder Runde zu bewerten.

permutation_test_score generiert eine Nullverteilung, indem die Genauigkeit des Klassifikators auf 1000 verschiedenen Permutationen des Datensatzes berechnet wird, wobei die Merkmale gleich bleiben, aber die Labels unterschiedlichen zufälligen Permutationen unterzogen werden. Dies ist die Verteilung für die Nullhypothese, die besagt, dass keine Abhängigkeit zwischen Merkmalen und Labels besteht. Ein empirischer p-Wert wird dann als der Anteil der Permutationen berechnet, für die das vom Modell auf der Permutation trainierte Ergebnis größer oder gleich dem Ergebnis ist, das mit den Originaldaten erzielt wurde.

from sklearn.model_selection import StratifiedKFold, permutation_test_score
from sklearn.svm import SVC

clf = SVC(kernel="linear", random_state=7)
cv = StratifiedKFold(n_splits=2, shuffle=True, random_state=0)

score_iris, perm_scores_iris, pvalue_iris = permutation_test_score(
    clf, X, y, scoring="accuracy", cv=cv, n_permutations=1000
)

score_rand, perm_scores_rand, pvalue_rand = permutation_test_score(
    clf, X_rand, y, scoring="accuracy", cv=cv, n_permutations=1000
)

Originaldaten

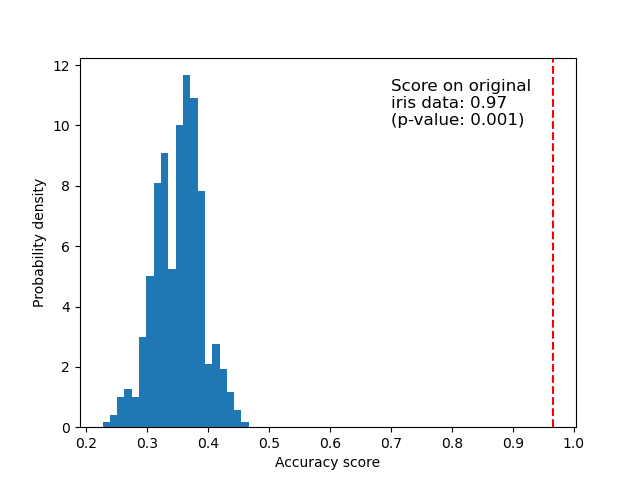
Unten wird ein Histogramm der Permutationsergebnisse (der Nullverteilung) geplottet. Die rote Linie zeigt das Ergebnis des Klassifikators auf den Originaldaten (ohne permutierte Labels). Das Ergebnis ist viel besser als die Ergebnisse, die durch die Verwendung permutierter Daten erzielt wurden, und der p-Wert ist daher sehr niedrig. Dies deutet darauf hin, dass die Wahrscheinlichkeit, dass ein so gutes Ergebnis zufällig erzielt wird, gering ist. Es liefert einen Beweis dafür, dass der Iris-Datensatz eine echte Abhängigkeit zwischen Merkmalen und Labels enthält und der Klassifikator diese nutzen konnte, um gute Ergebnisse zu erzielen. Der niedrige p-Wert kann dazu führen, dass wir die Nullhypothese verwerfen.

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.hist(perm_scores_iris, bins=20, density=True)
ax.axvline(score_iris, ls="--", color="r")
score_label = (
    f"Score on original\niris data: {score_iris:.2f}\n(p-value: {pvalue_iris:.3f})"
)
ax.text(0.7, 10, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
_ = ax.set_ylabel("Probability density")

Zufallsdaten

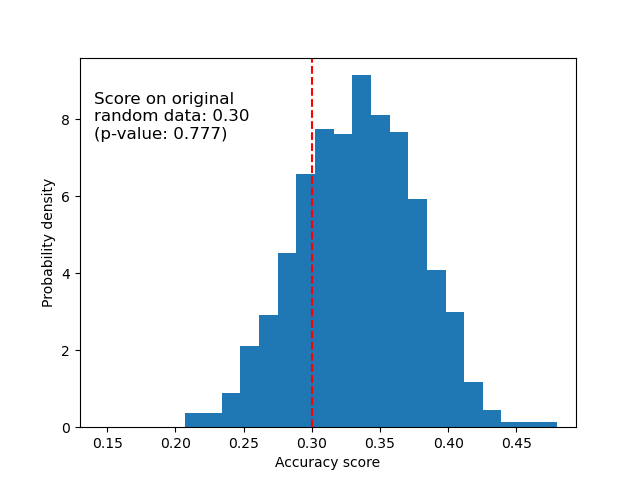
Unten wird die Nullverteilung für die randomisierten Daten geplottet. Die Permutationsergebnisse sind denen ähnlich, die mit dem ursprünglichen Iris-Datensatz erzielt wurden, da die Permutation immer eine vorhandene Merkmals-Label-Abhängigkeit zerstört. Das Ergebnis, das in diesem Fall mit den randomisierten Daten erzielt wird, ist jedoch sehr schlecht. Dies führt zu einem großen p-Wert, was bestätigt, dass in den randomisierten Daten keine Merkmals-Label-Abhängigkeit vorhanden war.

fig, ax = plt.subplots()

ax.hist(perm_scores_rand, bins=20, density=True)
ax.set_xlim(0.13)
ax.axvline(score_rand, ls="--", color="r")
score_label = (
    f"Score on original\nrandom data: {score_rand:.2f}\n(p-value: {pvalue_rand:.3f})"
)
ax.text(0.14, 7.5, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
ax.set_ylabel("Probability density")
plt.show()

Ein weiterer möglicher Grund für einen hohen p-Wert könnte sein, dass der Klassifikator die Struktur in den Daten nicht nutzen konnte. In diesem Fall wäre der p-Wert nur für Klassifikatoren niedrig, die die vorhandene Abhängigkeit nutzen können. In unserem obigen Fall, wo die Daten zufällig sind, hätten alle Klassifikatoren einen hohen p-Wert, da keine Struktur in den Daten vorhanden ist. Wir könnten die Nullhypothese möglicherweise verwerfen oder auch nicht, je nachdem, ob der p-Wert auch bei einem besser geeigneten Schätzer hoch ist.

Abschließend sei darauf hingewiesen, dass dieser Test selbst bei nur schwacher Struktur in den Daten niedrige p-Werte ergibt [1].

Referenzen

[1]

Ojala und Garriga. Permutation Tests for Studying Classifier Performance. The Journal of Machine Learning Research (2010) vol. 11

Verwandte Beispiele

Principal Component Analysis (PCA) auf dem Iris-Datensatz

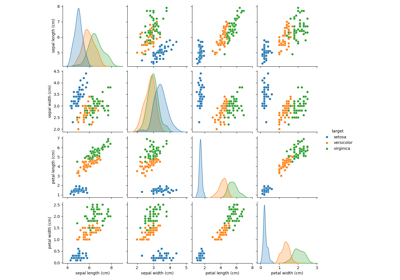
Principal Component Analysis (PCA) auf dem Iris-Datensatz

Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten

Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

Inkrementelles PCA

Inkrementelles PCA