Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel direkt in Ihrem Browser über JupyterLite oder Binder auszuführen.
Statistischer Vergleich von Modellen mittels Grid Search#
Dieses Beispiel veranschaulicht, wie die Leistung von Modellen, die trainiert und bewertet wurden, mittels GridSearchCV statistisch verglichen werden kann.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Wir beginnen mit der Simulation von Mond-förmigen Daten (bei denen die ideale Trennung zwischen den Klassen nicht-linear ist) und fügen einen moderaten Grad an Rauschen hinzu. Die Datenpunkte gehören zu einer von zwei möglichen Klassen, die anhand von zwei Merkmalen vorhergesagt werden sollen. Wir simulieren 50 Stichproben für jede Klasse.
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_moons
X, y = make_moons(noise=0.352, random_state=1, n_samples=100)
sns.scatterplot(
x=X[:, 0], y=X[:, 1], hue=y, marker="o", s=25, edgecolor="k", legend=False
).set_title("Data")
plt.show()

Wir werden die Leistung von SVC-Estimators vergleichen, die in ihrem kernel-Parameter variieren, um zu entscheiden, welche Wahl dieses Hyperparameters unsere simulierten Daten am besten vorhersagt. Wir werden die Leistung der Modelle mit RepeatedStratifiedKFold bewerten, wobei wir eine 10-fache stratifizierte Kreuzvalidierung 10 Mal wiederholen, wobei bei jeder Wiederholung eine andere Zufallszuordnung der Daten verwendet wird. Die Leistung wird mit roc_auc_score bewertet.
from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.svm import SVC
param_grid = [
{"kernel": ["linear"]},
{"kernel": ["poly"], "degree": [2, 3]},
{"kernel": ["rbf"]},
]
svc = SVC(random_state=0)
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=10, random_state=0)
search = GridSearchCV(estimator=svc, param_grid=param_grid, scoring="roc_auc", cv=cv)
search.fit(X, y)
Wir können nun die Ergebnisse unserer Suche inspizieren, sortiert nach ihrem mean_test_score
import pandas as pd
results_df = pd.DataFrame(search.cv_results_)
results_df = results_df.sort_values(by=["rank_test_score"])
results_df = results_df.set_index(
results_df["params"].apply(lambda x: "_".join(str(val) for val in x.values()))
).rename_axis("kernel")
results_df[["params", "rank_test_score", "mean_test_score", "std_test_score"]]
Wir sehen, dass der Estimator mit dem 'rbf'-Kernel die beste Leistung erbrachte, dicht gefolgt von 'linear'. Beide Estimators mit einem 'poly'-Kernel zeigten eine schlechtere Leistung, wobei der mit einem polynomialen Grad von zwei eine deutlich geringere Leistung als alle anderen Modelle erreichte.
Normalerweise endet die Analyse hier, aber die Hälfte der Geschichte fehlt. Die Ausgabe von GridSearchCV liefert keine Informationen über die Sicherheit der Unterschiede zwischen den Modellen. Wir wissen nicht, ob diese **statistisch** signifikant sind. Um dies zu bewerten, müssen wir einen statistischen Test durchführen. Insbesondere zum Kontrastieren der Leistung zweier Modelle sollten wir ihre AUC-Scores statistisch vergleichen. Es gibt 100 Stichproben (AUC-Scores) für jedes Modell, da wir eine 10-fache Kreuzvalidierung 10 Mal wiederholt haben.
Die Scores der Modelle sind jedoch nicht unabhängig: Alle Modelle werden auf den **gleichen** 100 Partitionen bewertet, was die Korrelation zwischen der Leistung der Modelle erhöht. Da einige Partitionen der Daten die Unterscheidung der Klassen für alle Modelle besonders einfach oder schwierig machen können, variieren die Modell-Scores gemeinsam.
Betrachten wir diesen Partizipationseffekt, indem wir die Leistung aller Modelle in jeder Faltung auftragen und die Korrelation zwischen den Modellen über die Faltungen hinweg berechnen.
# create df of model scores ordered by performance
model_scores = results_df.filter(regex=r"split\d*_test_score")
# plot 30 examples of dependency between cv fold and AUC scores
fig, ax = plt.subplots()
sns.lineplot(
data=model_scores.transpose().iloc[:30],
dashes=False,
palette="Set1",
marker="o",
alpha=0.5,
ax=ax,
)
ax.set_xlabel("CV test fold", size=12, labelpad=10)
ax.set_ylabel("Model AUC", size=12)
ax.tick_params(bottom=True, labelbottom=False)
plt.show()
# print correlation of AUC scores across folds
print(f"Correlation of models:\n {model_scores.transpose().corr()}")

Correlation of models:
kernel rbf linear 3_poly 2_poly
kernel
rbf 1.000000 0.882561 0.783392 0.351390
linear 0.882561 1.000000 0.746492 0.298688
3_poly 0.783392 0.746492 1.000000 0.355440
2_poly 0.351390 0.298688 0.355440 1.000000
Wir können beobachten, dass die Leistung der Modelle stark von der Faltung abhängt.
Folglich werden wir bei Annahme von Unabhängigkeit zwischen Stichproben die in unseren statistischen Tests berechnete Varianz unterschätzen und die Anzahl der falsch positiven Fehler erhöhen (d. h. einen signifikanten Unterschied zwischen Modellen feststellen, obwohl keiner existiert) [1].
Für diese Fälle wurden mehrere variantenkorrigierte statistische Tests entwickelt. In diesem Beispiel zeigen wir, wie einer davon (der sogenannte Nadeau- und Bengio-korrigierte t-Test) unter zwei verschiedenen statistischen Rahmenwerken implementiert wird: frequentistisch und bayesianisch.
Vergleich zweier Modelle: frequentistischer Ansatz#
Wir können zunächst fragen: "Ist das erste Modell signifikant besser als das zweite Modell (wenn nach mean_test_score sortiert)?"
Um diese Frage mit einem frequentistischen Ansatz zu beantworten, könnten wir einen gepaarten t-Test durchführen und den p-Wert berechnen. Dies ist in der Prognoseliteratur auch als Diebold-Mariano-Test bekannt [5]. Viele Varianten eines solchen t-Tests wurden entwickelt, um das 'Problem der Nichtunabhängigkeit von Stichproben', das im vorherigen Abschnitt beschrieben wurde, zu berücksichtigen. Wir verwenden die Variante, die sich als die höchste Replizierbarkeit (die bewertet, wie ähnlich die Leistung eines Modells bei der Bewertung auf verschiedenen zufälligen Partitionen desselben Datensatzes ist) erwiesen hat, während sie gleichzeitig eine niedrige Rate an falsch positiven und falsch negativen Fehlern aufweist: den Nadeau- und Bengio-korrigierten t-Test [2], der eine 10-mal wiederholte 10-fache Kreuzvalidierung verwendet [3].
Dieser korrigierte gepaarte t-Test wird berechnet als
wobei \(k\) die Anzahl der Faltungen, \(r\) die Anzahl der Wiederholungen in der Kreuzvalidierung, \(x\) die Differenz der Leistungen der Modelle, \(n_{test}\) die Anzahl der für das Testen verwendeten Stichproben, \(n_{train}\) die Anzahl der für das Trainieren verwendeten Stichproben und \(\hat{\sigma}^2\) die Varianz der beobachteten Unterschiede darstellt.
Implementieren wir einen korrigierten rechtsseitigen gepaarten t-Test, um zu bewerten, ob die Leistung des ersten Modells signifikant besser ist als die des zweiten Modells. Unsere Nullhypothese ist, dass das zweite Modell mindestens so gut abschneidet wie das erste Modell.
import numpy as np
from scipy.stats import t
def corrected_std(differences, n_train, n_test):
"""Corrects standard deviation using Nadeau and Bengio's approach.
Parameters
----------
differences : ndarray of shape (n_samples,)
Vector containing the differences in the score metrics of two models.
n_train : int
Number of samples in the training set.
n_test : int
Number of samples in the testing set.
Returns
-------
corrected_std : float
Variance-corrected standard deviation of the set of differences.
"""
# kr = k times r, r times repeated k-fold crossvalidation,
# kr equals the number of times the model was evaluated
kr = len(differences)
corrected_var = np.var(differences, ddof=1) * (1 / kr + n_test / n_train)
corrected_std = np.sqrt(corrected_var)
return corrected_std
def compute_corrected_ttest(differences, df, n_train, n_test):
"""Computes right-tailed paired t-test with corrected variance.
Parameters
----------
differences : array-like of shape (n_samples,)
Vector containing the differences in the score metrics of two models.
df : int
Degrees of freedom.
n_train : int
Number of samples in the training set.
n_test : int
Number of samples in the testing set.
Returns
-------
t_stat : float
Variance-corrected t-statistic.
p_val : float
Variance-corrected p-value.
"""
mean = np.mean(differences)
std = corrected_std(differences, n_train, n_test)
t_stat = mean / std
p_val = t.sf(np.abs(t_stat), df) # right-tailed t-test
return t_stat, p_val
model_1_scores = model_scores.iloc[0].values # scores of the best model
model_2_scores = model_scores.iloc[1].values # scores of the second-best model
differences = model_1_scores - model_2_scores
n = differences.shape[0] # number of test sets
df = n - 1
n_train = len(next(iter(cv.split(X, y)))[0])
n_test = len(next(iter(cv.split(X, y)))[1])
t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
print(f"Corrected t-value: {t_stat:.3f}\nCorrected p-value: {p_val:.3f}")
Corrected t-value: 0.750
Corrected p-value: 0.227
Wir können die korrigierten t- und p-Werte mit den unkorrigierten vergleichen.
Uncorrected t-value: 2.611
Uncorrected p-value: 0.005
Bei Verwendung des konventionellen Signifikanzniveaus alpha von p=0.05 beobachten wir, dass der unkorrigierte t-Test zu dem Schluss kommt, dass das erste Modell signifikant besser ist als das zweite.
Mit dem korrigierten Ansatz können wir diesen Unterschied dagegen nicht feststellen.
Im letzteren Fall erlaubt uns der frequentistische Ansatz jedoch nicht zu schlussfolgern, dass das erste und das zweite Modell eine äquivalente Leistung aufweisen. Wenn wir diese Behauptung aufstellen wollen, müssen wir einen bayesianischen Ansatz verwenden.
Vergleich zweier Modelle: Bayesischer Ansatz#
Wir können die bayesianische Schätzung verwenden, um die Wahrscheinlichkeit zu berechnen, dass das erste Modell besser ist als das zweite. Die bayesianische Schätzung gibt eine Verteilung aus, gefolgt von dem Mittelwert \(\mu\) der Unterschiede in der Leistung zweier Modelle.
Um die Posterior-Verteilung zu erhalten, müssen wir einen Prior definieren, der unsere Überzeugungen darüber modelliert, wie der Mittelwert verteilt ist, bevor wir die Daten betrachten, und ihn mit einer Likelihood-Funktion multiplizieren, die berechnet, wie wahrscheinlich unsere beobachteten Unterschiede sind, gegeben die Werte, die der Mittelwert der Unterschiede annehmen könnte.
Die bayesianische Schätzung kann in vielerlei Hinsicht durchgeführt werden, um unsere Frage zu beantworten, aber in diesem Beispiel implementieren wir den Ansatz, der von Benavoli und Kollegen vorgeschlagen wurde [4].
Eine Möglichkeit, unseren Posterior mit einem geschlossenen Ausdruck zu definieren, besteht darin, einen Prior zu wählen, der konjugiert zur Likelihood-Funktion ist. Benavoli und Kollegen [4] zeigen, dass wir beim Vergleich der Leistung zweier Klassifikatoren den Prior als Normal-Gamma-Verteilung (mit unbekanntem Mittelwert und unbekannter Varianz) modellieren können, die konjugiert zu einer Normal-Likelihood ist, um so den Posterior als Normalverteilung auszudrücken. Durch Marginalisierung der Varianz aus diesem normalen Posterior definieren wir den Posterior des Mittelwertparameters als Student-t-Verteilung. Spezifisch
wobei \(n\) die Gesamtzahl der Stichproben, \(\overline{x}\) den mittleren Unterschied der Scores darstellt, \(n_{test}\) die Anzahl der für das Testen verwendeten Stichproben, \(n_{train}\) die Anzahl der für das Trainieren verwendeten Stichproben und \(\hat{\sigma}^2\) die Varianz der beobachteten Unterschiede darstellt.
Beachten Sie, dass wir auch in unserem bayesianischen Ansatz die Nadeau- und Bengio-korrigierte Varianz verwenden.
Berechnen und plotten wir den Posterior.
Plotten wir die Posterior-Verteilung.
x = np.linspace(t_post.ppf(0.001), t_post.ppf(0.999), 100)
plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.fill_between(x, t_post.pdf(x), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution")
plt.show()

Wir können die Wahrscheinlichkeit, dass das erste Modell besser ist als das zweite, berechnen, indem wir die Fläche unter der Kurve der Posterior-Verteilung von Null bis unendlich berechnen. Und auch umgekehrt: Wir können die Wahrscheinlichkeit berechnen, dass das zweite Modell besser ist als das erste, indem wir die Fläche unter der Kurve von minus unendlich bis Null berechnen.
better_prob = 1 - t_post.cdf(0)
print(
f"Probability of {model_scores.index[0]} being more accurate than "
f"{model_scores.index[1]}: {better_prob:.3f}"
)
print(
f"Probability of {model_scores.index[1]} being more accurate than "
f"{model_scores.index[0]}: {1 - better_prob:.3f}"
)
Probability of rbf being more accurate than linear: 0.773
Probability of linear being more accurate than rbf: 0.227
Im Gegensatz zum frequentistischen Ansatz können wir die Wahrscheinlichkeit berechnen, dass ein Modell besser ist als das andere.
Beachten Sie, dass wir ähnliche Ergebnisse wie im frequentistischen Ansatz erzielt haben. Aufgrund unserer Wahl der Prioren führen wir im Wesentlichen die gleichen Berechnungen durch, dürfen aber unterschiedliche Aussagen treffen.
Region of Practical Equivalence#
Manchmal sind wir daran interessiert, die Wahrscheinlichkeiten zu bestimmen, dass unsere Modelle eine äquivalente Leistung aufweisen, wobei "äquivalent" auf praktische Weise definiert wird. Ein naiver Ansatz [4] wäre, Estimators als praktisch äquivalent zu definieren, wenn sie sich um weniger als 1 % in ihrer Genauigkeit unterscheiden. Wir könnten diese praktische Äquivalenz aber auch unter Berücksichtigung des zu lösenden Problems definieren. Zum Beispiel würde ein Unterschied von 5 % in der Genauigkeit einen Anstieg von 1000 $ im Umsatz bedeuten, und jede darüber hinausgehende Menge betrachten wir als relevant für unser Geschäft.
In diesem Beispiel definieren wir die Region of Practical Equivalence (ROPE) als \([-0.01, 0.01]\). Das heißt, wir betrachten zwei Modelle als praktisch äquivalent, wenn sie sich in ihrer Leistung um weniger als 1 % unterscheiden.
Um die Wahrscheinlichkeiten für praktisch äquivalente Klassifikatoren zu berechnen, berechnen wir die Fläche unter der Kurve des Posterior über das ROPE-Intervall.
rope_interval = [-0.01, 0.01]
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])
print(
f"Probability of {model_scores.index[0]} and {model_scores.index[1]} "
f"being practically equivalent: {rope_prob:.3f}"
)
Probability of rbf and linear being practically equivalent: 0.432
Wir können plotten, wie sich der Posterior über das ROPE-Intervall verteilt.
x_rope = np.linspace(rope_interval[0], rope_interval[1], 100)
plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.vlines([-0.01, 0.01], ymin=0, ymax=(np.max(t_post.pdf(x)) + 1))
plt.fill_between(x_rope, t_post.pdf(x_rope), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution under the ROPE")
plt.show()

Wie in [4] vorgeschlagen, können wir diese Wahrscheinlichkeiten anhand der gleichen Kriterien wie im frequentistischen Ansatz interpretieren: Ist die Wahrscheinlichkeit, innerhalb des ROPE zu liegen, größer als 95 % (Alpha-Wert von 5 %)? In diesem Fall können wir schlussfolgern, dass beide Modelle praktisch äquivalent sind.
Der bayesianische Schätzansatz ermöglicht es uns auch, zu berechnen, wie unsicher wir uns über unsere Schätzung der Differenz sind. Dies kann anhand von Glaubwürdigkeitsintervallen berechnet werden. Für eine gegebene Wahrscheinlichkeit zeigen sie den Bereich von Werten, den die geschätzte Größe, in unserem Fall die mittlere Leistungsdifferenz zwischen den Modellen, annehmen kann. Zum Beispiel sagt ein 50 % Glaubwürdigkeitsintervall [x, y] aus, dass mit 50 % Wahrscheinlichkeit die wahre (mittlere) Leistungsdifferenz zwischen den Modellen zwischen x und y liegt.
Ermitteln wir die Glaubwürdigkeitsintervalle unserer Daten mit 50 %, 75 % und 95 %.
cred_intervals = []
intervals = [0.5, 0.75, 0.95]
for interval in intervals:
cred_interval = list(t_post.interval(interval))
cred_intervals.append([interval, cred_interval[0], cred_interval[1]])
cred_int_df = pd.DataFrame(
cred_intervals, columns=["interval", "lower value", "upper value"]
).set_index("interval")
cred_int_df
Wie in der Tabelle gezeigt, besteht eine 50%ige Wahrscheinlichkeit, dass die tatsächliche mittlere Differenz zwischen den Modellen zwischen 0,000977 und 0,019023 liegt, eine 70%ige Wahrscheinlichkeit, dass sie zwischen -0,005422 und 0,025422 liegt, und eine 95%ige Wahrscheinlichkeit, dass sie zwischen -0,016445 und 0,036445 liegt.
Paarweiser Vergleich aller Modelle: frequentistischer Ansatz#
Wir könnten auch daran interessiert sein, die Leistung aller unserer Modelle, die mit GridSearchCV bewertet wurden, zu vergleichen. In diesem Fall würden wir unseren statistischen Test mehrmals durchführen, was uns zum Problem des Mehrfachvergleichs führt.
Es gibt viele mögliche Wege, dieses Problem anzugehen, aber ein Standardansatz ist die Anwendung einer Bonferroni-Korrektur. Bonferroni kann berechnet werden, indem der p-Wert mit der Anzahl der verglichenen Vergleiche multipliziert wird.
Vergleichen wir die Leistung der Modelle mithilfe des korrigierten t-Tests.
from itertools import combinations
from math import factorial
n_comparisons = factorial(len(model_scores)) / (
factorial(2) * factorial(len(model_scores) - 2)
)
pairwise_t_test = []
for model_i, model_k in combinations(range(len(model_scores)), 2):
model_i_scores = model_scores.iloc[model_i].values
model_k_scores = model_scores.iloc[model_k].values
differences = model_i_scores - model_k_scores
t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
p_val *= n_comparisons # implement Bonferroni correction
# Bonferroni can output p-values higher than 1
p_val = 1 if p_val > 1 else p_val
pairwise_t_test.append(
[model_scores.index[model_i], model_scores.index[model_k], t_stat, p_val]
)
pairwise_comp_df = pd.DataFrame(
pairwise_t_test, columns=["model_1", "model_2", "t_stat", "p_val"]
).round(3)
pairwise_comp_df
Wir beobachten, dass nach der Korrektur für Mehrfachvergleiche das einzige Modell, das sich signifikant von den anderen unterscheidet, '2_poly' ist. 'rbf', das von GridSearchCV an erster Stelle eingestufte Modell, unterscheidet sich nicht signifikant von 'linear' oder '3_poly'.
Paarweiser Vergleich aller Modelle: Bayesischer Ansatz#
Bei der Verwendung der bayesianischen Schätzung zum Vergleich mehrerer Modelle müssen wir keine Korrektur für Mehrfachvergleiche vornehmen (Gründe hierfür siehe [4]).
Wir können unsere paarweisen Vergleiche auf die gleiche Weise durchführen wie im ersten Abschnitt.
pairwise_bayesian = []
for model_i, model_k in combinations(range(len(model_scores)), 2):
model_i_scores = model_scores.iloc[model_i].values
model_k_scores = model_scores.iloc[model_k].values
differences = model_i_scores - model_k_scores
t_post = t(
df, loc=np.mean(differences), scale=corrected_std(differences, n_train, n_test)
)
worse_prob = t_post.cdf(rope_interval[0])
better_prob = 1 - t_post.cdf(rope_interval[1])
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])
pairwise_bayesian.append([worse_prob, better_prob, rope_prob])
pairwise_bayesian_df = pd.DataFrame(
pairwise_bayesian, columns=["worse_prob", "better_prob", "rope_prob"]
).round(3)
pairwise_comp_df = pairwise_comp_df.join(pairwise_bayesian_df)
pairwise_comp_df
Mit dem bayesianischen Ansatz können wir die Wahrscheinlichkeit berechnen, dass ein Modell besser, schlechter oder praktisch äquivalent zu einem anderen ist.
Die Ergebnisse zeigen, dass das von GridSearchCV an erster Stelle eingestufte Modell 'rbf' eine Wahrscheinlichkeit von etwa 6,8 % hat, schlechter als 'linear' zu sein, und eine Wahrscheinlichkeit von 1,8 %, schlechter als '3_poly' zu sein. 'rbf' und 'linear' haben eine 43%ige Wahrscheinlichkeit, praktisch äquivalent zu sein, während 'rbf' und '3_poly' eine 10%ige Chance dazu haben.
Ähnlich wie bei den mit dem frequentistischen Ansatz erzielten Schlussfolgerungen haben alle Modelle eine 100%ige Wahrscheinlichkeit, besser als '2_poly' zu sein, und keines hat eine praktisch äquivalente Leistung mit letzterem.
Kernbotschaften#
Kleine Unterschiede in den Leistungsmaßen können leicht zufällig sein und nicht darauf zurückzuführen sein, dass ein Modell systematisch besser vorhersagt als das andere. Wie in diesem Beispiel gezeigt, können Statistiken Ihnen sagen, wie wahrscheinlich das ist.
Beim statistischen Vergleich der Leistung zweier Modelle, die in GridSearchCV bewertet wurden, ist es notwendig, die berechnete Varianz zu korrigieren, die unterschätzt werden könnte, da die Scores der Modelle nicht voneinander unabhängig sind.
Ein frequentistischer Ansatz, der einen (variantenkorrigierten) gepaarten t-Test verwendet, kann uns mit einer über den Zufall hinausgehenden Wahrscheinlichkeit sagen, ob die Leistung eines Modells besser ist als die eines anderen.
Ein bayesianischer Ansatz kann die Wahrscheinlichkeiten liefern, dass ein Modell besser, schlechter oder praktisch äquivalent zu einem anderen ist. Er kann uns auch sagen, wie sicher wir uns sind, dass die wahren Unterschiede unserer Modelle in einen bestimmten Wertebereich fallen.
Wenn mehrere Modelle statistisch verglichen werden, ist eine Korrektur für Mehrfachvergleiche erforderlich, wenn der frequentistische Ansatz verwendet wird.
Referenzen
Gesamtlaufzeit des Skripts: (0 Minuten 1,443 Sekunden)
Verwandte Beispiele
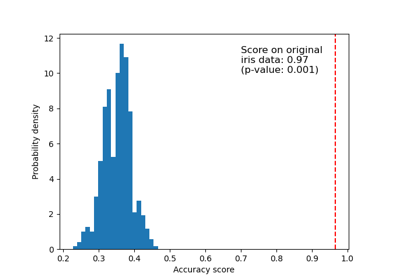
Testen der Signifikanz eines Klassifikations-Scores mit Permutationen
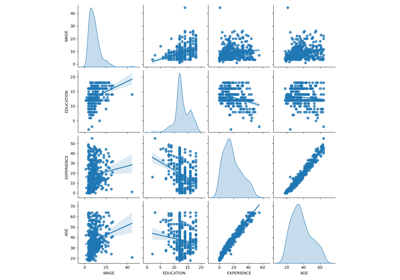
Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle

Beispiel-Pipeline für Textmerkmal-Extraktion und -Bewertung