Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Vorhersageintervalle für Gradient Boosting Regression#
Dieses Beispiel zeigt, wie Quantilregression zur Erstellung von Vorhersageintervallen verwendet werden kann. Weitere Beispiele für einige andere Funktionen von HistGradientBoostingRegressor finden Sie unter Funktionen in Histogramm-Gradient-Boosting-Bäumen.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Generieren Sie Daten für ein synthetisches Regressionsproblem, indem Sie die Funktion f auf gleichmäßig verteilte Zufallseingaben anwenden.
import numpy as np
from sklearn.model_selection import train_test_split
def f(x):
"""The function to predict."""
return x * np.sin(x)
rng = np.random.RandomState(42)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
Um das Problem interessant zu gestalten, generieren wir Beobachtungen des Ziels y als Summe eines deterministischen Terms, der von der Funktion f berechnet wird, und eines zufälligen Rauschterms, der einer zentrierten log-normalen Verteilung folgt. Um dies noch interessanter zu machen, betrachten wir den Fall, in dem die Amplitude des Rauschens von der Eingabevariable x abhängt (heteroskedastisches Rauschen).
Die Lognormalverteilung ist nicht symmetrisch und hat lange Ausläufer: Das Auftreten großer Ausreißer ist wahrscheinlich, aber das Auftreten kleiner Ausreißer ist unmöglich.
sigma = 0.5 + X.ravel() / 10
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2 / 2)
y = expected_y + noise
Aufteilung in Trainings-, Testdatensätze
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Anpassen von nicht-linearen Quantil- und Kleinstquadrate-Regressoren#
Passen Sie Gradient-Boosting-Modelle an, die mit dem Quantilverlust und alpha=0.05, 0.5, 0.95 trainiert wurden.
Die Modelle, die für alpha=0.05 und alpha=0.95 erzielt wurden, ergeben ein 90%iges Konfidenzintervall (95% - 5% = 90%).
Das mit alpha=0.5 trainierte Modell ergibt eine Regression des Medians: Im Durchschnitt sollte die gleiche Anzahl von Zielbeobachtungen über und unter den vorhergesagten Werten liegen.
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_pinball_loss, mean_squared_error
all_models = {}
common_params = dict(
learning_rate=0.05,
n_estimators=200,
max_depth=2,
min_samples_leaf=9,
min_samples_split=9,
)
for alpha in [0.05, 0.5, 0.95]:
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, **common_params)
all_models["q %1.2f" % alpha] = gbr.fit(X_train, y_train)
Beachten Sie, dass HistGradientBoostingRegressor ab mittleren Datensätzen (n_samples >= 10_000) deutlich schneller ist als GradientBoostingRegressor, was hier im Beispiel nicht der Fall ist.
Zum Vergleich passen wir auch ein Basislinienmodell an, das mit dem üblichen (mittleren) quadratischen Fehler (MSE) trainiert wurde.
gbr_ls = GradientBoostingRegressor(loss="squared_error", **common_params)
all_models["mse"] = gbr_ls.fit(X_train, y_train)
Erstellen Sie einen gleichmäßig beabstandeten Auswertungsdatensatz von Eingabewerten, die den Bereich [0, 10] abdecken.
xx = np.atleast_2d(np.linspace(0, 10, 1000)).T
Zeichnen Sie die wahre bedingte Mittelwertfunktion f, die Vorhersagen des bedingten Mittelwerts (Verlust gleich quadratischer Fehler), des bedingten Medians und des bedingten 90%-Intervalls (vom 5. bis zum 95. bedingten Perzentil).
import matplotlib.pyplot as plt
y_pred = all_models["mse"].predict(xx)
y_lower = all_models["q 0.05"].predict(xx)
y_upper = all_models["q 0.95"].predict(xx)
y_med = all_models["q 0.50"].predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.plot(xx, y_med, "tab:orange", linewidth=3, label="Predicted median")
plt.plot(xx, y_pred, "tab:green", linewidth=3, label="Predicted mean")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.show()
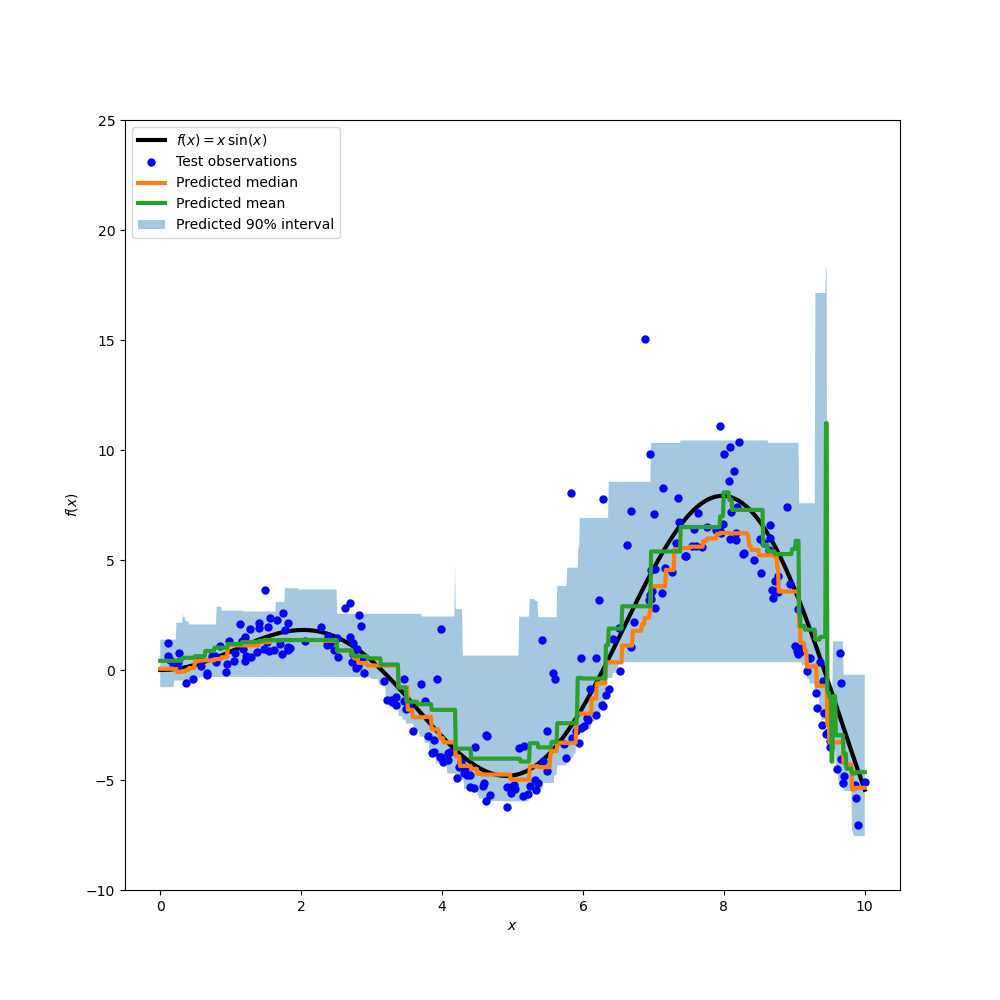
Vergleichen wir den vorhergesagten Median mit dem vorhergesagten Mittelwert. Wir stellen fest, dass der Median im Durchschnitt unter dem Mittelwert liegt, da das Rauschen zu hohen Werten hin verzerrt ist (große Ausreißer). Die Medianschätzung erscheint auch glatter, da sie von Natur aus robust gegenüber Ausreißern ist.
Beachten Sie auch, dass der induktive Bias von Gradient-Boosting-Bäumen leider verhindert, dass unser 0,05-Quantil die Sinusform des Signals vollständig erfasst, insbesondere um x=8. Die Abstimmung von Hyperparametern kann diesen Effekt reduzieren, wie im letzten Teil dieses Notebooks gezeigt wird.
Analyse der Fehlermetriken#
Messen Sie die Modelle mit den Metriken mean_squared_error und mean_pinball_loss auf dem Trainingsdatensatz.
import pandas as pd
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_train)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_train, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_train, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
Eine Spalte zeigt alle Modelle, die mit derselben Metrik bewertet wurden. Die Mindestanzahl in einer Spalte sollte erreicht werden, wenn das Modell mit derselben Metrik trainiert und gemessen wird. Dies sollte auf dem Trainingssatz immer der Fall sein, wenn das Training konvergiert ist.
Beachten Sie, dass aufgrund der asymmetrischen Zielverteilung der erwartete bedingte Mittelwert und der bedingte Median signifikant unterschiedlich sind und man daher das quadratische Fehlermodell nicht verwenden könnte, um eine gute Schätzung des bedingten Medians oder umgekehrt zu erhalten.
Wenn die Zielverteilung symmetrisch wäre und keine Ausreißer hätte (z. B. bei Gaußschem Rauschen), würden der Median-Schätzer und der Kleinstquadrate-Schätzer ähnliche Vorhersagen liefern.
Anschließend tun wir dasselbe auf dem Testdatensatz.
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_test)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_test, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_test, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
Die Fehler sind höher, was bedeutet, dass die Modelle die Daten leicht überangepasst haben. Es zeigt immer noch, dass die beste Testmetrik erzielt wird, wenn das Modell durch Minimierung derselben Metrik trainiert wird.
Beachten Sie, dass der bedingte Median-Schätzer in Bezug auf MSE auf dem Testdatensatz konkurrenzfähig mit dem quadratischen Fehler-Schätzer ist: Dies lässt sich dadurch erklären, dass der quadratische Fehler-Schätzer sehr empfindlich auf große Ausreißer reagiert, die zu erheblichen Überanpassungen führen können. Dies ist auf der rechten Seite der vorherigen Grafik zu sehen. Der bedingte Median-Schätzer ist verzerrt (bei diesem asymmetrischen Rauschen eine Unterabschätzung), aber von Natur aus robust gegenüber Ausreißern und überanpasst weniger.
Kalibrierung des Konfidenzintervalls#
Wir können auch die Fähigkeit der beiden extremen Quantil-Schätzer bewerten, ein gut kalibriertes bedingtes 90%-Konfidenzintervall zu erzeugen.
Dazu können wir den Anteil der Beobachtungen berechnen, die zwischen den Vorhersagen liegen
def coverage_fraction(y, y_low, y_high):
return np.mean(np.logical_and(y >= y_low, y <= y_high))
coverage_fraction(
y_train,
all_models["q 0.05"].predict(X_train),
all_models["q 0.95"].predict(X_train),
)
np.float64(0.9)
Auf dem Trainingsdatensatz ist die Kalibrierung der erwarteten Abdeckungsrate für ein 90%iges Konfidenzintervall sehr nahe.
coverage_fraction(
y_test, all_models["q 0.05"].predict(X_test), all_models["q 0.95"].predict(X_test)
)
np.float64(0.868)
Auf dem Testdatensatz ist das geschätzte Konfidenzintervall etwas zu schmal. Beachten Sie jedoch, dass wir diese Metriken in eine Kreuzvalidierungsschleife einpacken müssten, um ihre Variabilität unter Datenresampling zu bewerten.
Abstimmung der Hyperparameter der Quantilregressoren#
In der obigen Grafik beobachteten wir, dass der 5%-Perzentil-Regressor zu unterpassen scheint und sich nicht an die sinusförmige Form des Signals anpassen konnte.
Die Hyperparameter des Modells wurden für den Median-Regressor ungefähr von Hand abgestimmt, und es gibt keinen Grund anzunehmen, dass dieselben Hyperparameter für den 5%-Perzentil-Regressor geeignet sind.
Um diese Hypothese zu bestätigen, stimmen wir die Hyperparameter eines neuen Regressors für das 5. Perzentil ab, indem wir die besten Modellparameter mittels Kreuzvalidierung für den Pinball-Verlust mit alpha=0.05 auswählen.
from pprint import pprint
from sklearn.experimental import enable_halving_search_cv # noqa: F401
from sklearn.metrics import make_scorer
from sklearn.model_selection import HalvingRandomSearchCV
param_grid = dict(
learning_rate=[0.05, 0.1, 0.2],
max_depth=[2, 5, 10],
min_samples_leaf=[1, 5, 10, 20],
min_samples_split=[5, 10, 20, 30, 50],
)
alpha = 0.05
neg_mean_pinball_loss_05p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # maximize the negative loss
)
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, random_state=0)
search_05p = HalvingRandomSearchCV(
gbr,
param_grid,
resource="n_estimators",
max_resources=250,
min_resources=50,
scoring=neg_mean_pinball_loss_05p_scorer,
n_jobs=2,
random_state=0,
).fit(X_train, y_train)
pprint(search_05p.best_params_)
{'learning_rate': 0.2,
'max_depth': 2,
'min_samples_leaf': 20,
'min_samples_split': 10,
'n_estimators': 150}
Wir beobachten, dass die Hyperparameter, die für den Median-Regressor von Hand abgestimmt wurden, im selben Bereich liegen wie die für den 5%-Perzentil-Regressor geeigneten Hyperparameter.
Lassen Sie uns nun die Hyperparameter für den 95%-Perzentil-Regressor abstimmen. Wir müssen die scoring-Metrik neu definieren, die zur Auswahl des besten Modells verwendet wird, und gleichzeitig den Alpha-Parameter des inneren Gradient-Boosting-Schätzers selbst anpassen.
from sklearn.base import clone
alpha = 0.95
neg_mean_pinball_loss_95p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # maximize the negative loss
)
search_95p = clone(search_05p).set_params(
estimator__alpha=alpha,
scoring=neg_mean_pinball_loss_95p_scorer,
)
search_95p.fit(X_train, y_train)
pprint(search_95p.best_params_)
{'learning_rate': 0.05,
'max_depth': 2,
'min_samples_leaf': 5,
'min_samples_split': 20,
'n_estimators': 150}
Das Ergebnis zeigt, dass die Hyperparameter für den 95%-Perzentil-Regressor, die durch die Suchprozedur identifiziert wurden, ungefähr im selben Bereich liegen wie die von Hand abgestimmten Hyperparameter für den Median-Regressor und die durch die Suchprozedur für den 5%-Perzentil-Regressor identifizierten Hyperparameter. Die Hyperparameter-Suchen führten jedoch zu einem verbesserten 90%-Konfidenzintervall, das sich aus den Vorhersagen dieser beiden abgestimmten Quantilregressoren zusammensetzt. Beachten Sie, dass die Vorhersage des oberen 95. Perzentils aufgrund der Ausreißer eine deutlich gröbere Form hat als die Vorhersage des unteren 5. Perzentils.
y_lower = search_05p.predict(xx)
y_upper = search_95p.predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.title("Prediction with tuned hyper-parameters")
plt.show()
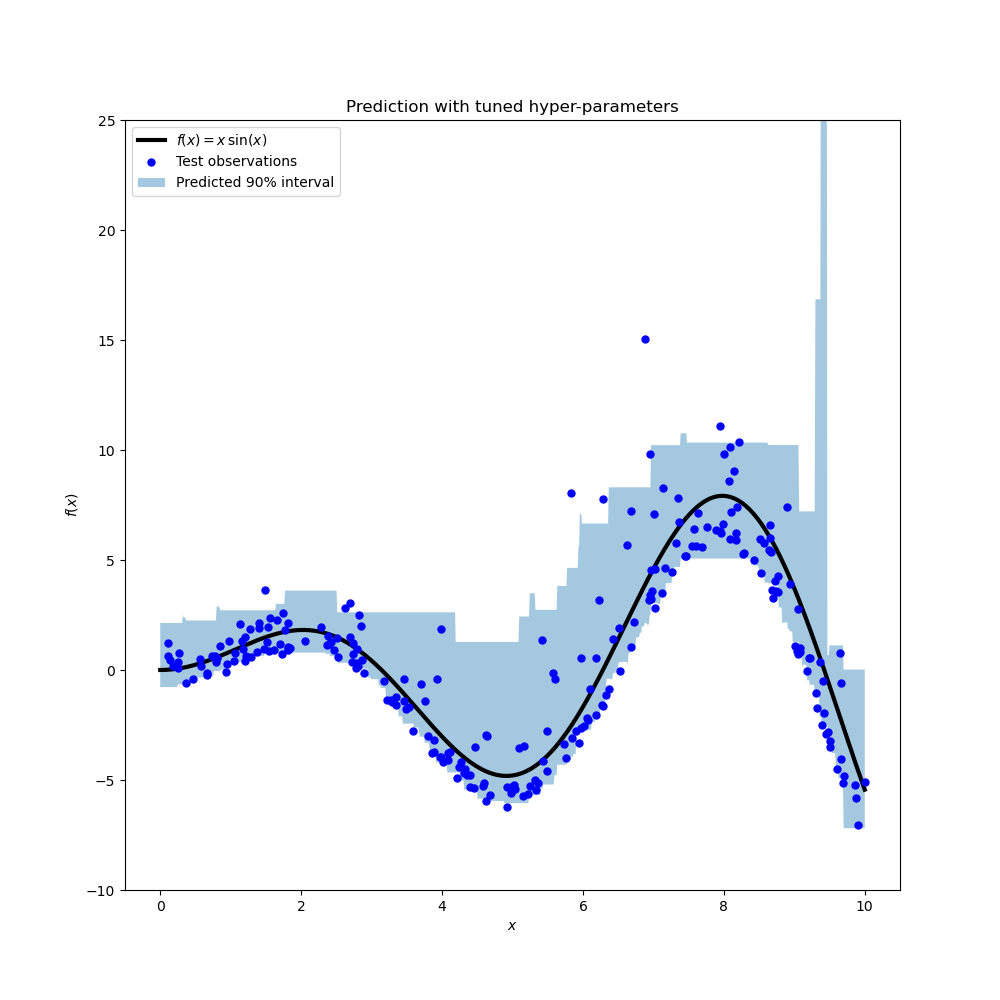
Die Grafik sieht qualitativ besser aus als bei den nicht abgestimmten Modellen, insbesondere was die Form des unteren Quantils betrifft.
Nun bewerten wir quantitativ die gemeinsame Kalibrierung des Schätzerpaares.
coverage_fraction(y_train, search_05p.predict(X_train), search_95p.predict(X_train))
np.float64(0.9026666666666666)
coverage_fraction(y_test, search_05p.predict(X_test), search_95p.predict(X_test))
np.float64(0.796)
Die Kalibrierung des abgestimmten Paares ist auf dem Testdatensatz leider nicht besser: Die Breite des geschätzten Konfidenzintervalls ist immer noch zu schmal.
Auch hier müssten wir diese Studie in eine Kreuzvalidierungsschleife einpacken, um die Variabilität dieser Schätzungen besser bewerten zu können.
Gesamtlaufzeit des Skripts: (0 Minuten 9,880 Sekunden)
Verwandte Beispiele
Gauß-Prozesse Regression: grundlegendes Einführungsexempel