Hinweis
Zum Ende gehen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel in Ihrem Browser über JupyterLite oder Binder auszuführen.
Entscheidungsbaum-Regression#
In diesem Beispiel demonstrieren wir den Effekt der Änderung der maximalen Tiefe eines Entscheidungsbaums auf dessen Anpassung an die Daten. Wir führen dies einmal für eine 1D-Regressionsaufgabe und einmal für eine Multi-Output-Regressionsaufgabe durch.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Entscheidungsbaum bei einer 1D-Regressionsaufgabe#
Hier passen wir einen Baum an eine 1D-Regressionsaufgabe an.
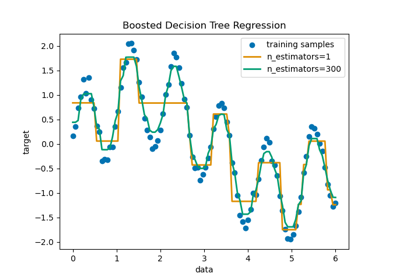
Der Entscheidungsbaum wird verwendet, um eine Sinuskurve mit zusätzlichen verrauschten Beobachtungen anzupassen. Als Ergebnis lernt er lokale lineare Regressionen, die die Sinuskurve approximieren.
Wir können sehen, dass, wenn die maximale Tiefe des Baums (gesteuert durch den Parameter max_depth) zu hoch eingestellt ist, die Entscheidungsbäume zu feine Details der Trainingsdaten lernen und aus dem Rauschen lernen, d.h. sie überanpassen.
Erstellen eines zufälligen 1D-Datensatzes#
import numpy as np
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
Regressionsmodell anpassen#
Hier passen wir zwei Modelle mit unterschiedlichen maximalen Tiefen an
from sklearn.tree import DecisionTreeRegressor
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
Vorhersage#
Vorhersagen auf dem Testdatensatz abrufen
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
Ergebnisse plotten#
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

Wie Sie sehen können, lernt das Modell mit einer Tiefe von 5 (gelb) die Details der Trainingsdaten bis zu dem Punkt, an dem es zu Rauschen überanpasst. Auf der anderen Seite lernt das Modell mit einer Tiefe von 2 (blau) die Haupttendenzen in den Daten gut und überpasst nicht. In realen Anwendungsfällen müssen Sie sicherstellen, dass der Baum die Trainingsdaten nicht überanpasst, was mit Kreuzvalidierung geschehen kann.
Entscheidungsbaum-Regression mit Multi-Output-Zielen#
Hier wird der Entscheidungsbaum verwendet, um gleichzeitig die verrauschten x- und y-Beobachtungen eines Kreises zu prognostizieren, gegeben ein einziges zugrunde liegendes Merkmal. Als Ergebnis lernt er lokale lineare Regressionen, die den Kreis approximieren.
Wir können sehen, dass, wenn die maximale Tiefe des Baums (gesteuert durch den Parameter max_depth) zu hoch eingestellt ist, die Entscheidungsbäume zu feine Details der Trainingsdaten lernen und aus dem Rauschen lernen, d.h. sie überanpassen.
Erstellen eines zufälligen Datensatzes#
Regressionsmodell anpassen#
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)
Vorhersage#
Vorhersagen auf dem Testdatensatz abrufen
X_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)
Ergebnisse plotten#
plt.figure()
s = 25
plt.scatter(y[:, 0], y[:, 1], c="yellow", s=s, edgecolor="black", label="data")
plt.scatter(
y_1[:, 0],
y_1[:, 1],
c="cornflowerblue",
s=s,
edgecolor="black",
label="max_depth=2",
)
plt.scatter(y_2[:, 0], y_2[:, 1], c="red", s=s, edgecolor="black", label="max_depth=5")
plt.scatter(y_3[:, 0], y_3[:, 1], c="blue", s=s, edgecolor="black", label="max_depth=8")
plt.xlim([-6, 6])
plt.ylim([-6, 6])
plt.xlabel("target 1")
plt.ylabel("target 2")
plt.title("Multi-output Decision Tree Regression")
plt.legend(loc="best")
plt.show()

Wie Sie sehen können, je höher der Wert von max_depth, desto mehr Details der Daten werden vom Modell erfasst. Allerdings überpasst das Modell auch die Daten und wird vom Rauschen beeinflusst.
Gesamtlaufzeit des Skripts: (0 Minuten 0,290 Sekunden)
Verwandte Beispiele
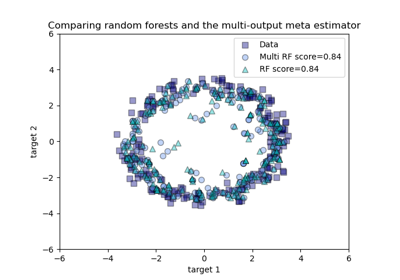
Vergleich von Random Forests und dem Multi-Output Meta-Estimator
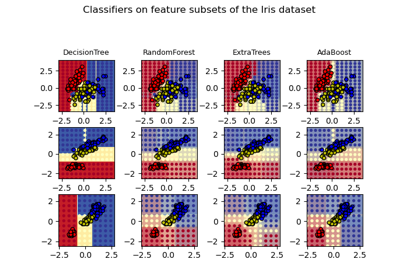
Entscheidungsflächen von Ensembles von Bäumen auf dem Iris-Datensatz plotten