Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder im Browser auszuführen.
Manifold Learning auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap…
Wir illustrieren verschiedene Embedding-Techniken am Datensatz der Ziffern.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Laden des Datensatzes der Ziffern
Wir laden den Datensatz der Ziffern und verwenden nur die ersten sechs der zehn verfügbaren Klassen.
from sklearn.datasets import load_digits
digits = load_digits(n_class=6)
X, y = digits.data, digits.target
n_samples, n_features = X.shape
n_neighbors = 30
Wir können die ersten hundert Ziffern aus diesem Datensatz plotten.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
ax.imshow(X[idx].reshape((8, 8)), cmap=plt.cm.binary)
ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)

Hilfsfunktion zum Plotten des Embeddings
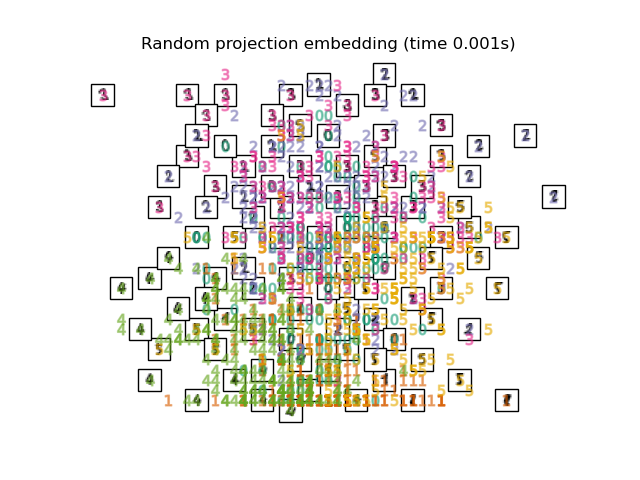
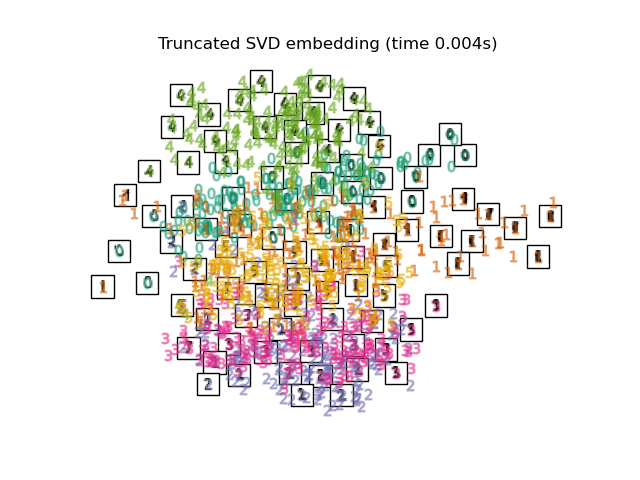
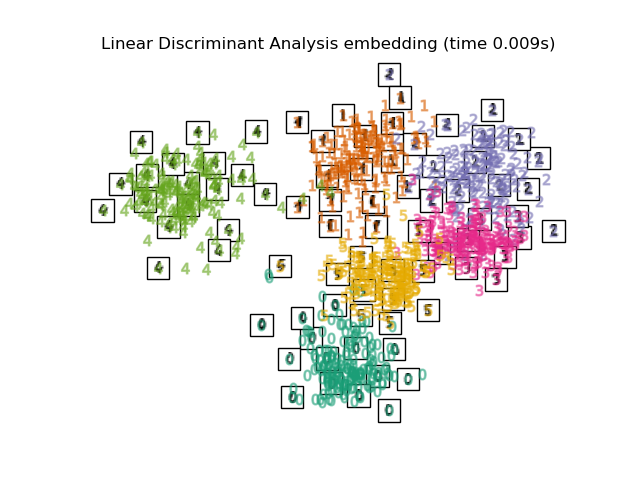
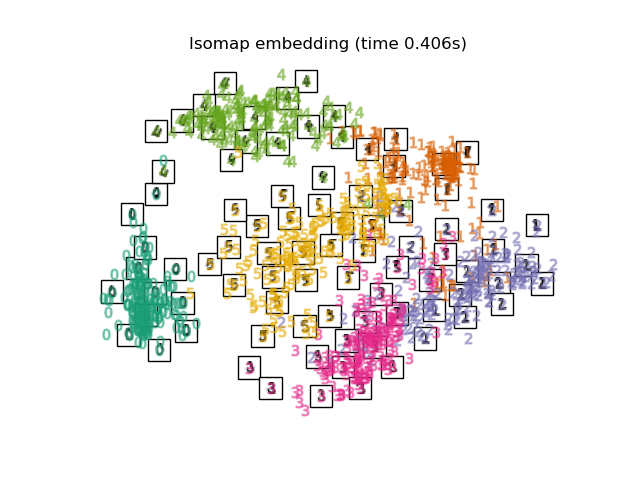
Unten werden wir verschiedene Techniken verwenden, um den Datensatz der Ziffern einzubetten. Wir werden die Projektion der Originaldaten auf jedes Embedding plotten. Dies wird es uns ermöglichen zu überprüfen, ob die Ziffern im Embedding-Raum zusammen gruppiert sind oder über ihn verstreut sind.
import numpy as np
from matplotlib import offsetbox
from sklearn.preprocessing import MinMaxScaler
def plot_embedding(X, title):
_, ax = plt.subplots()
X = MinMaxScaler().fit_transform(X)
for digit in digits.target_names:
ax.scatter(
*X[y == digit].T,
marker=f"${digit}$",
s=60,
color=plt.cm.Dark2(digit),
alpha=0.425,
zorder=2,
)
shown_images = np.array([[1.0, 1.0]]) # just something big
for i in range(X.shape[0]):
# plot every digit on the embedding
# show an annotation box for a group of digits
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = np.concatenate([shown_images, [X[i]]], axis=0)
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r), X[i]
)
imagebox.set(zorder=1)
ax.add_artist(imagebox)
ax.set_title(title)
ax.axis("off")
Vergleich von Embedding-Techniken
Unten vergleichen wir verschiedene Techniken. Es gibt jedoch ein paar Dinge zu beachten:
das
RandomTreesEmbeddingist technisch gesehen keine Manifold-Embedding-Methode, da es eine hochdimensionale Darstellung lernt, auf die wir eine Dimensionsreduktionsmethode anwenden. Es ist jedoch oft nützlich, einen Datensatz in eine Darstellung zu überführen, in der die Klassen linear trennbar sind.die
LinearDiscriminantAnalysisund dieNeighborhoodComponentsAnalysissind überwachte Dimensionsreduktionsmethoden, d. h. sie nutzen die bereitgestellten Labels, im Gegensatz zu anderen Methoden.das
TSNEwird in diesem Beispiel mit dem durch PCA erzeugten Embedding initialisiert. Dies gewährleistet die globale Stabilität des Embeddings, d. h. das Embedding hängt nicht von der zufälligen Initialisierung ab.
from sklearn.decomposition import TruncatedSVD
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.ensemble import RandomTreesEmbedding
from sklearn.manifold import (
MDS,
TSNE,
ClassicalMDS,
Isomap,
LocallyLinearEmbedding,
SpectralEmbedding,
)
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.random_projection import SparseRandomProjection
embeddings = {
"Random projection embedding": SparseRandomProjection(
n_components=2, random_state=42
),
"Truncated SVD embedding": TruncatedSVD(n_components=2),
"Linear Discriminant Analysis embedding": LinearDiscriminantAnalysis(
n_components=2
),
"Isomap embedding": Isomap(n_neighbors=n_neighbors, n_components=2),
"Standard LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="standard"
),
"Modified LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="modified"
),
"Hessian LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="hessian"
),
"LTSA LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="ltsa"
),
"Metric MDS embedding": MDS(n_components=2, n_init=1, init="classical_mds"),
"Non-metric MDS embedding": MDS(
n_components=2, n_init=1, init="classical_mds", metric_mds=False
),
"Classical MDS embedding": ClassicalMDS(n_components=2),
"Random Trees embedding": make_pipeline(
RandomTreesEmbedding(n_estimators=200, max_depth=5, random_state=0),
TruncatedSVD(n_components=2),
),
"Spectral embedding": SpectralEmbedding(
n_components=2, random_state=0, eigen_solver="arpack"
),
"t-SNE embedding": TSNE(
n_components=2,
max_iter=500,
n_iter_without_progress=150,
n_jobs=2,
random_state=0,
),
"NCA embedding": NeighborhoodComponentsAnalysis(
n_components=2, init="pca", random_state=0
),
}
Nachdem wir alle interessierenden Methoden deklariert haben, können wir die Projektion der Originaldaten ausführen und durchführen. Wir speichern die projizierten Daten sowie die benötigte Rechenzeit für jede Projektion.
from time import time
projections, timing = {}, {}
for name, transformer in embeddings.items():
if name.startswith("Linear Discriminant Analysis"):
data = X.copy()
data.flat[:: X.shape[1] + 1] += 0.01 # Make X invertible
else:
data = X
print(f"Computing {name}...")
start_time = time()
projections[name] = transformer.fit_transform(data, y)
timing[name] = time() - start_time
Computing Random projection embedding...
Computing Truncated SVD embedding...
Computing Linear Discriminant Analysis embedding...
Computing Isomap embedding...
Computing Standard LLE embedding...
Computing Modified LLE embedding...
Computing Hessian LLE embedding...
Computing LTSA LLE embedding...
Computing Metric MDS embedding...
Computing Non-metric MDS embedding...
Computing Classical MDS embedding...
Computing Random Trees embedding...
Computing Spectral embedding...
Computing t-SNE embedding...
Computing NCA embedding...
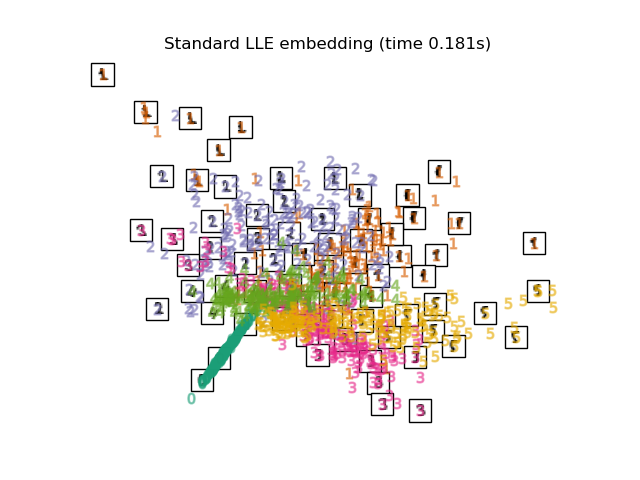
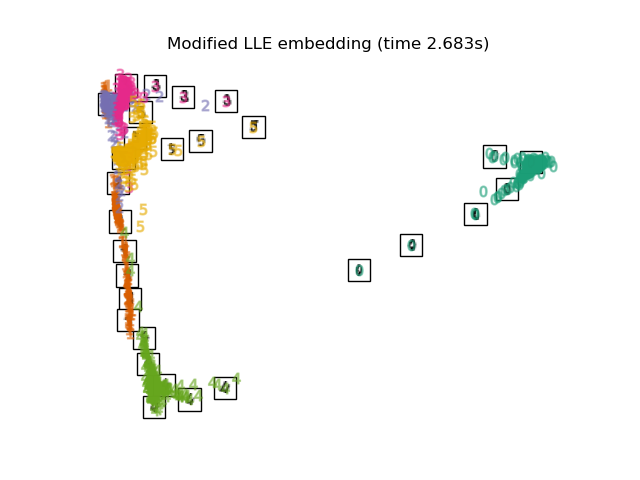
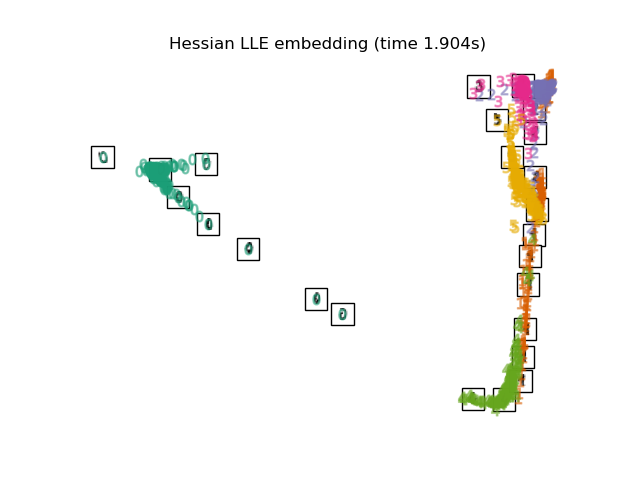
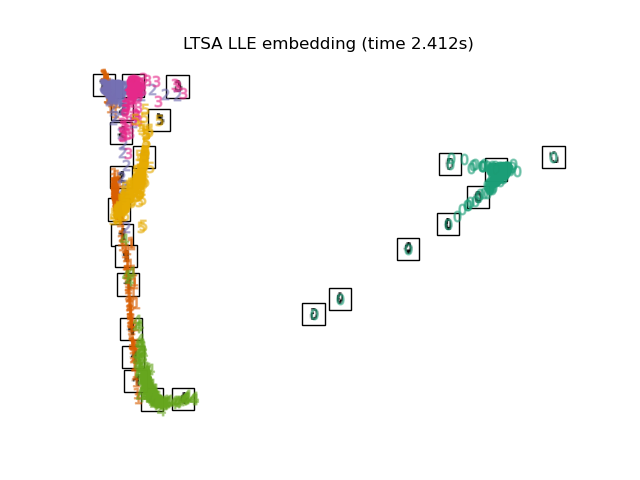
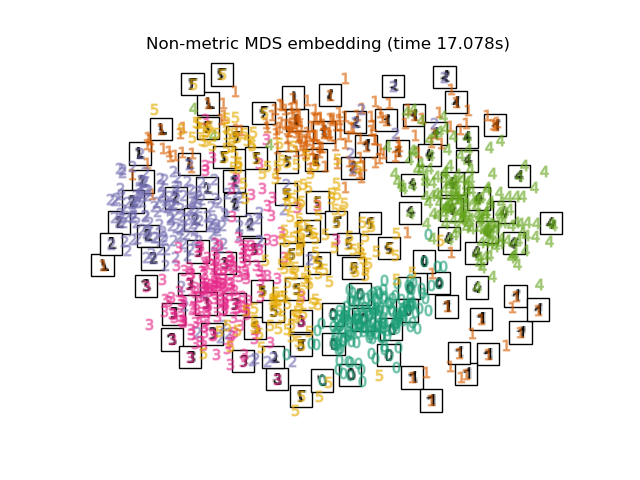
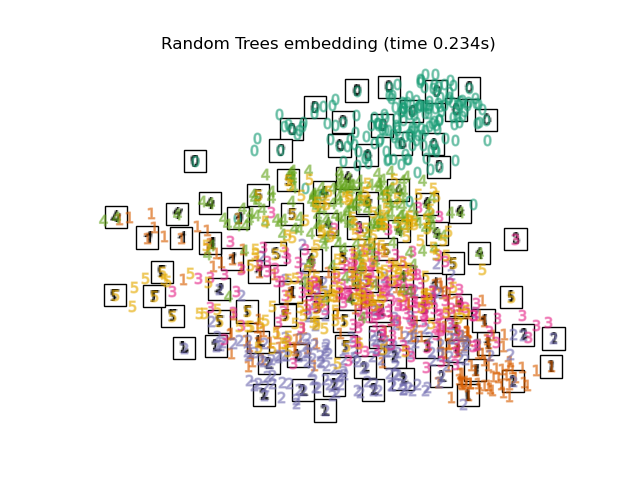
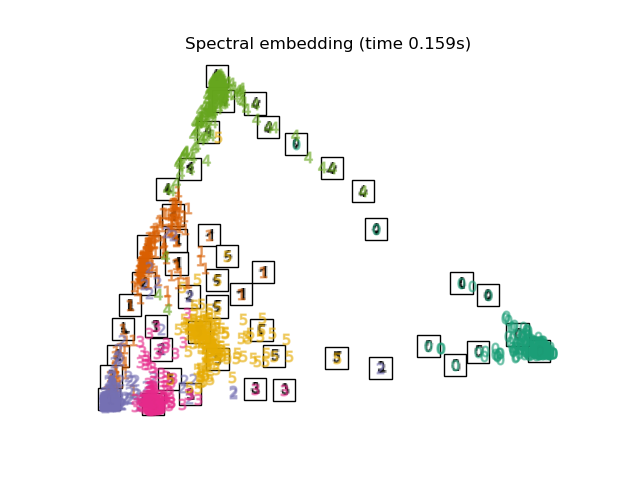
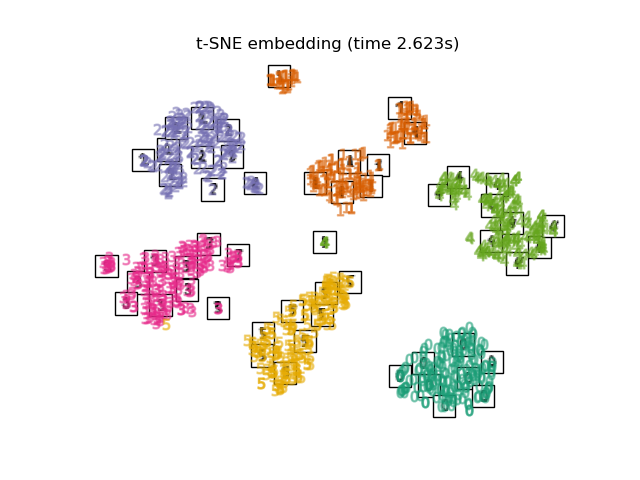
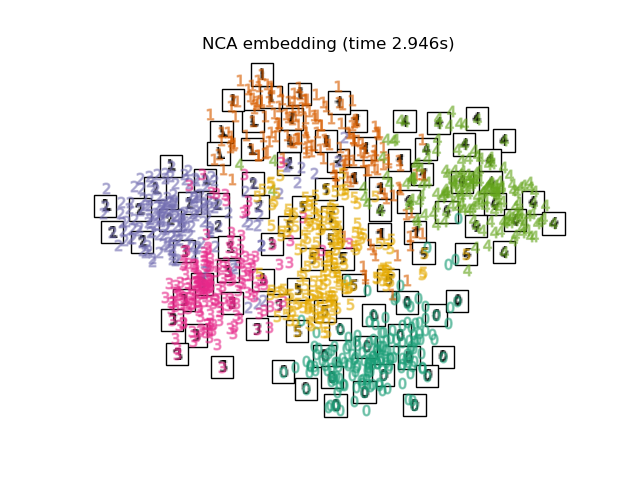
Schließlich können wir die von jeder Methode gelieferte Ergebnisprojektion plotten.
for name in timing:
title = f"{name} (time {timing[name]:.3f}s)"
plot_embedding(projections[name], title)
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 37,999 Sekunden)
Verwandte Beispiele
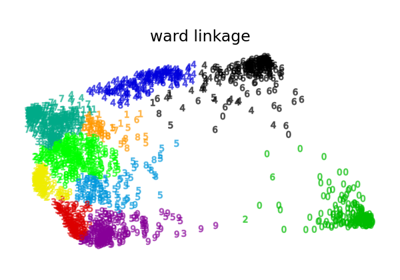
Verschiedenes Agglomeratives Clustering auf einer 2D-Einbettung von Ziffern