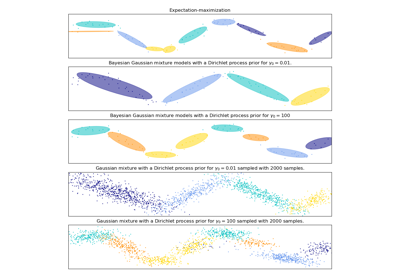
Gaußsche Mischungsmodell-Ellipsen

Zeichnen der Konfidenzellipsen einer Mischung aus zwei Gaußschen Verteilungen, die mit Erwartungsmaximierung (GaussianMixture Klasse) und Variationsinferenz (BayesianGaussianMixture Klasse mit einem Dirichlet-Prozess-Prior) erhalten wurden.

Beide Modelle haben Zugriff auf fünf Komponenten, um die Daten anzupassen. Beachten Sie, dass das Erwartungsmaximierungsmodell zwangsläufig alle fünf Komponenten verwendet, während das Variationsinferenzmodell effektiv nur so viele verwendet, wie für eine gute Anpassung benötigt werden. Hier sehen wir, dass das Erwartungsmaximierungsmodell einige Komponenten willkürlich aufteilt, da es versucht, zu viele Komponenten anzupassen, während das Dirichlet-Prozess-Modell seine Anzahl an Zuständen automatisch anpasst.

Dieses Beispiel zeigt es nicht, da wir uns in einem niedrigdimensionalen Raum befinden, aber ein weiterer Vorteil des Dirichlet-Prozess-Modells ist, dass es volle Kovarianzmatrizen effektiv anpassen kann, selbst wenn es weniger Beispiele pro Cluster als Dimensionen in den Daten gibt, aufgrund der Regularisierungseigenschaften des Inferenzalgorithmus.

/home/circleci/project/sklearn/mixture/_base.py:293: ConvergenceWarning:

Best performing initialization did not converge. Try different init parameters, or increase max_iter, tol, or check for degenerate data.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import itertools

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg

from sklearn import mixture

color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])


def plot_results(X, Y_, means, covariances, index, title):
    splot = plt.subplot(2, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y_ == i):
            continue
        plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180.0 * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-9.0, 5.0)
    plt.ylim(-3.0, 6.0)
    plt.xticks(())
    plt.yticks(())
    plt.title(title)


# Number of samples per component
n_samples = 500

# Generate random sample, two components
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
X = np.r_[
    np.dot(np.random.randn(n_samples, 2), C),
    0.7 * np.random.randn(n_samples, 2) + np.array([-6, 3]),
]

# Fit a Gaussian mixture with EM using five components
gmm = mixture.GaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Gaussian Mixture")

# Fit a Dirichlet process Gaussian mixture using five components
dpgmm = mixture.BayesianGaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    1,
    "Bayesian Gaussian Mixture with a Dirichlet process prior",
)

plt.show()

Verwandte Beispiele

Gaußsche Mischmodell-Sinuskurve

Gaußsche Mischmodell-Sinuskurve

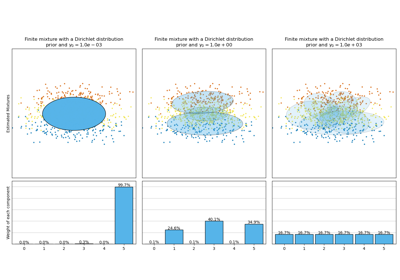
Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch

Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch

GMM Kovarianzen

GMM Kovarianzen

Gaußsche Mischmodell-Auswahl

Gaußsche Mischmodell-Auswahl