Kompressionssensorik: Tomographie-Rekonstruktion mit L1-Prior (Lasso)

Dieses Beispiel zeigt die Rekonstruktion eines Bildes aus einer Menge paralleler Projektionen, die unter verschiedenen Winkeln erfasst wurden. Ein solches Datenset wird in der Computertomographie (CT) erfasst.

Ohne Vorabinformationen über die Probe ist die Anzahl der Projektionen, die zur Rekonstruktion des Bildes benötigt werden, von der Größenordnung der linearen Größe l des Bildes (in Pixeln). Vereinfacht gesagt, betrachten wir hier ein dünnbesetztes Bild, bei dem nur Pixel am Rand von Objekten einen von Null verschiedenen Wert haben. Solche Daten könnten beispielsweise ein zelluläres Material darstellen. Beachten Sie jedoch, dass die meisten Bilder in einer anderen Basis, wie z. B. Haar-Wavelets, dünnbesetzt sind. Es werden nur l/7 Projektionen erfasst, daher ist es notwendig, Vorabinformationen über die Probe (ihre Dünnbesetztheit) zu verwenden: Dies ist ein Beispiel für Kompressionssensorik.

Die Tomographie-Projektionsoperation ist eine lineare Transformation. Zusätzlich zum Daten-Treue-Term, der einer linearen Regression entspricht, bestrafen wir die L1-Norm des Bildes, um seine Dünnbesetztheit zu berücksichtigen. Das resultierende Optimierungsproblem wird als Lasso bezeichnet. Wir verwenden die Klasse Lasso, die den Koordinatenabstieg-Algorithmus verwendet. Wichtig ist, dass diese Implementierung auf einer dünnbesetzten Matrix rechnerisch effizienter ist als der hier verwendete Projektionsoperator.

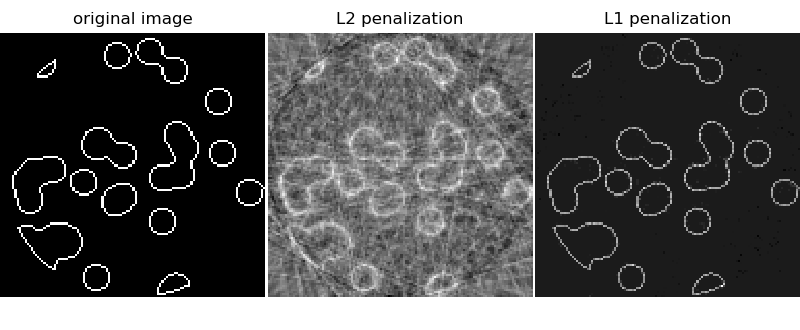
Die Rekonstruktion mit L1-Regularisierung ergibt ein Ergebnis mit Null Fehlern (alle Pixel werden erfolgreich mit 0 oder 1 gekennzeichnet), selbst wenn Rauschen zu den Projektionen hinzugefügt wurde. Im Vergleich dazu erzeugt eine L2-Regularisierung (Ridge) eine große Anzahl von Kennzeichnungsfehlern für die Pixel. Wichtige Artefakte sind auf dem rekonstruierten Bild zu beobachten, im Gegensatz zur L1-Regularisierung. Beachten Sie insbesondere das kreisförmige Artefakt, das die Pixel in den Ecken trennt, die zu weniger Projektionen beigetragen haben als die zentrale Scheibe.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from scipy import ndimage, sparse

from sklearn.linear_model import Lasso, Ridge


def _weights(x, dx=1, orig=0):
    x = np.ravel(x)
    floor_x = np.floor((x - orig) / dx).astype(np.int64)
    alpha = (x - orig - floor_x * dx) / dx
    return np.hstack((floor_x, floor_x + 1)), np.hstack((1 - alpha, alpha))


def _generate_center_coordinates(l_x):
    X, Y = np.mgrid[:l_x, :l_x].astype(np.float64)
    center = l_x / 2.0
    X += 0.5 - center
    Y += 0.5 - center
    return X, Y


def build_projection_operator(l_x, n_dir):
    """Compute the tomography design matrix.

    Parameters
    ----------

    l_x : int
        linear size of image array

    n_dir : int
        number of angles at which projections are acquired.

    Returns
    -------
    p : sparse matrix of shape (n_dir l_x, l_x**2)
    """
    X, Y = _generate_center_coordinates(l_x)
    angles = np.linspace(0, np.pi, n_dir, endpoint=False)
    data_inds, weights, camera_inds = [], [], []
    data_unravel_indices = np.arange(l_x**2)
    data_unravel_indices = np.hstack((data_unravel_indices, data_unravel_indices))
    for i, angle in enumerate(angles):
        Xrot = np.cos(angle) * X - np.sin(angle) * Y
        inds, w = _weights(Xrot, dx=1, orig=X.min())
        mask = np.logical_and(inds >= 0, inds < l_x)
        weights += list(w[mask])
        camera_inds += list(inds[mask] + i * l_x)
        data_inds += list(data_unravel_indices[mask])
    proj_operator = sparse.coo_matrix((weights, (camera_inds, data_inds)))
    return proj_operator


def generate_synthetic_data():
    """Synthetic binary data"""
    rs = np.random.RandomState(0)
    n_pts = 36
    x, y = np.ogrid[0:l, 0:l]
    mask_outer = (x - l / 2.0) ** 2 + (y - l / 2.0) ** 2 < (l / 2.0) ** 2
    mask = np.zeros((l, l))
    points = l * rs.rand(2, n_pts)
    mask[(points[0]).astype(int), (points[1]).astype(int)] = 1
    mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
    res = np.logical_and(mask > mask.mean(), mask_outer)
    return np.logical_xor(res, ndimage.binary_erosion(res))


# Generate synthetic images, and projections
l = 128
proj_operator = build_projection_operator(l, l // 7)
data = generate_synthetic_data()
proj = proj_operator @ data.ravel()[:, np.newaxis]
proj += 0.15 * np.random.randn(*proj.shape)

# Reconstruction with L2 (Ridge) penalization
rgr_ridge = Ridge(alpha=0.2)
rgr_ridge.fit(proj_operator, proj.ravel())
rec_l2 = rgr_ridge.coef_.reshape(l, l)

# Reconstruction with L1 (Lasso) penalization
# the best value of alpha was determined using cross validation
# with LassoCV
rgr_lasso = Lasso(alpha=0.001)
rgr_lasso.fit(proj_operator, proj.ravel())
rec_l1 = rgr_lasso.coef_.reshape(l, l)

plt.figure(figsize=(8, 3.3))
plt.subplot(131)
plt.imshow(data, cmap=plt.cm.gray, interpolation="nearest")
plt.axis("off")
plt.title("original image")
plt.subplot(132)
plt.imshow(rec_l2, cmap=plt.cm.gray, interpolation="nearest")
plt.title("L2 penalization")
plt.axis("off")
plt.subplot(133)
plt.imshow(rec_l1, cmap=plt.cm.gray, interpolation="nearest")
plt.title("L1 penalization")
plt.axis("off")

plt.subplots_adjust(hspace=0.01, wspace=0.01, top=1, bottom=0, left=0, right=1)

plt.show()

Verwandte Beispiele

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Spektrales Clustering für Bildsegmentierung

Spektrales Clustering für Bildsegmentierung

L1-basierte Modelle für sparse Signale

L1-basierte Modelle für sparse Signale

Lasso auf dichten und spärlichen Daten

Lasso auf dichten und spärlichen Daten