Isotonische Regression

Eine Veranschaulichung der isotonischen Regression an generierten Daten (nicht-linearer monotoner Trend mit homoskedastischem uniformem Rauschen).

Der Algorithmus der isotonischen Regression findet eine nicht abnehmende Annäherung einer Funktion, während er den mittleren quadratischen Fehler auf den Trainingsdaten minimiert. Der Vorteil eines solchen nicht-parametrischen Modells ist, dass es neben der Monotonie keine Form für die Zielfunktion annimmt. Zum Vergleich wird auch eine lineare Regression dargestellt.

Die Abbildung auf der rechten Seite zeigt die Modellvorhersagefunktion, die sich aus der linearen Interpolation von Schwellenpunkten ergibt. Die Schwellenpunkte sind eine Teilmenge der beobachteten Eingangsdaten des Trainingsdatensatzes und ihre entsprechenden Zielwerte werden durch die nicht-parametrische isotonische Anpassung berechnet.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import LineCollection

from sklearn.isotonic import IsotonicRegression
from sklearn.linear_model import LinearRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50.0 * np.log1p(np.arange(n))

Fit IsotonicRegression und LinearRegression Modelle

ir = IsotonicRegression(out_of_bounds="clip")
y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  # x needs to be 2d for LinearRegression

LinearRegression()

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Ergebnisse plotten

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 6))

ax0.plot(x, y, "C0.", markersize=12)
ax0.plot(x, y_, "C1.-", markersize=12)
ax0.plot(x, lr.predict(x[:, np.newaxis]), "C2-")
ax0.add_collection(lc)
ax0.legend(("Training data", "Isotonic fit", "Linear fit"), loc="lower right")
ax0.set_title("Isotonic regression fit on noisy data (n=%d)" % n)

x_test = np.linspace(-10, 110, 1000)
ax1.plot(x_test, ir.predict(x_test), "C1-")
ax1.plot(ir.X_thresholds_, ir.y_thresholds_, "C1.", markersize=12)
ax1.set_title("Prediction function (%d thresholds)" % len(ir.X_thresholds_))

plt.show()

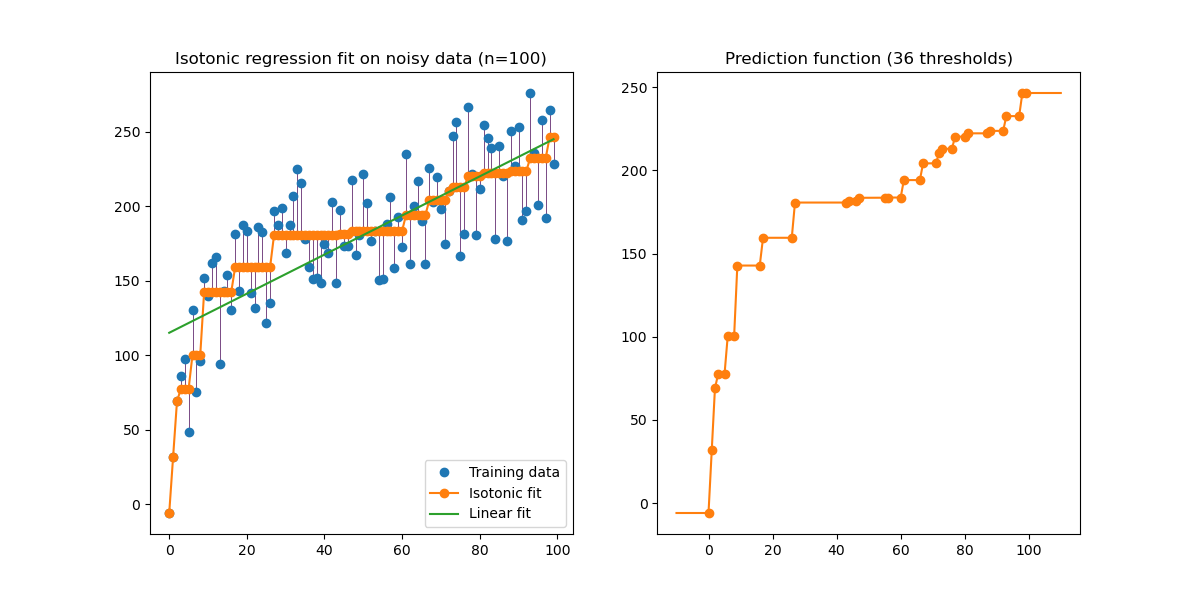
Beachten Sie, dass wir explizit out_of_bounds="clip" an den Konstruktor von IsotonicRegression übergeben haben, um die Art und Weise zu steuern, wie das Modell außerhalb des im Trainingsdatensatz beobachteten Datenbereichs extrapoliert. Diese "Clipping"-Extrapolation ist in der Abbildung der Entscheidungsfunktion auf der rechten Seite zu sehen.

Verwandte Beispiele

Auswirkung der Transformation der Ziele in einem Regressionsmodell

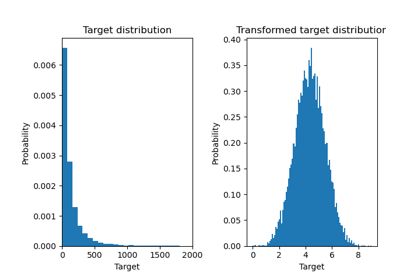
Auswirkung der Transformation der Ziele in einem Regressionsmodell

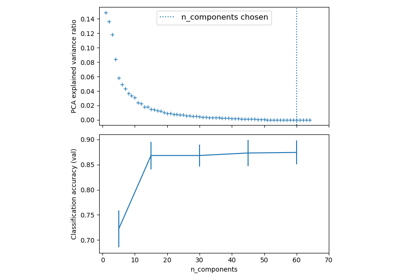
Pipelining: Verkettung einer PCA und einer logistischen Regression

Pipelining: Verkettung einer PCA und einer logistischen Regression

Wahrscheinlichkeitskalibrierungskurven

Wahrscheinlichkeitskalibrierungskurven

Wahrscheinlichkeitskalibrierung von Klassifikatoren

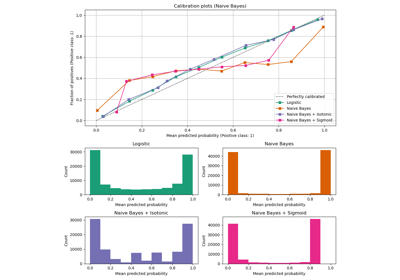
Wahrscheinlichkeitskalibrierung von Klassifikatoren