Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
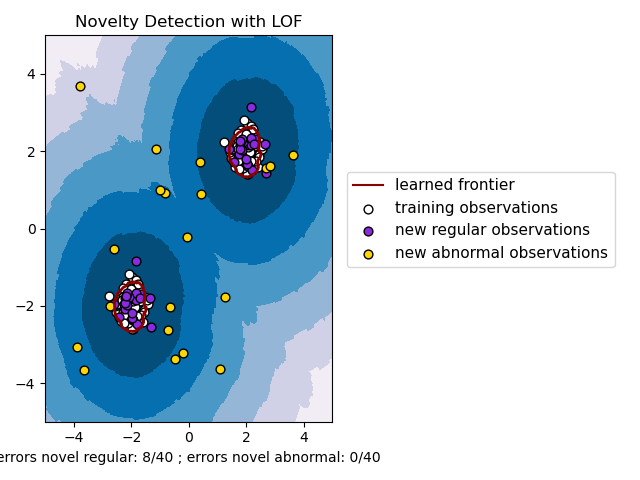
Neuheitserkennung mit Local Outlier Factor (LOF)#
Der Algorithmus Local Outlier Factor (LOF) ist eine unüberwachte Methode zur Anomalieerkennung, die die lokale Dichtungsabweichung eines gegebenen Datenpunkts im Verhältnis zu seinen Nachbarn berechnet. Er betrachtet Stichproben mit einer erheblich geringeren Dichte als ihre Nachbarn als Ausreißer. Dieses Beispiel zeigt, wie LOF zur Neuheitserkennung verwendet wird. Beachten Sie, dass Sie bei der Verwendung von LOF zur Neuheitserkennung NICHT predict, decision_function und score_samples auf dem Trainingsdatensatz verwenden DÜRFEN, da dies zu falschen Ergebnissen führen würde. Sie dürfen diese Methoden nur auf neue, ungesehene Daten anwenden (die nicht im Trainingsdatensatz enthalten sind). Siehe Benutzerhandbuch: für Details zum Unterschied zwischen Ausreißererkennung und Neuheitserkennung und wie LOF zur Ausreißererkennung verwendet wird.
Die Anzahl der betrachteten Nachbarn (Parameter n_neighbors) wird typischerweise so gesetzt, dass sie 1) größer ist als die Mindestanzahl von Stichproben, die ein Cluster enthalten muss, damit andere Stichproben relativ zu diesem Cluster lokale Ausreißer sein können, und 2) kleiner ist als die maximale Anzahl von nahe gelegenen Stichproben, die potenziell lokale Ausreißer sein können. In der Praxis sind solche Informationen im Allgemeinen nicht verfügbar, und die Einstellung von n_neighbors=20 scheint im Allgemeinen gut zu funktionieren.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
import numpy as np
from sklearn.neighbors import LocalOutlierFactor
np.random.seed(42)
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# Generate normal (not abnormal) training observations
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# Generate new normal (not abnormal) observations
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
# fit the model for novelty detection (novelty=True)
clf = LocalOutlierFactor(n_neighbors=20, novelty=True, contamination=0.1)
clf.fit(X_train)
# DO NOT use predict, decision_function and score_samples on X_train as this
# would give wrong results but only on new unseen data (not used in X_train),
# e.g. X_test, X_outliers or the meshgrid
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size
# plot the learned frontier, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("Novelty Detection with LOF")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="darkred")
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors="palevioletred")
s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c="white", s=s, edgecolors="k")
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c="blueviolet", s=s, edgecolors="k")
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c="gold", s=s, edgecolors="k")
plt.axis("tight")
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend(
[mlines.Line2D([], [], color="darkred"), b1, b2, c],
[
"learned frontier",
"training observations",
"new regular observations",
"new abnormal observations",
],
loc=(1.05, 0.4),
prop=matplotlib.font_manager.FontProperties(size=11),
)
plt.xlabel(
"errors novel regular: %d/40 ; errors novel abnormal: %d/40"
% (n_error_test, n_error_outliers)
)
plt.tight_layout()
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,705 Sekunden)
Verwandte Beispiele
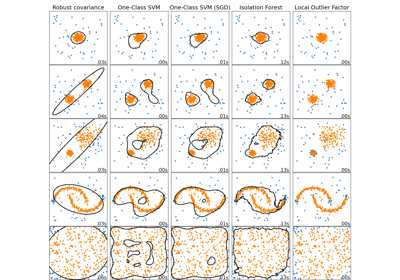
Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen
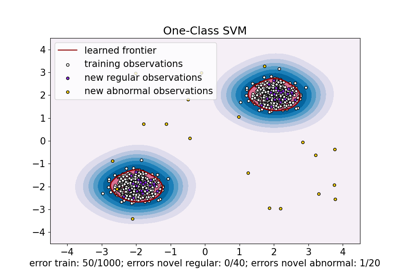
One-Class SVM vs. One-Class SVM mittels Stochastic Gradient Descent