Theil-Sen Regression

Berechnet eine Theil-Sen-Regression auf einem synthetischen Datensatz.

Weitere Informationen zum Regressor finden Sie unter Theil-Sen-Schätzer: verallgemeinerter medianbasierter Schätzer.

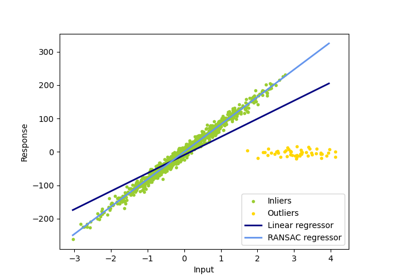
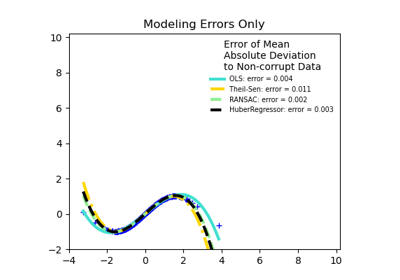
Im Vergleich zum OLS-Schätzer (Ordinary Least Squares) ist der Theil-Sen-Schätzer robust gegenüber Ausreißern. Er hat einen Bruchpunkt von etwa 29,3 % bei einer einfachen linearen Regression, was bedeutet, dass er bis zu 29,3 % beliebig korrupte Daten (Ausreißer) im zweidimensionalen Fall tolerieren kann.

Die Schätzung des Modells erfolgt durch Berechnung der Steigungen und Achsenabschnitte einer Teilpopulation aller möglichen Kombinationen von p Teil-Stichprobenpunkten. Wenn ein Achsenabschnitt angepasst wird, muss p größer oder gleich n_features + 1 sein. Die endgültige Steigung und der Achsenabschnitt werden dann als räumlicher Median dieser Steigungen und Achsenabschnitte definiert.

In bestimmten Fällen schneidet Theil-Sen besser ab als RANSAC, was ebenfalls eine robuste Methode ist. Dies wird im zweiten Beispiel unten veranschaulicht, wo Ausreißer in Bezug auf die x-Achse RANSAC stören. Das Anpassen des Parameters residual_threshold von RANSAC behebt dies, aber im Allgemeinen ist Vorwissen über die Daten und die Art der Ausreißer erforderlich. Aufgrund der Rechenkomplexität von Theil-Sen wird empfohlen, ihn nur für kleine Probleme in Bezug auf die Anzahl der Stichproben und Merkmale zu verwenden. Für größere Probleme schränkt der Parameter max_subpopulation die Größe aller möglichen Kombinationen von p Teil-Stichprobenpunkten auf eine zufällig ausgewählte Teilmenge ein und begrenzt somit auch die Laufzeit. Daher ist Theil-Sen für größere Probleme anwendbar, mit dem Nachteil, einige seiner mathematischen Eigenschaften zu verlieren, da er dann auf einer zufälligen Teilmenge arbeitet.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression, RANSACRegressor, TheilSenRegressor

estimators = [
    ("OLS", LinearRegression()),
    ("Theil-Sen", TheilSenRegressor(random_state=42)),
    ("RANSAC", RANSACRegressor(random_state=42)),
]
colors = {"OLS": "turquoise", "Theil-Sen": "gold", "RANSAC": "lightgreen"}
lw = 2

Nur Ausreißer in y-Richtung

np.random.seed(0)
n_samples = 200
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
w = 3.0
c = 2.0
noise = 0.1 * np.random.randn(n_samples)
y = w * x + c + noise
# 10% outliers
y[-20:] += -20 * x[-20:]
X = x[:, np.newaxis]

plt.scatter(x, y, color="indigo", marker="x", s=40)
line_x = np.array([-3, 3])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper right")
_ = plt.title("Corrupt y")

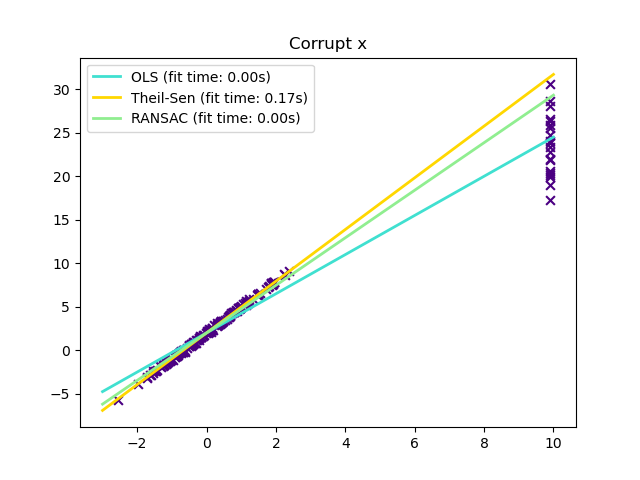
Ausreißer in x-Richtung

np.random.seed(0)
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
noise = 0.1 * np.random.randn(n_samples)
y = 3 * x + 2 + noise
# 10% outliers
x[-20:] = 9.9
y[-20:] += 22
X = x[:, np.newaxis]

plt.figure()
plt.scatter(x, y, color="indigo", marker="x", s=40)

line_x = np.array([-3, 10])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
plt.title("Corrupt x")
plt.show()

Verwandte Beispiele

Robuste lineare Modellschätzung mit RANSAC

Robuste lineare Modellschätzung mit RANSAC

Robuste lineare Schätzeranpassung

Robuste lineare Schätzeranpassung

Vergleich der Auswirkungen verschiedener Skalierer auf Daten mit Ausreißern

Vergleich der Auswirkungen verschiedener Skalierer auf Daten mit Ausreißern

Gewöhnliche kleinste Quadrate und Ridge Regression

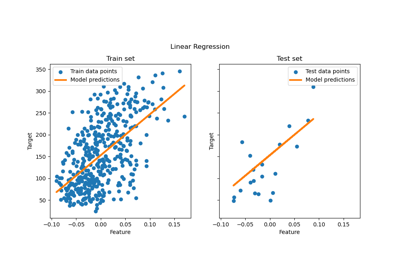
Gewöhnliche kleinste Quadrate und Ridge Regression