Vergleich von linearen bayesianischen Regressoren

Dieses Beispiel vergleicht zwei verschiedene bayesianische Regressoren

• ein Automatic Relevance Determination - ARD

• ein Bayesian Ridge Regression

Im ersten Teil verwenden wir ein Ordinary Least Squares (OLS) Modell als Basis, um die Koeffizienten der Modelle mit den tatsächlichen Koeffizienten zu vergleichen. Danach zeigen wir, dass die Schätzung solcher Modelle durch iteratives Maximieren der marginalen Log-Likelihood der Beobachtungen erfolgt.

Im letzten Abschnitt plotten wir Vorhersagen und Unsicherheiten für die ARD- und die Bayesian Ridge-Regressionen unter Verwendung einer polynomialen Merkmalserweiterung, um eine nichtlineare Beziehung zwischen X und y anzupassen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Robustheit der Modelle bei der Wiederherstellung der tatsächlichen Gewichte

Synthetischen Datensatz generieren

Wir generieren einen Datensatz, bei dem X und y linear verknüpft sind: 10 der Merkmale von X werden zur Erzeugung von y verwendet. Die anderen Merkmale sind nicht nützlich für die Vorhersage von y. Darüber hinaus generieren wir einen Datensatz, bei dem n_samples == n_features gilt. Eine solche Einstellung ist für ein OLS-Modell schwierig und führt potenziell zu beliebig großen Gewichten. Ein Priori auf die Gewichte und eine Strafe mildern das Problem. Schließlich wird Gaußsches Rauschen hinzugefügt.

from sklearn.datasets import make_regression

X, y, true_weights = make_regression(
    n_samples=100,
    n_features=100,
    n_informative=10,
    noise=8,
    coef=True,
    random_state=42,
)

Anpassen der Regressoren

Wir passen nun beide bayesianischen Modelle und das OLS an, um später die Koeffizienten der Modelle zu vergleichen.

import pandas as pd

from sklearn.linear_model import ARDRegression, BayesianRidge, LinearRegression

olr = LinearRegression().fit(X, y)
brr = BayesianRidge(compute_score=True, max_iter=30).fit(X, y)
ard = ARDRegression(compute_score=True, max_iter=30).fit(X, y)
df = pd.DataFrame(
    {
        "Weights of true generative process": true_weights,
        "ARDRegression": ard.coef_,
        "BayesianRidge": brr.coef_,
        "LinearRegression": olr.coef_,
    }
)

Plotten der tatsächlichen und geschätzten Koeffizienten

Nun vergleichen wir die Koeffizienten jedes Modells mit den Gewichten des wahren generativen Modells.

import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import SymLogNorm

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-80, vmax=80),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.tight_layout(rect=(0, 0, 1, 0.95))
_ = plt.title("Models' coefficients")

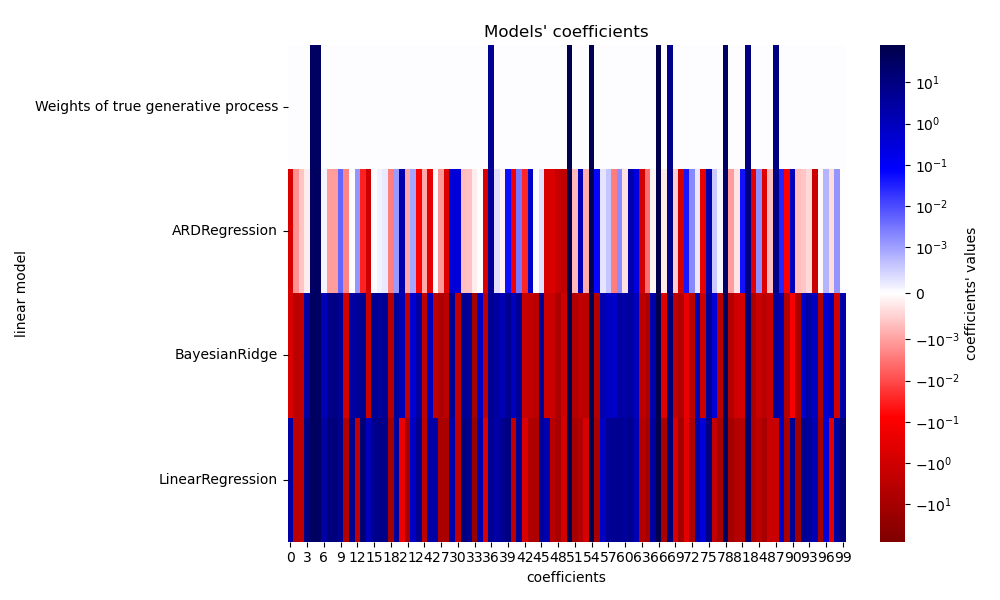
Aufgrund des hinzugefügten Rauschens rekonstruiert keines der Modelle die wahren Gewichte. Tatsächlich haben alle Modelle immer mehr als 10 Koeffizienten ungleich Null. Im Vergleich zum OLS-Schätzer sind die Koeffizienten der Bayesian Ridge-Regression leicht gegen Null verschoben, was sie stabilisiert. Die ARD-Regression liefert eine dünnere Lösung: Einige der nicht-informativen Koeffizienten werden exakt auf Null gesetzt, während andere näher an Null verschoben werden. Einige nicht-informative Koeffizienten sind immer noch vorhanden und behalten große Werte.

Plotten der marginalen Log-Likelihood

import numpy as np

ard_scores = -np.array(ard.scores_)
brr_scores = -np.array(brr.scores_)
plt.plot(ard_scores, color="navy", label="ARD")
plt.plot(brr_scores, color="red", label="BayesianRidge")
plt.ylabel("Log-likelihood")
plt.xlabel("Iterations")
plt.xlim(1, 30)
plt.legend()
_ = plt.title("Models log-likelihood")

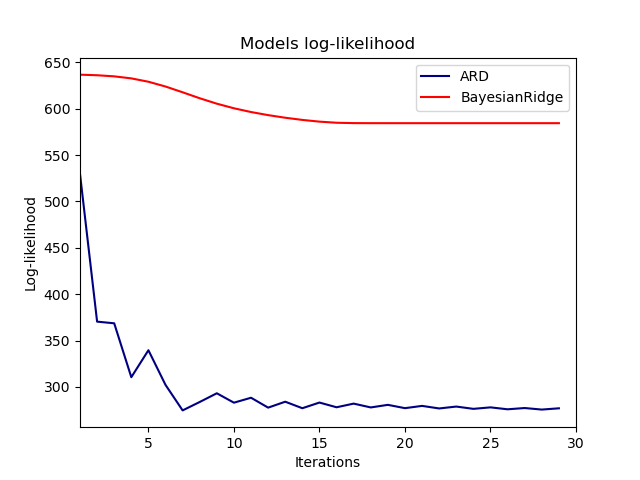
Tatsächlich minimieren beide Modelle die Log-Likelihood bis zu einem willkürlichen Grenzwert, der durch den Parameter max_iter definiert ist.

Bayesianische Regressionen mit polynomialer Merkmalserweiterung

Generieren eines synthetischen Datensatzes

Wir erstellen ein Ziel, das eine nichtlineare Funktion des Eingabemerkmals ist. Rauschen, das einer Standardgleichverteilung folgt, wird hinzugefügt.

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler

rng = np.random.RandomState(0)
n_samples = 110

# sort the data to make plotting easier later
X = np.sort(-10 * rng.rand(n_samples) + 10)
noise = rng.normal(0, 1, n_samples) * 1.35
y = np.sqrt(X) * np.sin(X) + noise
full_data = pd.DataFrame({"input_feature": X, "target": y})
X = X.reshape((-1, 1))

# extrapolation
X_plot = np.linspace(10, 10.4, 10)
y_plot = np.sqrt(X_plot) * np.sin(X_plot)
X_plot = np.concatenate((X, X_plot.reshape((-1, 1))))
y_plot = np.concatenate((y - noise, y_plot))

Anpassen der Regressoren

Hier versuchen wir ein Polynom vom Grad 10, um potenziell zu überanpassen, obwohl die bayesianischen linearen Modelle die Größe der polynomialen Koeffizienten regularisieren. Da fit_intercept=True standardmäßig für ARDRegression und BayesianRidge gilt, sollte PolynomialFeatures kein zusätzliches Bias-Merkmal einführen. Durch Setzen von return_std=True geben die bayesianischen Regressoren die Standardabweichung der Posterior-Verteilung für die Modellparameter zurück.

ard_poly = make_pipeline(
    PolynomialFeatures(degree=10, include_bias=False),
    StandardScaler(),
    ARDRegression(),
).fit(X, y)
brr_poly = make_pipeline(
    PolynomialFeatures(degree=10, include_bias=False),
    StandardScaler(),
    BayesianRidge(),
).fit(X, y)

y_ard, y_ard_std = ard_poly.predict(X_plot, return_std=True)
y_brr, y_brr_std = brr_poly.predict(X_plot, return_std=True)

Plotten von polynomialen Regressionen mit Standardfehlern der Scores

ax = sns.scatterplot(
    data=full_data, x="input_feature", y="target", color="black", alpha=0.75
)
ax.plot(X_plot, y_plot, color="black", label="Ground Truth")
ax.plot(X_plot, y_brr, color="red", label="BayesianRidge with polynomial features")
ax.plot(X_plot, y_ard, color="navy", label="ARD with polynomial features")
ax.fill_between(
    X_plot.ravel(),
    y_ard - y_ard_std,
    y_ard + y_ard_std,
    color="navy",
    alpha=0.3,
)
ax.fill_between(
    X_plot.ravel(),
    y_brr - y_brr_std,
    y_brr + y_brr_std,
    color="red",
    alpha=0.3,
)
ax.legend()
_ = ax.set_title("Polynomial fit of a non-linear feature")

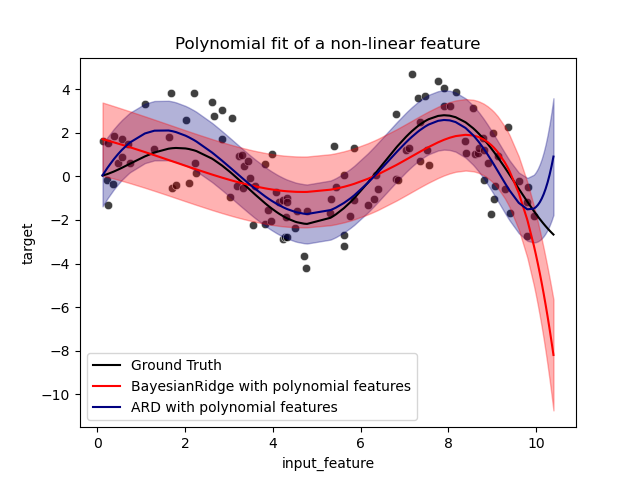
Die Fehlerbalken stellen eine Standardabweichung der vorhergesagten Gaußschen Verteilung der Abfragepunkte dar. Beachten Sie, dass die ARD-Regression die tatsächlichen Werte bei Verwendung der Standardparameter in beiden Modellen am besten erfasst, aber eine weitere Reduzierung des Hyperparameters lambda_init der Bayesian Ridge kann deren Bias reduzieren (siehe Beispiel Kurvenanpassung mit Bayesian Ridge Regression). Aufgrund der inhärenten Einschränkungen einer polynomialen Regression versagen beide Modelle schließlich bei der Extrapolation.

Verwandte Beispiele

L1-basierte Modelle für sparse Signale

L1-basierte Modelle für sparse Signale

Polynomielle und Spline-Interpolation

Polynomielle und Spline-Interpolation

SVM: Gewichtete Stichproben

SVM: Gewichtete Stichproben

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Ridge-Koeffizienten als Funktion der L2-Regularisierung