Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoiden

Dieses Beispiel plottet die Kovarianzellipsoide jeder Klasse und die durch LinearDiscriminantAnalysis (LDA) und QuadraticDiscriminantAnalysis (QDA) gelernte Entscheidungsgrenze. Die Ellipsoide zeigen die zweifache Standardabweichung für jede Klasse. Bei LDA ist die Standardabweichung für alle Klassen gleich, während jede Klasse bei QDA ihre eigene Standardabweichung hat.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datengenerierung

Zuerst definieren wir eine Funktion, um synthetische Daten zu generieren. Sie erstellt zwei Blobs, die bei (0, 0) und (1, 1) zentriert sind. Jedem Blob wird eine bestimmte Klasse zugewiesen. Die Streuung des Blobs wird durch die Parameter cov_class_1 und cov_class_2 gesteuert, die die Kovarianzmatrizen sind, die bei der Generierung der Stichproben aus den Gaußschen Verteilungen verwendet werden.

import numpy as np


def make_data(n_samples, n_features, cov_class_1, cov_class_2, seed=0):
    rng = np.random.RandomState(seed)
    X = np.concatenate(
        [
            rng.randn(n_samples, n_features) @ cov_class_1,
            rng.randn(n_samples, n_features) @ cov_class_2 + np.array([1, 1]),
        ]
    )
    y = np.concatenate([np.zeros(n_samples), np.ones(n_samples)])
    return X, y

Wir generieren drei Datensätze. Im ersten Datensatz teilen sich die beiden Klassen dieselbe Kovarianzmatrix, und diese Kovarianzmatrix hat die Besonderheit, kugelförmig (isoliert) zu sein. Der zweite Datensatz ähnelt dem ersten, erzwingt jedoch nicht die Kugelförmigkeit der Kovarianz. Schließlich hat der dritte Datensatz für jede Klasse eine nicht-kugelförmige Kovarianzmatrix.

covariance = np.array([[1, 0], [0, 1]])
X_isotropic_covariance, y_isotropic_covariance = make_data(
    n_samples=1_000,
    n_features=2,
    cov_class_1=covariance,
    cov_class_2=covariance,
    seed=0,
)
covariance = np.array([[0.0, -0.23], [0.83, 0.23]])
X_shared_covariance, y_shared_covariance = make_data(
    n_samples=300,
    n_features=2,
    cov_class_1=covariance,
    cov_class_2=covariance,
    seed=0,
)
cov_class_1 = np.array([[0.0, -1.0], [2.5, 0.7]]) * 2.0
cov_class_2 = cov_class_1.T
X_different_covariance, y_different_covariance = make_data(
    n_samples=300,
    n_features=2,
    cov_class_1=cov_class_1,
    cov_class_2=cov_class_2,
    seed=0,
)

Plotfunktionen

Der folgende Code wird verwendet, um verschiedene Informationen aus den verwendeten Schätzern zu plotten, nämlich LinearDiscriminantAnalysis (LDA) und QuadraticDiscriminantAnalysis (QDA). Die angezeigten Informationen umfassen

• die Entscheidungsgrenze basierend auf der Wahrscheinlichkeitsschätzung des Schätzers;

• ein Streudiagramm mit Kreisen, die die gut klassifizierten Stichproben darstellen;

• ein Streudiagramm mit Kreuzen, die die falsch klassifizierten Stichproben darstellen;

• den Mittelwert jeder Klasse, geschätzt vom Schätzer, markiert mit einem Stern;

• die geschätzte Kovarianz, dargestellt durch eine Ellipse bei 2 Standardabweichungen vom Mittelwert.

import matplotlib as mpl
from matplotlib import colors

from sklearn.inspection import DecisionBoundaryDisplay


def plot_ellipse(mean, cov, color, ax):
    v, w = np.linalg.eigh(cov)
    u = w[0] / np.linalg.norm(w[0])
    angle = np.arctan(u[1] / u[0])
    angle = 180 * angle / np.pi  # convert to degrees
    # filled Gaussian at 2 standard deviation
    ell = mpl.patches.Ellipse(
        mean,
        2 * v[0] ** 0.5,
        2 * v[1] ** 0.5,
        angle=180 + angle,
        facecolor=color,
        edgecolor="black",
        linewidth=2,
    )
    ell.set_clip_box(ax.bbox)
    ell.set_alpha(0.4)
    ax.add_artist(ell)


def plot_result(estimator, X, y, ax):
    cmap = colors.ListedColormap(["tab:red", "tab:blue"])
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="predict_proba",
        plot_method="pcolormesh",
        ax=ax,
        cmap="RdBu",
        alpha=0.3,
    )
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="predict_proba",
        plot_method="contour",
        ax=ax,
        alpha=1.0,
        levels=[0.5],
    )
    y_pred = estimator.predict(X)
    X_right, y_right = X[y == y_pred], y[y == y_pred]
    X_wrong, y_wrong = X[y != y_pred], y[y != y_pred]
    ax.scatter(X_right[:, 0], X_right[:, 1], c=y_right, s=20, cmap=cmap, alpha=0.5)
    ax.scatter(
        X_wrong[:, 0],
        X_wrong[:, 1],
        c=y_wrong,
        s=30,
        cmap=cmap,
        alpha=0.9,
        marker="x",
    )
    ax.scatter(
        estimator.means_[:, 0],
        estimator.means_[:, 1],
        c="yellow",
        s=200,
        marker="*",
        edgecolor="black",
    )

    if isinstance(estimator, LinearDiscriminantAnalysis):
        covariance = [estimator.covariance_] * 2
    else:
        covariance = estimator.covariance_
    plot_ellipse(estimator.means_[0], covariance[0], "tab:red", ax)
    plot_ellipse(estimator.means_[1], covariance[1], "tab:blue", ax)

    ax.set_box_aspect(1)
    ax.spines["top"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.set(xticks=[], yticks=[])

Vergleich von LDA und QDA

Wir vergleichen die beiden Schätzer LDA und QDA auf allen drei Datensätzen.

import matplotlib.pyplot as plt

from sklearn.discriminant_analysis import (
    LinearDiscriminantAnalysis,
    QuadraticDiscriminantAnalysis,
)

fig, axs = plt.subplots(nrows=3, ncols=2, sharex="row", sharey="row", figsize=(8, 12))

lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
qda = QuadraticDiscriminantAnalysis(solver="svd", store_covariance=True)

for ax_row, X, y in zip(
    axs,
    (X_isotropic_covariance, X_shared_covariance, X_different_covariance),
    (y_isotropic_covariance, y_shared_covariance, y_different_covariance),
):
    lda.fit(X, y)
    plot_result(lda, X, y, ax_row[0])
    qda.fit(X, y)
    plot_result(qda, X, y, ax_row[1])

axs[0, 0].set_title("Linear Discriminant Analysis")
axs[0, 0].set_ylabel("Data with fixed and spherical covariance")
axs[1, 0].set_ylabel("Data with fixed covariance")
axs[0, 1].set_title("Quadratic Discriminant Analysis")
axs[2, 0].set_ylabel("Data with varying covariances")
fig.suptitle(
    "Linear Discriminant Analysis vs Quadratic Discriminant Analysis",
    y=0.94,
    fontsize=15,
)
plt.show()

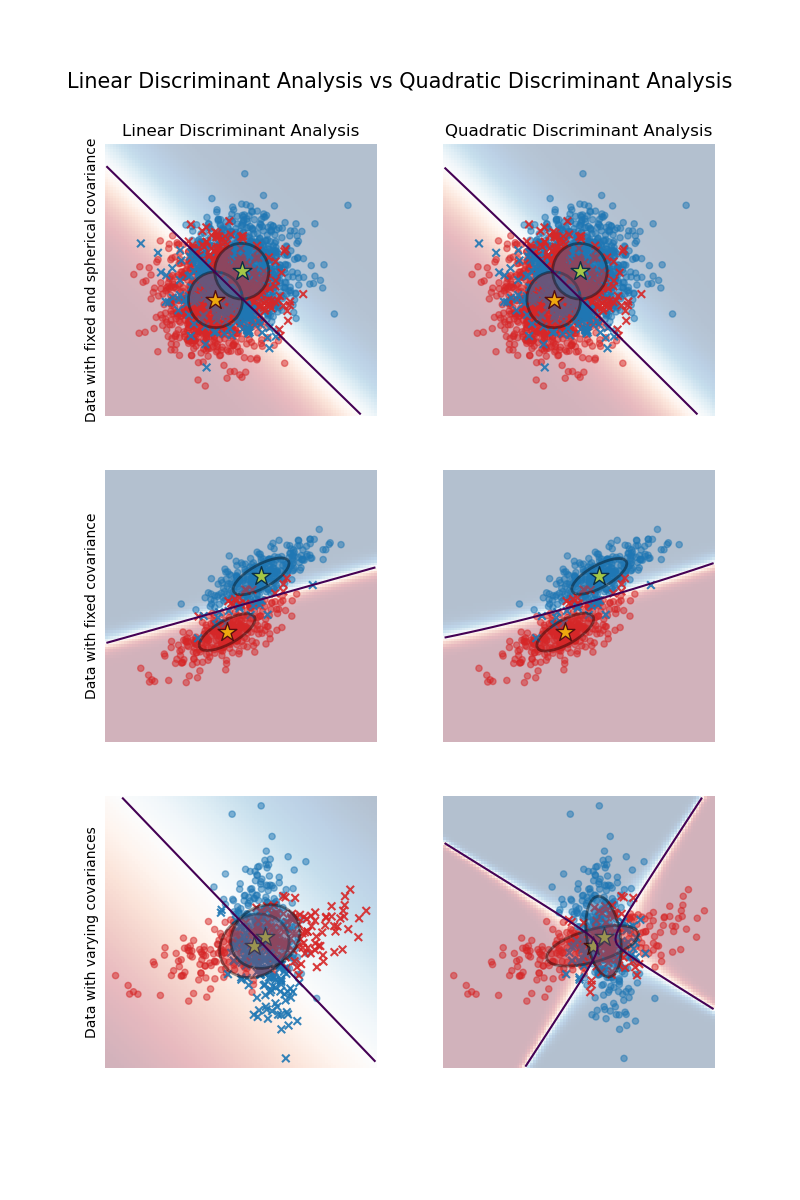
Das erste wichtige Ergebnis ist, dass LDA und QDA für den ersten und zweiten Datensatz äquivalent sind. Tatsächlich besteht der Hauptunterschied darin, dass LDA annimmt, dass die Kovarianzmatrix jeder Klasse gleich ist, während QDA eine Kovarianzmatrix pro Klasse schätzt. Da in diesen Fällen der Datengenerierungsprozess für beide Klassen dieselbe Kovarianzmatrix hat, schätzt QDA zwei Kovarianzmatrizen, die (nahezu) gleich sind und daher der von LDA geschätzten Kovarianzmatrix entsprechen.

Im ersten Datensatz ist die zur Generierung des Datensatzes verwendete Kovarianzmatrix kugelförmig, was zu einer Diskriminanzgrenze führt, die mit der Mittelsenkrechten zwischen den beiden Mittelwerten übereinstimmt. Dies ist beim zweiten Datensatz nicht mehr der Fall. Die Diskriminanzgrenze verläuft nur durch die Mitte der beiden Mittelwerte.

Schließlich beobachten wir im dritten Datensatz den tatsächlichen Unterschied zwischen LDA und QDA. QDA passt zwei Kovarianzmatrizen und liefert eine nichtlineare Diskriminanzgrenze, während LDA unteranpasst, da es davon ausgeht, dass beide Klassen eine einzige Kovarianzmatrix teilen.

Verwandte Beispiele

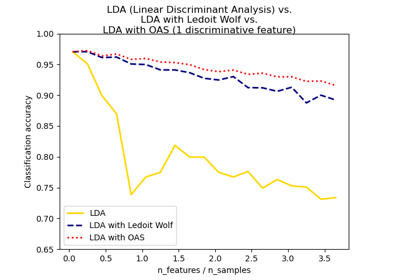
Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Ausreißererkennung auf einem realen Datensatz

Ausreißererkennung auf einem realen Datensatz

Gaußsche Mischmodell-Auswahl

Gaußsche Mischmodell-Auswahl

Robuste vs. Empirische Kovarianzschätzung

Robuste vs. Empirische Kovarianzschätzung