Demonstration der k-means-Annahmen

Dieses Beispiel soll Situationen veranschaulichen, in denen k-means unintuitive und möglicherweise unerwünschte Cluster erzeugt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datengenerierung

Die Funktion make_blobs erzeugt isotrope (sphärische) Gaußsche Blobs. Um anisotrope (elliptische) Gaußsche Blobs zu erhalten, muss eine lineare transformation definiert werden.

import numpy as np

from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # Anisotropic blobs
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # Unequal variance
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

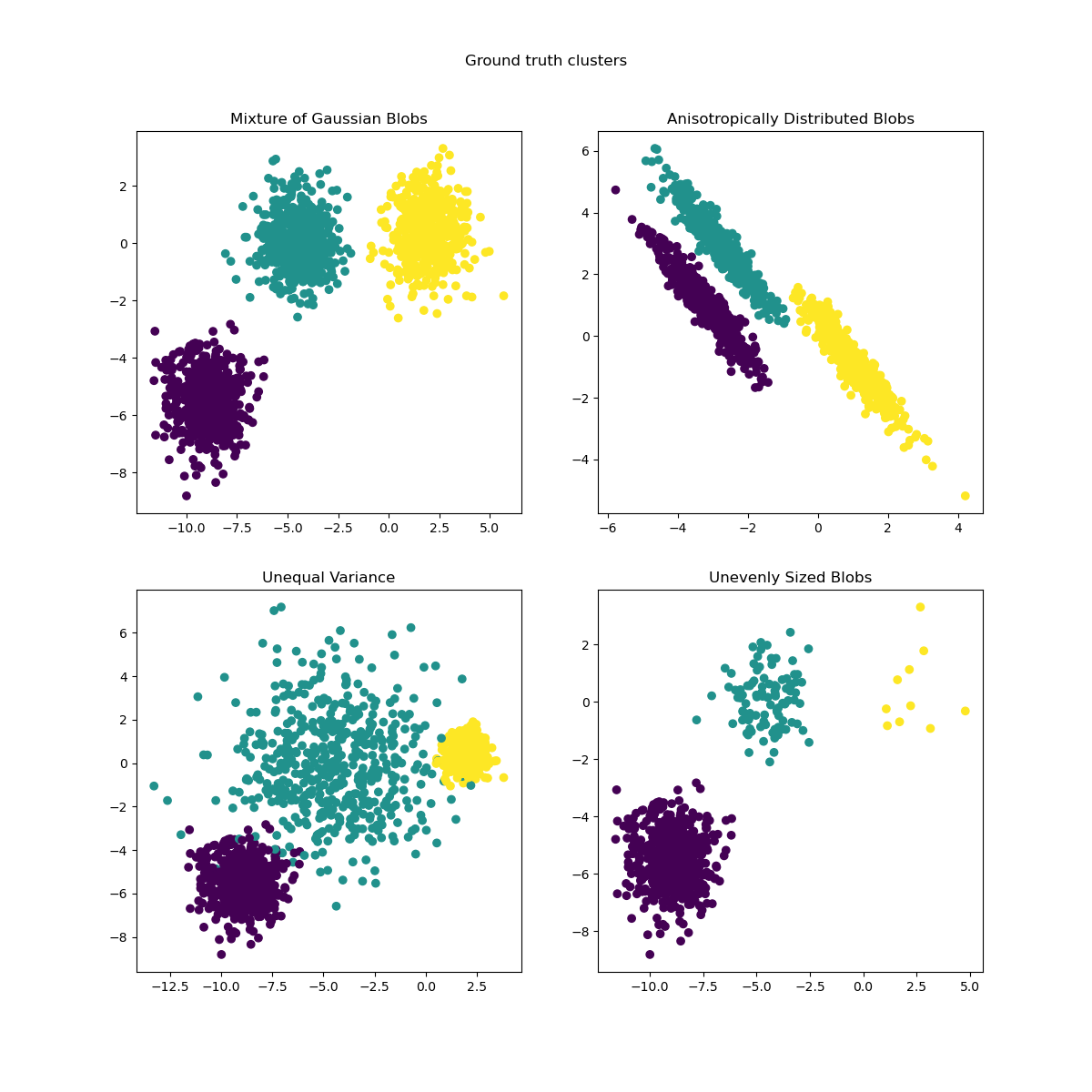
Wir können die resultierenden Daten visualisieren

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("Mixture of Gaussian Blobs")

axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("Unequal Variance")

axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Ground truth clusters").set_y(0.95)
plt.show()

Modelle anpassen und Ergebnisse plotten

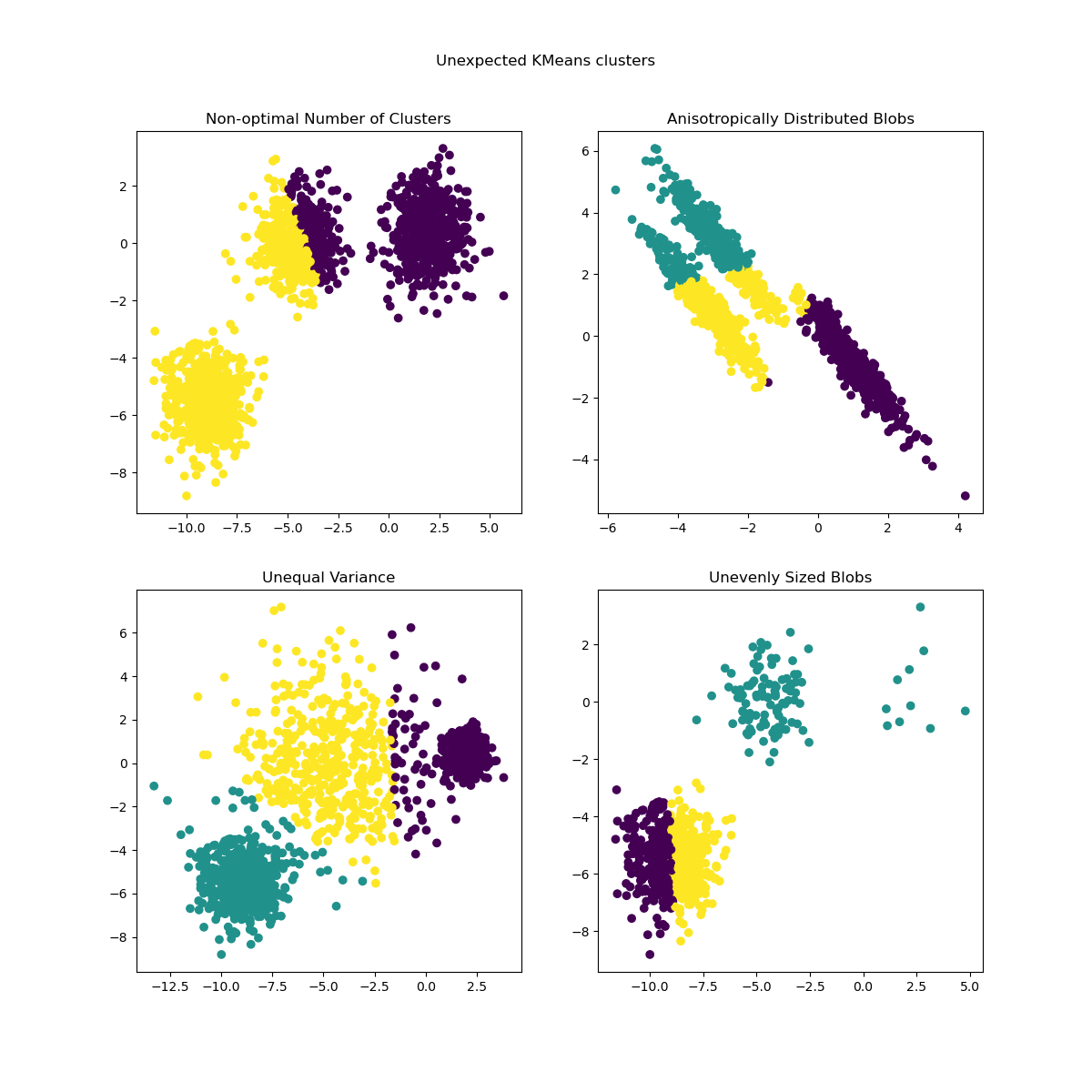
Die zuvor generierten Daten werden nun verwendet, um zu zeigen, wie KMeans in den folgenden Szenarien verhält:

• Nicht-optimale Anzahl von Clustern: In einer realen Umgebung gibt es keine eindeutig definierte **wahre** Anzahl von Clustern. Eine geeignete Anzahl von Clustern muss anhand datenbasierter Kriterien und Kenntnis des beabsichtigten Ziels entschieden werden.

• Anisotrop verteilte Blobs: k-means minimiert die euklidischen Abstände der Samples zum Zentroid des Clusters, dem sie zugeordnet sind. Folglich ist k-means besser für Cluster geeignet, die isotrop und normalverteilt sind (d.h. sphärische Gaußsche Verteilungen).

• Ungleiche Varianz: k-means ist äquivalent zur Schätzung der maximalen Wahrscheinlichkeit für eine "Mischung" von k Gaußschen Verteilungen mit denselben Varianzen, aber möglicherweise unterschiedlichen Mittelwerten.

• Ungleichmäßig große Blobs: Es gibt kein theoretisches Ergebnis für k-means, das besagt, dass es ähnliche Clustergrößen benötigt, um gut zu funktionieren. Die Minimierung der euklidischen Abstände bedeutet jedoch, dass je spärlicher und höherdimensional das Problem ist, desto höher ist die Notwendigkeit, den Algorithmus mit verschiedenen Zentroid-Seeds auszuführen, um ein globales Minimum der Trägheit sicherzustellen.

from sklearn.cluster import KMeans

common_params = {
    "n_init": "auto",
    "random_state": random_state,
}

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

y_pred = KMeans(n_clusters=2, **common_params).fit_predict(X)
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y_pred)
axs[0, 0].set_title("Non-optimal Number of Clusters")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_aniso)
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_varied)
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
axs[1, 0].set_title("Unequal Variance")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_filtered)
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Unexpected KMeans clusters").set_y(0.95)
plt.show()

Mögliche Lösungen

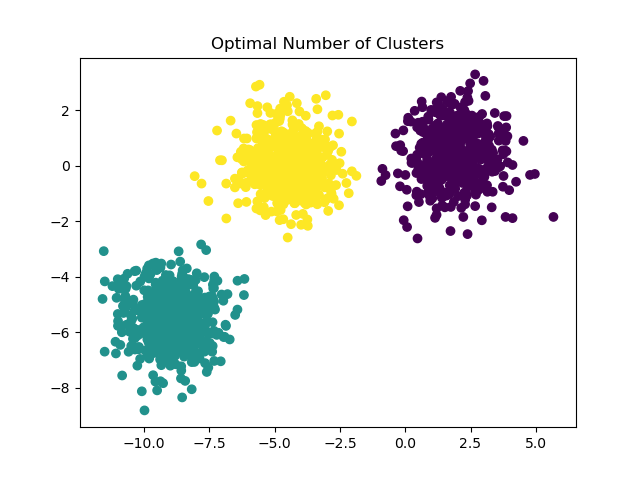
Für ein Beispiel, wie man eine korrekte Anzahl von Blobs findet, siehe Auswahl der Anzahl von Clustern mit Silhouettenanalyse bei KMeans-Clustering. In diesem Fall reicht es aus, n_clusters=3 zu setzen.

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Optimal Number of Clusters")
plt.show()

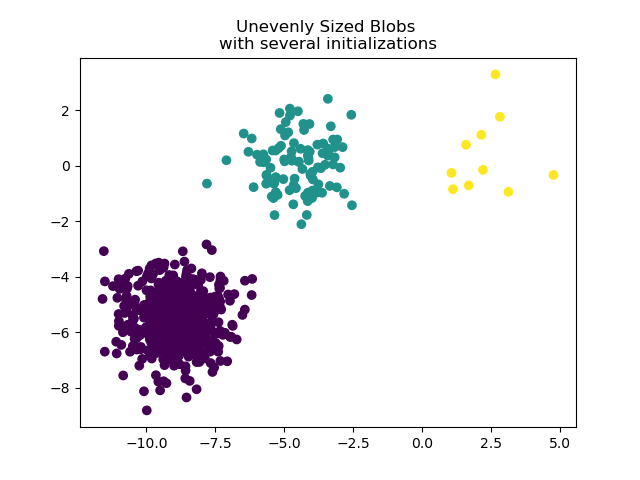
Um ungleichmäßig große Blobs zu handhaben, kann die Anzahl der zufälligen Initialisierungen erhöht werden. In diesem Fall setzen wir n_init=10, um die Konvergenz zu einem sub-optimalen lokalen Minimum zu vermeiden. Weitere Details finden Sie unter Clustering von spärlichen Daten mit k-means.

y_pred = KMeans(n_clusters=3, n_init=10, random_state=random_state).fit_predict(
    X_filtered
)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs \nwith several initializations")
plt.show()

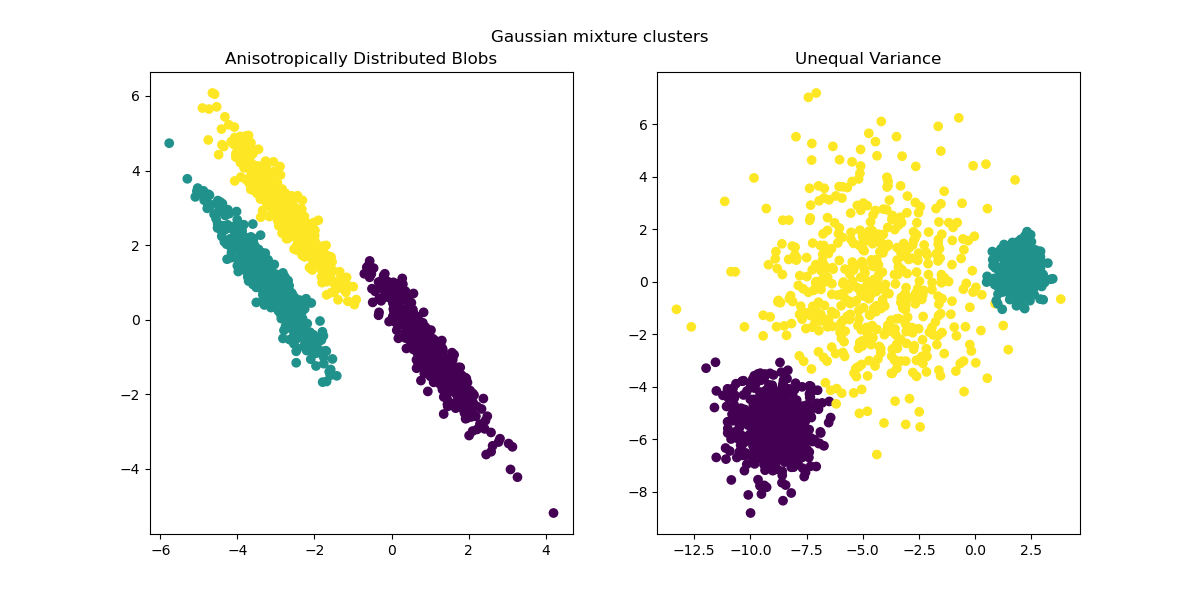
Da anisotrope und ungleiche Varianzen reale Einschränkungen des k-means-Algorithmus darstellen, schlagen wir hier stattdessen die Verwendung von GaussianMixture vor, der ebenfalls Gaußsche Cluster annimmt, aber keine Einschränkungen hinsichtlich ihrer Varianzen auferlegt. Beachten Sie, dass die korrekte Anzahl von Blobs immer noch ermittelt werden muss (siehe Auswahl eines Gaußschen Mischmodells).

Für ein Beispiel, wie andere Clustering-Methoden mit anisotropen oder ungleichen Varianz-Blobs umgehen, siehe das Beispiel Vergleich verschiedener Clustering-Algorithmen auf Beispiel-Datensätzen.

from sklearn.mixture import GaussianMixture

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))

y_pred = GaussianMixture(n_components=3).fit_predict(X_aniso)
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
ax1.set_title("Anisotropically Distributed Blobs")

y_pred = GaussianMixture(n_components=3).fit_predict(X_varied)
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
ax2.set_title("Unequal Variance")

plt.suptitle("Gaussian mixture clusters").set_y(0.95)
plt.show()

Schlussbemerkungen

In hochdimensionalen Räumen werden euklidische Abstände tendenziell aufgebläht (in diesem Beispiel nicht gezeigt). Das Ausführen eines Dimensionsreduktionsalgorithmus vor dem k-means-Clustering kann dieses Problem lindern und die Berechnungen beschleunigen (siehe das Beispiel Clustering von Textdokumenten mit k-means).

Wenn Cluster bekanntermaßen isotrop sind, ähnliche Varianzen aufweisen und nicht zu spärlich sind, ist der k-means-Algorithmus recht effektiv und einer der schnellsten verfügbaren Clustering-Algorithmen. Dieser Vorteil geht verloren, wenn er mehrmals neu gestartet werden muss, um eine Konvergenz zu einem lokalen Minimum zu vermeiden.

Verwandte Beispiele

Vergleich der Leistung von Bisecting K-Means und Regular K-Means

Vergleich der Leistung von Bisecting K-Means und Regular K-Means

Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

Kreuzvalidierte Vorhersagen plotten

Kreuzvalidierte Vorhersagen plotten

Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten

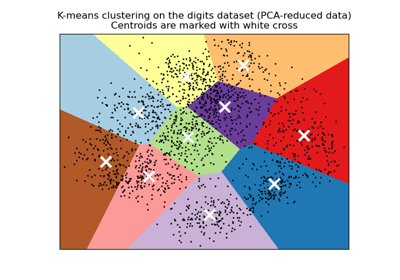
Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten