Hinweis

Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

Kombinieren von Prädiktoren mit Stacking#

Stacking bezieht sich auf eine Methode, um Estimators zu vermischen. Bei dieser Strategie werden einige Estimators individuell auf Trainingsdaten angepasst, während ein endgültiger Estimator mithilfe der gestackten Vorhersagen dieser Basis-Estimators trainiert wird.

In diesem Beispiel veranschaulichen wir den Anwendungsfall, bei dem verschiedene Regressoren zusammen gestapelt werden und ein endgültiger linearer, bestrafter Regressor zur Ausgabe der Vorhersage verwendet wird. Wir vergleichen die Leistung jedes einzelnen Regressors mit der Stacking-Strategie. Stacking verbessert die Gesamtleistung geringfügig.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatz herunterladen#

Wir verwenden den Ames Housing-Datensatz, der zuerst von Dean De Cock zusammengestellt und nach seiner Verwendung in einer Kaggle-Herausforderung bekannter wurde. Es handelt sich um eine Sammlung von 1460 Wohnhäusern in Ames, Iowa, die jeweils durch 80 Merkmale beschrieben werden. Wir werden ihn verwenden, um den endgültigen logarithmischen Preis der Häuser vorherzusagen. In diesem Beispiel werden nur die 20 interessantesten Merkmale verwendet, die mithilfe von GradientBoostingRegressor() ausgewählt wurden, und die Anzahl der Einträge begrenzt (hier gehen wir nicht ins Detail, wie die interessantesten Merkmale ausgewählt werden).

Der Ames Housing-Datensatz wird nicht mit scikit-learn mitgeliefert, daher werden wir ihn von OpenML abrufen.

import numpy as np

from sklearn.datasets import fetch_openml
from sklearn.utils import shuffle


def load_ames_housing():
    df = fetch_openml(name="house_prices", as_frame=True)
    X = df.data
    y = df.target

    features = [
        "YrSold",
        "HeatingQC",
        "Street",
        "YearRemodAdd",
        "Heating",
        "MasVnrType",
        "BsmtUnfSF",
        "Foundation",
        "MasVnrArea",
        "MSSubClass",
        "ExterQual",
        "Condition2",
        "GarageCars",
        "GarageType",
        "OverallQual",
        "TotalBsmtSF",
        "BsmtFinSF1",
        "HouseStyle",
        "MiscFeature",
        "MoSold",
    ]

    X = X.loc[:, features]
    X, y = shuffle(X, y, random_state=0)

    X = X.iloc[:600]
    y = y.iloc[:600]
    return X, np.log(y)


X, y = load_ames_housing()

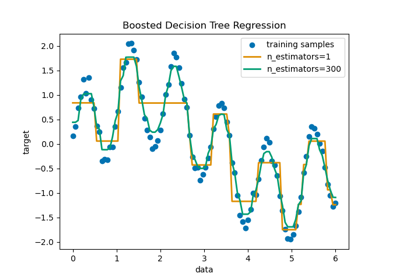
Ergebnisse messen und plotten#

Jetzt können wir den Ames Housing-Datensatz verwenden, um Vorhersagen zu treffen. Wir prüfen die Leistung jedes einzelnen Prädiktors sowie des Stacks der Regressoren.

import time

import matplotlib.pyplot as plt

from sklearn.metrics import PredictionErrorDisplay
from sklearn.model_selection import cross_val_predict, cross_validate

fig, axs = plt.subplots(2, 2, figsize=(9, 7))
axs = np.ravel(axs)

for ax, (name, est) in zip(
    axs, estimators + [("Stacking Regressor", stacking_regressor)]
):
    scorers = {"R2": "r2", "MAE": "neg_mean_absolute_error"}

    start_time = time.time()
    scores = cross_validate(
        est, X, y, scoring=list(scorers.values()), n_jobs=-1, verbose=0
    )
    elapsed_time = time.time() - start_time

    y_pred = cross_val_predict(est, X, y, n_jobs=-1, verbose=0)
    scores = {
        key: (
            f"{np.abs(np.mean(scores[f'test_{value}'])):.2f} +- "
            f"{np.std(scores[f'test_{value}']):.2f}"
        )
        for key, value in scorers.items()
    }

    display = PredictionErrorDisplay.from_predictions(
        y_true=y,
        y_pred=y_pred,
        kind="actual_vs_predicted",
        ax=ax,
        scatter_kwargs={"alpha": 0.2, "color": "tab:blue"},
        line_kwargs={"color": "tab:red"},
    )
    ax.set_title(f"{name}\nEvaluation in {elapsed_time:.2f} seconds")

    for name, score in scores.items():
        ax.plot([], [], " ", label=f"{name}: {score}")
    ax.legend(loc="upper left")

plt.suptitle("Single predictors versus stacked predictors")
plt.tight_layout()
plt.subplots_adjust(top=0.9)
plt.show()

Single predictors versus stacked predictors, Random Forest Evaluation in 0.90 seconds, Lasso Evaluation in 0.21 seconds, Gradient Boosting Evaluation in 0.41 seconds, Stacking Regressor Evaluation in 8.07 seconds

Der gestapelte Regressor kombiniert die Stärken der verschiedenen Regressoren. Wir sehen jedoch auch, dass das Trainieren des gestapelten Regressors wesentlich rechenintensiver ist.

Gesamtlaufzeit des Skripts: (0 Minuten 19,441 Sekunden)

Verwandte Beispiele

Vorhersagen von einzelnen und abstimmenden Regressionsmodellen plotten

Schätzer und komplexe Pipelines anzeigen

Unterstützung für kategorische Merkmale in Gradient Boosting

Entscheidungsbaum-Regression mit AdaBoost

Galerie generiert von Sphinx-Gallery

	transformers transformers: list of tuples Liste von Tupeln (name, transformer, columns), die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden. name : str Wie in Pipeline und FeatureUnion erlaubt dies, den Transformer und seine Parameter mit ``set_params`` zu setzen und in der Gitter-Suche zu durchsuchen. transformer : {'drop', 'passthrough'} oder estimator Der Estimator muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten gelöscht oder unverändert durchgelassen werden sollen. columns : str, array-like von str, int, array-like von int, array-like von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganze Zahlen werden als positionsbezogene Spalten interpretiert, während Zeichenketten DataFrame-Spalten nach Namen referenzieren können. Eine skalare Zeichenkette oder ganze Zahl sollte verwendet werden, wenn ``transformer`` erwartet, dass X ein 1D-Array-ähnliches Objekt (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein callable erhält die Eingabedaten `X` und kann beliebige der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('simpleimputer', ...), ('ordinalencoder', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'drop'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, wird :meth:`ColumnTransformer.get_feature_names_out` allen Feature-Namen das Präfix des Namens des Transformers voranstellen, der dieses Feature generiert hat. Es ist äquivalent zu `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Feature-Namen präfixieren und einen Fehler ausgeben, wenn Feature-Namen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, wird :meth:`ColumnTransformer.get_feature_names_out` alle Features mit dem Namen des Transformers umbenennen. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Feature-Name. Die zurückgegebene Zeichenkette ist der neue Feature-Name. - Wenn ``str``, muss es sich um eine formatierbare Zeichenkette handeln. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe die Methode :meth:`str.format` aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein callable oder eine formatierbare Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	missing_values missing_values: int, float, str, np.nan, None oder pandas.NA, Standard=np.nan Der Platzhalter für die fehlenden Werte. Alle Vorkommen von `missing_values` werden imputiert. Für Pandas-DataFrames mit nullbaren Integer-Datentypen mit fehlenden Werten kann `missing_values` auf `np.nan` oder `pd.NA` gesetzt werden.	nan
	strategy strategy: str oder Callable, Standardwert='mean' Die Imputationsstrategie. - Wenn "mean", dann fehlende Werte mit dem Mittelwert entlang jeder Spalte ersetzen. Kann nur mit numerischen Daten verwendet werden. - Wenn "median", dann fehlende Werte mit dem Median entlang jeder Spalte ersetzen. Kann nur mit numerischen Daten verwendet werden. - Wenn "most_frequent", dann fehlende Werte mit dem häufigsten Wert entlang jeder Spalte ersetzen. Kann mit Zeichenketten oder numerischen Daten verwendet werden. Wenn es mehr als einen solchen Wert gibt, wird nur der kleinste zurückgegeben. - Wenn "constant", dann fehlende Werte mit fill_value ersetzen. Kann mit Zeichenketten oder numerischen Daten verwendet werden. - Wenn eine Instanz von Callable, dann fehlende Werte mit der skalaren Statistik ersetzen, die durch Ausführen des Callables über ein dichtes 1D- Array mit nicht fehlenden Werten jeder Spalte zurückgegeben wird. .. versionadded:: 0.20 strategy="constant" für die Ersetzung durch einen festen Wert. .. versionadded:: 1.5 strategy=callable für benutzerdefinierte Wert-Imputation.	'mean'
	fill_value fill_value: str oder numerischer Wert, Standard=None Wenn strategy == "constant", wird `fill_value` verwendet, um alle Vorkommen von missing_values zu ersetzen. Für Zeichenketten oder Objekt-Datentypen muss `fill_value` eine Zeichenkette sein. Wenn `None`, ist `fill_value` 0 bei der Imputation numerischer Daten und "missing_value" für Zeichenketten oder Objekt-Datentypen.	None
	copy copy: bool, Standard=True Wenn True, wird eine Kopie von X erstellt. Wenn False, wird die Imputation nach Möglichkeit direkt durchgeführt. Beachten Sie, dass in den folgenden Fällen immer eine neue Kopie erstellt wird, auch wenn `copy=False` - Wenn `X` kein Array von Fließkommawerten ist; - Wenn `X` als CSR-Matrix kodiert ist; - Wenn `add_indicator=True`.	True
	add_indicator add_indicator: bool, Standard=False Wenn True, wird ein :class:`MissingIndicator` Transform an die Ausgabe des Imputers angehängt. Dies ermöglicht einem prädiktiven Schätzer, Fehlwerte trotz Imputation zu berücksichtigen. Wenn ein Merkmal zur Fit-/Trainingszeit keine fehlenden Werte hat, erscheint das Merkmal nicht im Fehlwertindikator, auch wenn zur Transformations-/Testzeit fehlende Werte vorhanden sind.	True
	keep_empty_features keep_empty_features: bool, Standard=False Wenn True, werden Merkmale, die ausschließlich aus fehlenden Werten bestehen, wenn `fit` aufgerufen wird, in den Ergebnissen zurückgegeben, wenn `transform` aufgerufen wird. Der imputierte Wert ist immer `0`, außer wenn `strategy="constant"`, in diesem Fall wird stattdessen `fill_value` verwendet. .. versionadded:: 1.2	False

	categories categories: 'auto' oder eine Liste von array-ähnlichen Objekten, default='auto' Kategorien (eindeutige Werte) pro Merkmal: - 'auto' : Kategorien werden automatisch aus den Trainingsdaten bestimmt. - Liste : ``categories[i]`` enthält die erwarteten Kategorien in der i-ten Spalte. Die übergebenen Kategorien sollten keine Strings und numerischen Werte mischen und sollten bei numerischen Werten sortiert sein. Die verwendeten Kategorien finden Sie im Attribut ``categories_``.	'auto'
	dtype dtype: numerischer Typ, default=np.float64 Gewünschter dtype der Ausgabe.	<class 'numpy.float64'>
	handle_unknown handle_unknown: {'error', 'use_encoded_value'}, default='error' Wenn auf 'error' gesetzt, wird ein Fehler ausgelöst, wenn während des Transforms eine unbekannte kategoriale Funktion vorhanden ist. Wenn auf 'use_encoded_value' gesetzt, wird der kodierte Wert unbekannter Kategorien auf den Wert gesetzt, der für den Parameter `unknown_value` angegeben wurde. Im :meth:`inverse_transform` wird eine unbekannte Kategorie als None dargestellt. .. versionadded:: 0.24	'use_encoded_value'
	unknown_value unknown_value: int oder np.nan, default=None Wenn der Parameter handle_unknown auf 'use_encoded_value' gesetzt ist, ist dieser Parameter erforderlich und setzt den kodierten Wert unbekannter Kategorien. Er muss sich von den Werten unterscheiden, die zum Kodieren von Kategorien in `fit` verwendet wurden. Wenn er auf np.nan gesetzt ist, muss der `dtype`-Parameter einen Fließkomma-dtype haben. .. versionadded:: 0.24	-1
	encoded_missing_value encoded_missing_value: int oder np.nan, default=np.nan Kodierter Wert für fehlende Kategorien. Wenn auf `np.nan` gesetzt, muss der `dtype`-Parameter einen Fließkomma-dtype haben. .. versionadded:: 1.1	-2
	min_frequency min_frequency: int oder float, default=None Gibt die Mindesthäufigkeit an, unterhalb derer eine Kategorie als wenig häufig gilt. - Wenn `int`, gelten Kategorien mit geringerer Kardinalität als wenig häufig. - Wenn `float`, gelten Kategorien mit geringerer Kardinalität als `min_frequency * n_samples` als wenig häufig. .. versionadded:: 1.3 Weiterlesen im :ref:`Benutzerhandbuch `.	None
	max_categories max_categories: int, default=None Gibt eine Obergrenze für die Anzahl der Ausgabekategorien für jedes Eingabemerkmal an, wenn wenig häufige Kategorien berücksichtigt werden. Wenn wenig häufige Kategorien vorhanden sind, enthält `max_categories` die Kategorie, die die wenig häufigen Kategorien repräsentiert, zusammen mit den häufigen Kategorien. Wenn `None`, gibt es keine Obergrenze für die Anzahl der Ausgabemerkmale. `max_categories` berücksichtigt keine fehlenden oder unbekannten Kategorien. Das Setzen von `unknown_value` oder `encoded_missing_value` auf eine Ganzzahl erhöht die Anzahl der eindeutigen Ganzzahlcodes um jeweils eins. Dies kann zu bis zu `max_categories + 2` Ganzzahlcodes führen. .. versionadded:: 1.3 Weiterlesen im :ref:`Benutzerhandbuch `.	None

	transformers transformers: list of tuples Liste von Tupeln (name, transformer, columns), die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden. name : str Wie in Pipeline und FeatureUnion erlaubt dies, den Transformer und seine Parameter mit ``set_params`` zu setzen und in der Gitter-Suche zu durchsuchen. transformer : {'drop', 'passthrough'} oder estimator Der Estimator muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten gelöscht oder unverändert durchgelassen werden sollen. columns : str, array-like von str, int, array-like von int, array-like von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganze Zahlen werden als positionsbezogene Spalten interpretiert, während Zeichenketten DataFrame-Spalten nach Namen referenzieren können. Eine skalare Zeichenkette oder ganze Zahl sollte verwendet werden, wenn ``transformer`` erwartet, dass X ein 1D-Array-ähnliches Objekt (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein callable erhält die Eingabedaten `X` und kann beliebige der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('pipeline', ...), ('onehotencoder', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'drop'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, wird :meth:`ColumnTransformer.get_feature_names_out` allen Feature-Namen das Präfix des Namens des Transformers voranstellen, der dieses Feature generiert hat. Es ist äquivalent zu `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Feature-Namen präfixieren und einen Fehler ausgeben, wenn Feature-Namen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, wird :meth:`ColumnTransformer.get_feature_names_out` alle Features mit dem Namen des Transformers umbenennen. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Feature-Name. Die zurückgegebene Zeichenkette ist der neue Feature-Name. - Wenn ``str``, muss es sich um eine formatierbare Zeichenkette handeln. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe die Methode :meth:`str.format` aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein callable oder eine formatierbare Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	missing_values missing_values: int, float, str, np.nan, None oder pandas.NA, Standard=np.nan Der Platzhalter für die fehlenden Werte. Alle Vorkommen von `missing_values` werden imputiert. Für Pandas-DataFrames mit nullbaren Integer-Datentypen mit fehlenden Werten kann `missing_values` auf `np.nan` oder `pd.NA` gesetzt werden.	nan
	strategy strategy: str oder Callable, Standardwert='mean' Die Imputationsstrategie. - Wenn "mean", dann fehlende Werte mit dem Mittelwert entlang jeder Spalte ersetzen. Kann nur mit numerischen Daten verwendet werden. - Wenn "median", dann fehlende Werte mit dem Median entlang jeder Spalte ersetzen. Kann nur mit numerischen Daten verwendet werden. - Wenn "most_frequent", dann fehlende Werte mit dem häufigsten Wert entlang jeder Spalte ersetzen. Kann mit Zeichenketten oder numerischen Daten verwendet werden. Wenn es mehr als einen solchen Wert gibt, wird nur der kleinste zurückgegeben. - Wenn "constant", dann fehlende Werte mit fill_value ersetzen. Kann mit Zeichenketten oder numerischen Daten verwendet werden. - Wenn eine Instanz von Callable, dann fehlende Werte mit der skalaren Statistik ersetzen, die durch Ausführen des Callables über ein dichtes 1D- Array mit nicht fehlenden Werten jeder Spalte zurückgegeben wird. .. versionadded:: 0.20 strategy="constant" für die Ersetzung durch einen festen Wert. .. versionadded:: 1.5 strategy=callable für benutzerdefinierte Wert-Imputation.	'mean'
	fill_value fill_value: str oder numerischer Wert, Standard=None Wenn strategy == "constant", wird `fill_value` verwendet, um alle Vorkommen von missing_values zu ersetzen. Für Zeichenketten oder Objekt-Datentypen muss `fill_value` eine Zeichenkette sein. Wenn `None`, ist `fill_value` 0 bei der Imputation numerischer Daten und "missing_value" für Zeichenketten oder Objekt-Datentypen.	None
	copy copy: bool, Standard=True Wenn True, wird eine Kopie von X erstellt. Wenn False, wird die Imputation nach Möglichkeit direkt durchgeführt. Beachten Sie, dass in den folgenden Fällen immer eine neue Kopie erstellt wird, auch wenn `copy=False` - Wenn `X` kein Array von Fließkommawerten ist; - Wenn `X` als CSR-Matrix kodiert ist; - Wenn `add_indicator=True`.	True
	add_indicator add_indicator: bool, Standard=False Wenn True, wird ein :class:`MissingIndicator` Transform an die Ausgabe des Imputers angehängt. Dies ermöglicht einem prädiktiven Schätzer, Fehlwerte trotz Imputation zu berücksichtigen. Wenn ein Merkmal zur Fit-/Trainingszeit keine fehlenden Werte hat, erscheint das Merkmal nicht im Fehlwertindikator, auch wenn zur Transformations-/Testzeit fehlende Werte vorhanden sind.	True
	keep_empty_features keep_empty_features: bool, Standard=False Wenn True, werden Merkmale, die ausschließlich aus fehlenden Werten bestehen, wenn `fit` aufgerufen wird, in den Ergebnissen zurückgegeben, wenn `transform` aufgerufen wird. Der imputierte Wert ist immer `0`, außer wenn `strategy="constant"`, in diesem Fall wird stattdessen `fill_value` verwendet. .. versionadded:: 1.2	False

Kombinieren von Prädiktoren mit Stacking#

Datensatz herunterladen#

Pipeline zur Vorverarbeitung der Daten erstellen#

Stack von Prädiktoren auf einem einzelnen Datensatz#

Ergebnisse messen und plotten#

Diese Seite

	copy copy: bool, Standard=True Wenn False, versuchen Sie, eine Kopie zu vermeiden und stattdessen direkt zu skalieren. Dies ist nicht garantiert, dass es immer direkt funktioniert; z.B. wenn die Daten kein NumPy-Array oder eine scipy.sparse CSR-Matrix sind, kann immer noch eine Kopie zurückgegeben werden.	True
	with_mean with_mean: bool, Standard=True Wenn True, zentrieren Sie die Daten vor der Skalierung. Dies funktioniert nicht (und löst eine Ausnahme aus), wenn versucht, auf Sparse-Matrizen angewendet zu werden, da deren Zentrierung den Aufbau einer dichten Matrix erfordert, die in gängigen Anwendungsfällen wahrscheinlich zu groß ist, um in den Speicher zu passen.	True
	with_std with_std: bool, Standard=True Wenn True, skalieren Sie die Daten auf Einheitsvarianz (oder äquivalent, Einheitsstandardabweichung).	True

	categories categories: 'auto' oder eine Liste von Arrays, Standard='auto' Kategorien (eindeutige Werte) pro Merkmal: - 'auto': Kategorien automatisch aus den Trainingsdaten ermitteln. - Liste: ``categories[i]`` enthält die erwarteten Kategorien in der i-ten Spalte. Die übergebenen Kategorien sollten keine Strings und numerischen Werte innerhalb eines Merkmals mischen und sollten bei numerischen Werten sortiert sein. Die verwendeten Kategorien finden Sie im Attribut ``categories_``. .. versionadded:: 0.20	'auto'
	drop drop: {'first', 'if_binary'} oder array-like der Form (n_features,), Standardwert=None Spezifiziert eine Methodik zur Löschung einer der Kategorien pro Merkmal. Dies ist nützlich in Situationen, in denen perfekt kollineare Merkmale Probleme verursachen, z.B. beim Einspeisen der resultierenden Daten in ein unregularisiertes lineares Regressionsmodell. Das Löschen einer Kategorie bricht jedoch die Symmetrie der ursprünglichen Darstellung und kann daher einen Bias in nachgeschalteten Modellen erzeugen, z.B. für bestrafte lineare Klassifikations- oder Regressionsmodelle. - None : Alle Merkmale beibehalten (Standard). - 'first' : Lösche die erste Kategorie in jedem Merkmal. Wenn nur eine Kategorie vorhanden ist, wird das Merkmal vollständig gelöscht. - 'if_binary' : Lösche die erste Kategorie in jedem Merkmal mit zwei Kategorien. Merkmale mit 1 oder mehr als 2 Kategorien bleiben unverändert. - array : ``drop[i]`` ist die Kategorie im Merkmal ``X[:, i]``, die gelöscht werden soll. Wenn `max_categories` oder `min_frequency` konfiguriert sind, um seltene Kategorien zu gruppieren, wird das Löschverhalten nach der Gruppierung behandelt. .. versionadded:: 0.21 Der Parameter `drop` wurde in 0.21 hinzugefügt. .. versionchanged:: 0.23 Die Option `drop='if_binary'` wurde in 0.23 hinzugefügt. .. versionchanged:: 1.1 Unterstützung für das Löschen von seltenen Kategorien.	None
	sparse_output sparse_output: bool, Standard=True Wenn ``True``, wird eine :class:`scipy.sparse.csr_matrix` zurückgegeben, d. h. eine spärliche Matrix im "Compressed Sparse Row" (CSR)-Format. .. versionadded:: 1.2 `sparse` wurde in `sparse_output` umbenannt.	True
	dtype dtype: numerischer Typ, default=np.float64 Gewünschter dtype der Ausgabe.	<class 'numpy.float64'>
	handle_unknown handle_unknown: {'error', 'ignore', 'infrequent_if_exist', 'warn'}, Standardwert='error' Spezifiziert die Art und Weise, wie unbekannte Kategorien während :meth:`transform` behandelt werden. - 'error' : Löst einen Fehler aus, wenn während der Transformation eine unbekannte Kategorie vorhanden ist. - 'ignore' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, sind die resultierenden One-Hot-kodierten Spalten für dieses Merkmal alle Null. Bei der inversen Transformation wird eine unbekannte Kategorie als None dargestellt. - 'infrequent_if_exist' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, werden die resultierenden One-Hot-kodierten Spalten für dieses Merkmal der seltenen Kategorie zugeordnet, falls sie existiert. Die seltene Kategorie wird der letzten Position in der Kodierung zugeordnet. Bei der inversen Transformation wird eine unbekannte Kategorie der Kategorie zugeordnet, die als `'infrequent'` bezeichnet wird, falls sie existiert. Wenn die Kategorie `'infrequent'` nicht existiert, dann werden :meth:`transform` und :meth:`inverse_transform` eine unbekannte Kategorie wie bei `handle_unknown='ignore'` behandeln. Seltene Kategorien existieren basierend auf `min_frequency` und `max_categories`. Lesen Sie mehr im :ref:`Benutzerhandbuch `. - 'warn' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, wird eine Warnung ausgegeben und die Kodierung wird dann wie für `handle_unknown="infrequent_if_exist"` beschrieben fortgesetzt. .. versionchanged:: 1.1 `'infrequent_if_exist'` wurde hinzugefügt, um unbekannte Kategorien und seltene Kategorien automatisch zu behandeln. .. versionadded:: 1.6 Die Option `"warn"` wurde in 1.6 hinzugefügt.	'ignore'
	min_frequency min_frequency: int oder float, Standard=None Gibt die minimale Häufigkeit an, unterhalb derer eine Kategorie als selten betrachtet wird. - Wenn `int`, werden Kategorien mit geringerer Kardinalität als selten betrachtet. - Wenn `float`, werden Kategorien mit geringerer Kardinalität als `min_frequency * n_samples` als selten betrachtet. .. versionadded:: 1.1 Lesen Sie mehr im :ref:`Benutzerhandbuch `.	None
	max_categories max_categories: int, Standard=None Gibt eine Obergrenze für die Anzahl der Ausgabemerkmale pro Eingabe- Merkmal an, wenn seltene Kategorien berücksichtigt werden. Wenn es seltene Kategorien gibt, enthält `max_categories` die Kategorie, die die seltenen Kategorien repräsentiert, zusammen mit den häufigen Kategorien. Wenn `None`, gibt es keine Grenze für die Anzahl der Ausgabemerkmale. .. versionadded:: 1.1 Lesen Sie mehr im :ref:`Benutzerhandbuch `.	None
	feature_name_combiner feature_name_combiner: "concat" oder aufrufbar, Standard="concat" Aufrufbare Funktion mit der Signatur `def callable(input_feature, category)`, die einen String zurückgibt. Dies wird verwendet, um Merkmalsnamen zu erstellen, die von :meth:`get_feature_names_out` zurückgegeben werden. `"concat"` verkettet den kodierten Merkmalnamen und die Kategorie mit `feature + "_" + str(category)`. Z. B. erstellt das Merkmal X mit Werten 1, 6, 7 Merkmalnamen `X_1, X_6, X_7`. .. versionadded:: 1.3	'concat'

	steps steps: list of tuples Liste von Tupeln (Name des Schritts, Schätzer), die in sequenzieller Reihenfolge verkettet werden sollen. Um mit der scikit-learn API kompatibel zu sein, müssen alle Schritte `fit` definieren. Alle nicht letzten Schritte müssen auch `transform` definieren. Siehe :ref:`Kombination von Schätzern ` für weitere Details.	[('columntransformer', ...), ('lassocv', ...)]
	transform_input transform_input: list of str, default=None Die Namen der :term:`Metadaten`-Parameter, die von der Pipeline transformiert werden sollen, bevor sie an den Schritt übergeben werden, der sie benötigt. Dies ermöglicht die Transformation einiger Eingabeparameter zu ``fit`` (außer ``X``), die von den Schritten der Pipeline bis zu dem Schritt transformiert werden, der sie benötigt. Die Anforderung wird über :ref:`Metadaten-Routing ` definiert. Dies kann beispielsweise verwendet werden, um einen Validierungsdatensatz durch die Pipeline zu leiten. Sie können dies nur festlegen, wenn das Metadaten-Routing aktiviert ist, was Sie mit ``sklearn.set_config(enable_metadata_routing=True)`` aktivieren können. .. versionadded:: 1.6	None
	memory memory: str oder Objekt mit der joblib.Memory-Schnittstelle, default=None Wird zum Zwischenspeichern der angepassten Transformer der Pipeline verwendet. Der letzte Schritt wird niemals zwischengespeichert, auch wenn es sich um einen Transformer handelt. Standardmäßig erfolgt keine Zwischenspeicherung. Wenn ein String angegeben wird, ist dies der Pfad zum Zwischenspeicherverzeichnis. Durch Aktivieren der Zwischenspeicherung wird eine Kopie der Transformer vor dem Anpassen ausgelöst. Daher kann die an die Pipeline übergebene Transformer-Instanz nicht direkt inspiziert werden. Verwenden Sie das Attribut `named_steps` oder `steps`, um Schätzer innerhalb der Pipeline zu inspizieren. Das Zwischenspeichern der Transformer ist vorteilhaft, wenn das Anpassen zeitaufwändig ist. Siehe :ref:`sphx_glr_auto_examples_neighbors_plot_caching_nearest_neighbors.py` für ein Beispiel zur Aktivierung der Zwischenspeicherung.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Schritts gedruckt, wenn es abgeschlossen ist.	False

	eps eps: float, Standardwert=1e-3 Länge des Pfades. ``eps=1e-3`` bedeutet, dass ``alpha_min / alpha_max = 1e-3``.	0.001
	n_alphas n_alphas: int, Standardwert=100 Anzahl der zu testenden Alphas entlang des Regularisierungspfades. .. deprecated:: 1.7 `n_alphas` wurde in 1.7 als veraltet markiert und wird in 1.9 entfernt. Verwenden Sie stattdessen `alphas`.	'deprecated'
	alphas alphas: array-like oder int, Standardwert=None Werte von Alphas, die entlang des Regularisierungspfades getestet werden sollen. Wenn int, werden `alphas`-Werte automatisch generiert. Wenn array-like, Liste von zu verwendenden Alpha-Werten. .. versionchanged:: 1.7 `alphas` akzeptiert einen ganzzahligen Wert, der die Notwendigkeit der Angabe von `n_alphas` beseitigt. .. deprecated:: 1.7 `alphas=None` wurde in 1.7 als veraltet markiert und wird in 1.9 entfernt, wo der Standardwert auf 100 gesetzt wird.	'warn'
	fit_intercept fit_intercept: bool, Standardwert=True Ob der Achsenabschnitt für dieses Modell berechnet werden soll. Wenn auf False gesetzt, wird kein Achsenabschnitt bei den Berechnungen verwendet (d.h. die Daten werden als zentriert erwartet).	True
	precompute precompute: 'auto', bool oder array-like der Form (n_features, n_features), Standardwert='auto' Ob eine vorab berechnete Gram-Matrix verwendet werden soll, um Berechnungen zu beschleunigen. Wenn auf ``'auto'`` gesetzt, lassen Sie uns entscheiden. Die Gram-Matrix kann auch als Argument übergeben werden.	'auto'
	max_iter max_iter: int, Standardwert=1000 Die maximale Anzahl von Iterationen.	1000
	tol tol: float, Standardwert=1e-4 Die Toleranz für die Optimierung: wenn die Aktualisierungen kleiner oder gleich ``tol`` sind, prüft der Optimierungscode die duale Lücke auf Optimalität und setzt fort, bis diese kleiner oder gleich ``tol`` ist.	0.0001
	copy_X copy_X: bool, Standardwert=True Wenn ``True``, wird X kopiert; andernfalls kann es überschrieben werden.	True
	cv cv: int, Kreuzvalidierungsgenerator oder iterierbar, Standardwert=None Bestimmt die Strategie der Kreuzvalidierungsteilung. Mögliche Eingaben für cv sind: - None, um die standardmäßige 5-fache Kreuzvalidierung zu verwenden, - int, um die Anzahl der Folds anzugeben. - :term:`CV-Teiler`, - Ein iterierbares Objekt, das (train, test) Splits als Array von Indizes liefert. Für ganzzahlige/None-Eingaben wird :class:`~sklearn.model_selection.KFold` verwendet. Siehe das :ref:`Benutzerhandbuch ` für die verschiedenen Kreuzvalidierungsstrategien, die hier verwendet werden können. .. versionchanged:: 0.22 Der Standardwert von ``cv``, wenn None, änderte sich von 3-fach zu 5-fach.	None
	verbose verbose: bool oder int, Standardwert=False Umfang der Ausführlichkeit.	False
	n_jobs n_jobs: int, Standardwert=None Anzahl der CPUs, die während der Kreuzvalidierung verwendet werden sollen. ``None`` bedeutet 1, es sei denn, Sie befinden sich in einem :obj:`joblib.parallel_backend`-Kontext. ``-1`` bedeutet die Verwendung aller Prozessoren. Siehe :term:`Glossar ` für weitere Details.	None
	positive positive: bool, Standardwert=False Wenn positiv, werden die Regressionskoeffizienten auf positiv beschränkt.	False
	random_state random_state: int, RandomState-Instanz, Standardwert=None Der Seed des Pseudo-Zufallszahlengenerators, der ein zufälliges Merkmal zur Aktualisierung auswählt. Wird verwendet, wenn ``selection`` == 'random'. Geben Sie eine ganze Zahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe an. Siehe :term:`Glossar `.	None
	selection selection: {'cyclic', 'random'}, Standardwert='cyclic' Wenn auf 'random' gesetzt, wird ein zufälliger Koeffizient in jeder Iteration aktualisiert anstatt standardmäßig sequenziell über die Merkmale zu iterieren. Dies (das Setzen auf 'random') führt oft zu einer deutlich schnelleren Konvergenz, insbesondere wenn tol höher als 1e-4 ist.	'cyclic'

	steps steps: list of tuples Liste von Tupeln (Name des Schritts, Schätzer), die in sequenzieller Reihenfolge verkettet werden sollen. Um mit der scikit-learn API kompatibel zu sein, müssen alle Schritte `fit` definieren. Alle nicht letzten Schritte müssen auch `transform` definieren. Siehe :ref:`Kombination von Schätzern ` für weitere Details.	[('columntransformer', ...), ('randomforestregressor', ...)]
	transform_input transform_input: list of str, default=None Die Namen der :term:`Metadaten`-Parameter, die von der Pipeline transformiert werden sollen, bevor sie an den Schritt übergeben werden, der sie benötigt. Dies ermöglicht die Transformation einiger Eingabeparameter zu ``fit`` (außer ``X``), die von den Schritten der Pipeline bis zu dem Schritt transformiert werden, der sie benötigt. Die Anforderung wird über :ref:`Metadaten-Routing ` definiert. Dies kann beispielsweise verwendet werden, um einen Validierungsdatensatz durch die Pipeline zu leiten. Sie können dies nur festlegen, wenn das Metadaten-Routing aktiviert ist, was Sie mit ``sklearn.set_config(enable_metadata_routing=True)`` aktivieren können. .. versionadded:: 1.6	None
	memory memory: str oder Objekt mit der joblib.Memory-Schnittstelle, default=None Wird zum Zwischenspeichern der angepassten Transformer der Pipeline verwendet. Der letzte Schritt wird niemals zwischengespeichert, auch wenn es sich um einen Transformer handelt. Standardmäßig erfolgt keine Zwischenspeicherung. Wenn ein String angegeben wird, ist dies der Pfad zum Zwischenspeicherverzeichnis. Durch Aktivieren der Zwischenspeicherung wird eine Kopie der Transformer vor dem Anpassen ausgelöst. Daher kann die an die Pipeline übergebene Transformer-Instanz nicht direkt inspiziert werden. Verwenden Sie das Attribut `named_steps` oder `steps`, um Schätzer innerhalb der Pipeline zu inspizieren. Das Zwischenspeichern der Transformer ist vorteilhaft, wenn das Anpassen zeitaufwändig ist. Siehe :ref:`sphx_glr_auto_examples_neighbors_plot_caching_nearest_neighbors.py` für ein Beispiel zur Aktivierung der Zwischenspeicherung.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Schritts gedruckt, wenn es abgeschlossen ist.	False

	n_estimators n_estimators: int, default=100 Die Anzahl der Bäume im Wald. .. versionchanged:: 0.22 Der Standardwert von ``n_estimators`` hat sich von 10 auf 100 in 0.22 geändert.	100
	criterion criterion: {"squared_error", "absolute_error", "friedman_mse", "poisson"}, Standardwert="squared_error" Die Funktion zur Messung der Qualität eines Splits. Unterstützte Kriterien sind "squared_error" für den mittleren quadratischen Fehler, der der Varianzreduktion als Kriterium zur Merkmalsauswahl entspricht und den L2- Verlust minimiert, indem der Mittelwert jedes Endknotens verwendet wird, "friedman_mse", der den mittleren quadratischen Fehler mit Friedmans Verbesserungs-Score für potenzielle Splits verwendet, "absolute_error" für den mittleren absoluten Fehler, der den L1-Verlust minimiert, indem der Median jedes Endknotens verwendet wird, und "poisson", der die Reduktion der Poisson-Devianz zur Ermittlung von Splits verwendet. Das Training mit "absolute_error" ist deutlich langsamer als bei Verwendung von "squared_error". .. versionadded:: 0.18 Kriterium für den mittleren absoluten Fehler (MAE). .. versionadded:: 1.0 Poisson-Kriterium.	'squared_error'
	max_depth max_depth: int, default=None Die maximale Tiefe des Baumes. Wenn None, werden Knoten erweitert, bis alle Blätter rein sind oder bis alle Blätter weniger als min_samples_split Stichproben enthalten.	None
	min_samples_split min_samples_split: int oder float, default=2 Die Mindestanzahl von Stichproben, die für einen internen Knoten zum Aufteilen erforderlich sind: - Wenn int, dann betrachten Sie `min_samples_split` als die Mindestanzahl. - Wenn float, dann ist `min_samples_split` ein Bruchteil und `ceil(min_samples_split * n_samples)` sind die Mindestanzahl von Stichproben für jeden Split. .. versionchanged:: 0.18 Hinzugefügte Gleitkommawerte für Brüche.	2
	min_samples_leaf min_samples_leaf: int oder float, default=1 Die Mindestanzahl von Stichproben, die an einem Blattknoten erforderlich sind. Ein Aufteilungspunkt in beliebiger Tiefe wird nur dann berücksichtigt, wenn er mindestens ``min_samples_leaf`` Trainingsstichproben in jedem der linken und rechten Zweige hinterlässt. Dies kann den Effekt haben, das Modell zu glätten, insbesondere bei der Regression. - Wenn int, dann betrachten Sie `min_samples_leaf` als die Mindestanzahl. - Wenn float, dann ist `min_samples_leaf` ein Bruchteil und `ceil(min_samples_leaf * n_samples)` sind die Mindestanzahl von Stichproben für jeden Knoten. .. versionchanged:: 0.18 Hinzugefügte Gleitkommawerte für Brüche.	1
	min_weight_fraction_leaf min_weight_fraction_leaf: float, Standard=0.0 Der minimale gewichtete Bruchteil der Gesamtsumme der Gewichte (aller Eingangsstichproben), der in einem Blattknoten erforderlich ist. Stichproben haben gleiches Gewicht, wenn sample_weight nicht angegeben ist.	0.0
	max_features max_features: {"sqrt", "log2", None}, int oder float, Standardwert=1.0 Die Anzahl der Merkmale, die bei der Suche nach dem besten Split berücksichtigt werden: - Wenn int, dann werden bei jedem Split `max_features` Merkmale berücksichtigt. - Wenn float, dann ist `max_features` ein Bruchteil und `max(1, int(max_features * n_features_in_))` Merkmale werden bei jedem Split berücksichtigt. - Wenn "sqrt", dann ist `max_features=sqrt(n_features)`. - Wenn "log2", dann ist `max_features=log2(n_features)`. - Wenn None oder 1.0, dann ist `max_features=n_features`. .. note:: Der Standardwert von 1.0 ist äquivalent zu Bagging-Bäumen und mehr Zufälligkeit kann durch kleinere Werte wie 0,3 erreicht werden. .. versionchanged:: 1.1 Der Standardwert von `max_features` änderte sich von `"auto"` zu 1.0. Hinweis: Die Suche nach einem Split stoppt nicht, bis mindestens eine gültige Partition der Knotenbeispiele gefunden wurde, auch wenn dies effektiv mehr als ``max_features`` Merkmale inspizieren erfordert.	1.0
	max_leaf_nodes max_leaf_nodes: int, Standard=None Wächst Bäume mit ``max_leaf_nodes`` im Best-First-Verfahren. Beste Knoten werden als relative Reduktion der Unreinheit definiert. Wenn None, dann unbegrenzte Anzahl von Blattknoten.	None
	min_impurity_decrease min_impurity_decrease: float, Standard=0.0 Ein Knoten wird geteilt, wenn diese Teilung eine Verringerung der Unreinheit von größer oder gleich diesem Wert bewirkt. Die Gleichung für die gewichtete Verringerung der Unreinheit lautet: N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity) wobei ``N`` die Gesamtzahl der Stichproben, ``N_t`` die Anzahl der Stichproben am aktuellen Knoten, ``N_t_L`` die Anzahl der Stichproben im linken Kind und ``N_t_R`` die Anzahl der Stichproben im rechten Kind ist. ``N``, ``N_t``, ``N_t_R`` und ``N_t_L`` beziehen sich alle auf die gewichtete Summe, wenn ``sample_weight`` übergeben wird. .. versionadded:: 0.19	0.0
	bootstrap bootstrap: bool, default=True Ob Bootstrap-Stichproben beim Aufbau von Bäumen verwendet werden. Wenn False, wird der gesamte Datensatz zum Aufbau jedes Baumes verwendet.	True
	oob_score oob_score: bool oder callable, Standardwert=False Ob Out-of-Bag-Stichproben zur Schätzung des Generalisierungs-Scores verwendet werden sollen. Standardmäßig wird :func:`~sklearn.metrics.r2_score` verwendet. Stellen Sie ein Callable mit der Signatur `metric(y_true, y_pred)` bereit, um eine benutzerdefinierte Metrik zu verwenden. Nur verfügbar, wenn `bootstrap=True`. Zur Veranschaulichung der Out-of-Bag (OOB)-Fehlerschätzung siehe das Beispiel :ref:`sphx_glr_auto_examples_ensemble_plot_ensemble_oob.py`.	False
	n_jobs n_jobs: int, default=None Die Anzahl der parallel auszuführenden Jobs. :meth:`fit`, :meth:`predict`, :meth:`decision_path` und :meth:`apply` werden alle parallel über die Bäume ausgeführt. ``None`` bedeutet 1, es sei denn, Sie befinden sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet die Verwendung aller Prozessoren. Siehe :term:`Glossary ` für weitere Details.	None
	random_state random_state: int, RandomState-Instanz oder None, default=None Steuert sowohl die Zufälligkeit des Bootstrapping der Stichproben, die beim Aufbau von Bäumen verwendet werden (wenn ``bootstrap=True``), als auch die Stichprobenziehung der Merkmale, die bei der Suche nach dem besten Split in jedem Knoten berücksichtigt werden (wenn ``max_features < n_features``). Siehe :term:`Glossary ` für Details.	42
	verbose verbose: int, Standard=0 Steuert die Ausführlichkeit beim Anpassen und Vorhersagen.	0
	warm_start warm_start: bool, Standard=False Wenn auf ``True`` gesetzt, wird die Lösung des vorherigen Aufrufs von fit wiederverwendet und weitere Estimators zum Ensemble hinzugefügt, andernfalls wird nur ein ganz neuer Wald angepasst. Siehe :term:`Glossary ` und :ref:`tree_ensemble_warm_start` für Details.	False
	ccp_alpha ccp_alpha: nicht-negative Gleitkommazahl, default=0.0 Komplexitätsparameter für Minimal Cost-Complexity Pruning. Der Teilbaum mit der größten Kostenkomplexität, die kleiner ist als ``ccp_alpha``, wird ausgewählt. Standardmäßig erfolgt kein Pruning. Siehe :ref:`minimal_cost_complexity_pruning` für Details. Siehe :ref:`sphx_glr_auto_examples_tree_plot_cost_complexity_pruning.py` für ein Beispiel für ein solches Pruning. .. versionadded:: 0.22	0.0
	max_samples max_samples: int oder float, default=None Wenn bootstrap True ist, die Anzahl der Stichproben, die aus X gezogen werden, um jeden Basisschätzer zu trainieren. - Wenn None (Standard), dann werden `X.shape[0]` Stichproben gezogen. - Wenn int, dann werden `max_samples` Stichproben gezogen. - Wenn float, dann werden `max(round(n_samples * max_samples), 1)` Stichproben gezogen. Daher sollte `max_samples` im Intervall `(0.0, 1.0]` liegen. .. versionadded:: 0.22	None
	monotonic_cst monotonic_cst: array-like von int der Form (n_features,), Standardwert=None Zeigt die Monotonie-Beschränkung an, die für jedes Merkmal durchgesetzt werden soll. - 1: monoton steigend - 0: keine Beschränkung - -1: monoton fallend Wenn monotonic_cst None ist, werden keine Beschränkungen angewendet. Monotonie-Beschränkungen werden nicht unterstützt für: - Mehrfachausgabe-Regressionen (d.h. wenn `n_outputs_ > 1`), - Regressionen, die auf Daten mit fehlenden Werten trainiert werden. Lesen Sie mehr im :ref:`Benutzerhandbuch `. .. versionadded:: 1.4	None

	steps steps: list of tuples Liste von Tupeln (Name des Schritts, Schätzer), die in sequenzieller Reihenfolge verkettet werden sollen. Um mit der scikit-learn API kompatibel zu sein, müssen alle Schritte `fit` definieren. Alle nicht letzten Schritte müssen auch `transform` definieren. Siehe :ref:`Kombination von Schätzern ` für weitere Details.	[('columntransformer', ...), ('histgradientboostingregressor', ...)]
	transform_input transform_input: list of str, default=None Die Namen der :term:`Metadaten`-Parameter, die von der Pipeline transformiert werden sollen, bevor sie an den Schritt übergeben werden, der sie benötigt. Dies ermöglicht die Transformation einiger Eingabeparameter zu ``fit`` (außer ``X``), die von den Schritten der Pipeline bis zu dem Schritt transformiert werden, der sie benötigt. Die Anforderung wird über :ref:`Metadaten-Routing ` definiert. Dies kann beispielsweise verwendet werden, um einen Validierungsdatensatz durch die Pipeline zu leiten. Sie können dies nur festlegen, wenn das Metadaten-Routing aktiviert ist, was Sie mit ``sklearn.set_config(enable_metadata_routing=True)`` aktivieren können. .. versionadded:: 1.6	None
	memory memory: str oder Objekt mit der joblib.Memory-Schnittstelle, default=None Wird zum Zwischenspeichern der angepassten Transformer der Pipeline verwendet. Der letzte Schritt wird niemals zwischengespeichert, auch wenn es sich um einen Transformer handelt. Standardmäßig erfolgt keine Zwischenspeicherung. Wenn ein String angegeben wird, ist dies der Pfad zum Zwischenspeicherverzeichnis. Durch Aktivieren der Zwischenspeicherung wird eine Kopie der Transformer vor dem Anpassen ausgelöst. Daher kann die an die Pipeline übergebene Transformer-Instanz nicht direkt inspiziert werden. Verwenden Sie das Attribut `named_steps` oder `steps`, um Schätzer innerhalb der Pipeline zu inspizieren. Das Zwischenspeichern der Transformer ist vorteilhaft, wenn das Anpassen zeitaufwändig ist. Siehe :ref:`sphx_glr_auto_examples_neighbors_plot_caching_nearest_neighbors.py` für ein Beispiel zur Aktivierung der Zwischenspeicherung.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Schritts gedruckt, wenn es abgeschlossen ist.	False

	loss loss: {'squared_error', 'absolute_error', 'gamma', 'poisson', 'quantile'}, default='squared_error' Die Verlustfunktion, die im Boosting-Prozess verwendet wird. Beachten Sie, dass die "squared error", "gamma" und "poisson" Verluste tatsächlich "half least squares loss", "half gamma deviance" und "half poisson deviance" implementieren, um die Berechnung des Gradienten zu vereinfachen. Darüber hinaus verwenden die Verluste "gamma" und "poisson" intern einen Log-Link, "gamma" erfordert ``y > 0`` und "poisson" erfordert ``y >= 0``. "quantile" verwendet den Pinball-Verlust. .. versionchanged:: 0.23 Option 'poisson' hinzugefügt. .. versionchanged:: 1.1 Option 'quantile' hinzugefügt. .. versionchanged:: 1.3 Option 'gamma' hinzugefügt.	'squared_error'
	quantile quantile: float, default=None Wenn loss "quantile" ist, gibt dieser Parameter an, welches Quantil geschätzt werden soll, und muss zwischen 0 und 1 liegen.	None
	learning_rate learning_rate: float, default=0.1 Die Lernrate, auch bekannt als Shrinkage. Sie wird als multiplikativer Faktor für die Blattwerte verwendet. Verwenden Sie ``1`` für keine Schrumpfung.	0.1
	max_iter max_iter: int, default=100 Die maximale Anzahl von Iterationen des Boosting-Prozesses, d.h. die maximale Anzahl von Bäumen.	100
	max_leaf_nodes max_leaf_nodes: int oder None, default=31 Die maximale Anzahl von Blättern pro Baum. Muss strikt größer als 1 sein. Wenn None, gibt es keine maximale Grenze.	31
	max_depth max_depth: int oder None, default=None Die maximale Tiefe jedes Baumes. Die Tiefe eines Baumes ist die Anzahl der Kanten, die vom Wurzelknoten zum tiefsten Blatt führen. Die Tiefe ist standardmäßig nicht begrenzt.	None
	min_samples_leaf min_samples_leaf: int, default=20 Die Mindestanzahl von Samples pro Blatt. Bei kleinen Datensätzen mit weniger als einigen hundert Samples wird empfohlen, diesen Wert zu senken, da nur sehr flache Bäume gebaut würden.	20
	l2_regularization l2_regularization: float, default=0 Der L2-Regularisierungsparameter, der Blätter mit kleinen Hessianen bestraft. Verwenden Sie ``0`` für keine Regularisierung (Standard).	0.0
	max_features max_features: float, default=1.0 Anteil zufällig ausgewählter Merkmale in jedem Knoten-Split. Dies ist eine Form der Regularisierung, kleinere Werte machen die Bäume zu schwächeren Lernern und können Überanpassung verhindern. Wenn Interaktionsbeschränkungen aus `interaction_cst` vorhanden sind, werden nur erlaubte Merkmale für die Unterstichprobe berücksichtigt. .. versionadded:: 1.4	1.0
	max_bins max_bins: int, default=255 Die maximale Anzahl von Bins, die für nicht fehlende Werte verwendet werden sollen. Vor dem Training wird jedes Merkmal des Eingabearrays `X` in ganzzahlige Bins eingeteilt, was eine viel schnellere Trainingsphase ermöglicht. Merkmale mit einer kleinen Anzahl von eindeutigen Werten verwenden möglicherweise weniger als ``max_bins`` Bins. Zusätzlich zu den ``max_bins`` Bins ist immer ein weiterer Bin für fehlende Werte reserviert. Muss nicht größer als 255 sein.	255
	categorical_features categorical_features: array-like von {bool, int, str} der Form (n_features) oder der Form (n_categorical_features,), Standardwert='from_dtype' Gibt die kategorialen Merkmale an. - None : kein Merkmal wird als kategorial betrachtet. - bool-Array-ähnlich : boolsche Maske, die kategoriale Merkmale angibt. - Ganzzahl-Array-ähnlich : Ganzzahl-Indizes, die kategoriale Merkmale angeben. - str-Array-ähnlich: Namen von kategorialen Merkmalen (vorausgesetzt, die Trainingsdaten haben Merkmalnamen). - `"from_dtype"`: DataFrame-Spalten mit dtype "category" werden als kategoriale Merkmale betrachtet. Die Eingabe muss ein Objekt sein, das eine ``__dataframe__``-Methode bereitstellt, wie z.B. pandas oder polars DataFrames, um dieses Feature zu nutzen. Für jedes kategoriale Merkmal darf es höchstens `max_bins` eindeutige Kategorien geben. Negative Werte für kategoriale Merkmale, die als numerische Datentypen kodiert sind, werden als fehlende Werte behandelt. Alle kategorialen Werte werden in Gleitkommazahlen umgewandelt. Das bedeutet, dass die kategorialen Werte 1.0 und 1 als dieselbe Kategorie behandelt werden. Lesen Sie mehr im :ref:`Benutzerhandbuch ` und :ref:`sphx_glr_auto_examples_ensemble_plot_gradient_boosting_categorical.py`. .. versionadded:: 0.24 .. versionchanged:: 1.2 Unterstützung für Merkmalnamen hinzugefügt. .. versionchanged:: 1.4 Option `"from_dtype"` hinzugefügt. .. versionchanged:: 1.6 Der Standardwert änderte sich von `None` zu `"from_dtype"`.	'from_dtype'
	monotonic_cst monotonic_cst: array-ähnlich von int mit shape (n_features) oder dict, default=None Monotone Einschränkungen, die für jedes Merkmal durchgesetzt werden sollen, werden mit den folgenden Integer-Werten angegeben: - 1: monoton steigend - 0: keine Einschränkung - -1: monoton fallend Wenn ein Dict mit String-Schlüsseln, ordnet es Merkmale zu monotonen Einschränkungen nach Namen zu. Wenn ein Array, werden die Merkmale Einschränkungen nach Position zugeordnet. Siehe :ref:`monotonic_cst_features_names` für ein Anwendungsbeispiel. Weiterlesen im :ref:`Benutzerhandbuch `. .. versionadded:: 0.23 .. versionchanged:: 1.2 Akzeptiert Dict von Einschränkungen mit Merkmalnamen als Schlüssel.	None
	interaction_cst interaction_cst: {"pairwise", "no_interactions"} oder Sequenz von Listen/Tupeln/Sets von int, Standardwert=None Spezifiziert Interaktionsbeschränkungen, die Mengen von Merkmalen, die sich gegenseitig in Kindknotensplits interagieren können. Jedes Element spezifiziert die Menge der Merkmalindizes, die miteinander interagieren dürfen. Wenn es mehr Merkmale gibt als in diesen Beschränkungen spezifiziert sind, werden sie so behandelt, als wären sie als zusätzliche Menge spezifiziert. Die Zeichenketten "pairwise" und "no_interactions" sind Kurzformen für die Erlaubnis von nur paarweisen oder gar keiner Interaktion. Zum Beispiel ist bei insgesamt 5 Merkmalen `interaction_cst=[{0, 1}]` äquivalent zu `interaction_cst=[{0, 1}, {2, 3, 4}]`, und spezifiziert, dass jeder Zweig eines Baumes entweder nur auf den Merkmalen 0 und 1 oder nur auf den Merkmalen 2, 3 und 4 splittet. Sehen Sie sich :ref:`dieses Beispiel` an, wie `interaction_cst` verwendet wird. .. versionadded:: 1.2	None
	warm_start warm_start: bool, default=False Wenn ``True`` gesetzt, wird die Lösung des vorherigen fit-Aufrufs wiederverwendet und weitere Schätzer zum Ensemble hinzugefügt. Damit die Ergebnisse gültig sind, sollte der Schätzer nur auf denselben Daten neu trainiert werden. Siehe :term:`Glossar `.	False
	early_stopping early_stopping: 'auto' oder bool, default='auto' Wenn 'auto', ist Early Stopping aktiviert, wenn die Stichprobengröße größer als 10000 ist oder wenn `X_val` und `y_val` an `fit` übergeben werden. Wenn True, ist Early Stopping aktiviert, andernfalls ist Early Stopping deaktiviert. .. versionadded:: 0.23	'auto'
	scoring scoring: str oder callable oder None, default='loss' Scoring-Methode, die für Early Stopping verwendet wird. Wird nur verwendet, wenn `early_stopping` aktiviert ist. Optionen: - str: siehe :ref:`scoring_string_names` für Optionen. - callable: ein Scorer-Callable-Objekt (z.B. Funktion) mit der Signatur ``scorer(estimator, X, y)``. Siehe :ref:`scoring_callable` für Details. - `None`: der :ref:`Bestimmtheitskoeffizient ` (:math:`R^2`) wird verwendet. - 'loss': Early Stopping wird im Vergleich zum Verlustwert überprüft.	'loss'
	validation_fraction validation_fraction: int oder float oder None, default=0.1 Anteil (oder absolute Größe) der Trainingsdaten, der als Validierungsdaten für Early Stopping zurückgestellt wird. Wenn None, erfolgt Early Stopping auf den Trainingsdaten. Der Wert wird ignoriert, wenn entweder kein Early Stopping durchgeführt wird (z.B. `early_stopping=False`) oder wenn `X_val` und `y_val` an fit übergeben werden.	0.1
	n_iter_no_change n_iter_no_change: int, default=10 Wird verwendet, um zu bestimmen, wann "Early Stop" erfolgen soll. Der Anpassungsprozess wird gestoppt, wenn keiner der letzten ``n_iter_no_change`` Scores besser ist als der ``n_iter_no_change - 1``-te-letzte, bis zu einer gewissen Toleranz. Nur verwendet, wenn Early Stopping durchgeführt wird.	10
	tol tol: float, default=1e-7 Die absolute Toleranz, die beim Vergleichen von Scores während des Early Stoppings verwendet wird. Je höher die Toleranz, desto wahrscheinlicher ist es, dass ein frühes Stoppen erfolgt: eine höhere Toleranz bedeutet, dass es für nachfolgende Iterationen schwieriger ist, als Verbesserung gegenüber dem Referenz-Score zu gelten.	1e-07
	verbose verbose: int, default=0 Die Ausführlichkeitsstufe. Wenn nicht null, werden einige Informationen über den Anpassungsprozess ausgegeben. ``1`` gibt nur eine Zusammenfassung aus, ``2`` gibt Informationen pro Iteration aus.	0
	random_state random_state: int, RandomState-Instanz oder None, default=None Pseudozufallszahlengenerator zur Steuerung der Unterabtastung im Binning-Prozess und der Trainings-/Validierungsdatensatzaufteilung, wenn Early Stopping aktiviert ist. Geben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe an. Siehe :term:`Glossar `.	0

	estimators estimators: list of (str, estimator) Basis-Estimators, die zusammen gestapelt werden. Jedes Element der Liste ist definiert als ein Tupel aus einer Zeichenkette (d.h. Name) und einer Estimator-Instanz. Ein Estimator kann mit `set_params` auf 'drop' gesetzt werden.	[('Random Forest', ...), ('Lasso', ...), ...]
	final_estimator final_estimator: estimator, Standardwert=None Ein Regressor, der zur Kombination der Basis-Estimators verwendet wird. Der Standard-Regressor ist ein :class:`~sklearn.linear_model.RidgeCV`.	RidgeCV()
	cv cv: int, Kreuzvalidierungsgenerator, iterierbar oder "prefit", Standardwert=None Bestimmt die Strategie der Kreuzvalidierungsteilung, die in `cross_val_predict` zum Trainieren von `final_estimator` verwendet wird. Mögliche Eingaben für cv sind: * None, um die standardmäßige 5-fache Kreuzvalidierung zu verwenden, * ganze Zahl, um die Anzahl der Folds in einem (geschichteten) KFold anzugeben, * Ein Objekt, das als Kreuzvalidierungsgenerator verwendet wird, * Ein iterierbares Objekt, das Trainings-, Test-Splits liefert, * `"prefit"`, um anzunehmen, dass die `estimators` vorab angepasst wurden. In diesem Fall werden die Estimators nicht erneut angepasst. Für ganzzahlige/None-Eingaben wird, wenn der Estimator ein Klassifikator ist und y entweder binär oder mehrklassig ist, :class:`~sklearn.model_selection.StratifiedKFold` verwendet. In allen anderen Fällen wird :class:`~sklearn.model_selection.KFold` verwendet. Diese Splitter werden mit `shuffle=False` instanziiert, sodass die Splits bei aufeinanderfolgenden Aufrufen gleich bleiben. Siehe das :ref:`Benutzerhandbuch ` für die verschiedenen Kreuzvalidierungsstrategien, die hier verwendet werden können. Wenn "prefit" übergeben wird, wird angenommen, dass alle `estimators` bereits angepasst wurden. Der `final_estimator_` wird auf den Vorhersagen der `estimators` auf dem vollständigen Trainingssatz trainiert und diese Vorhersagen sind nicht Kreuz-validiert. Bitte beachten Sie, dass bei gleicher Datenmenge zum Trainieren des Stacking-Modells ein sehr hohes Risiko von Overfitting besteht. .. versionadded:: 1.1 Die Option 'prefit' wurde in 1.1 hinzugefügt. .. note:: Eine größere Anzahl von Splits bringt keine Vorteile, wenn die Anzahl der Trainingsstichproben ausreichend groß ist. Tatsächlich erhöht sich die Trainingszeit. ``cv`` wird nicht zur Modellevaluierung, sondern zur Vorhersage verwendet.	None
	n_jobs n_jobs: int, Standardwert=None Die Anzahl der Jobs, die parallel für `fit` aller `estimators` ausgeführt werden. `None` bedeutet 1, es sei denn, Sie befinden sich in einem `joblib.parallel_backend`-Kontext. -1 bedeutet die Verwendung aller Prozessoren. Siehe :term:`Glossar ` für weitere Details.	None
	passthrough passthrough: bool, Standardwert=False Wenn False, werden nur die Vorhersagen der Estimators als Trainingsdaten für `final_estimator` verwendet. Wenn True, wird `final_estimator` sowohl auf den Vorhersagen als auch auf den Original-Trainingsdaten trainiert.	False
	verbose verbose: int, Standardwert=0 Umfang der Ausführlichkeit.	0

	alphas alphas: array-like der Form (n_alphas,), Standardwert=(0.1, 1.0, 10.0) Array von zu versuchenden Alpha-Werten. Regularisierungsstärke; muss eine positive Gleitkommazahl sein. Regularisierung verbessert die Konditionierung des Problems und reduziert die Varianz der Schätzungen. Größere Werte deuten auf eine stärkere Regularisierung hin. Alpha entspricht ``1 / (2C)`` in anderen linearen Modellen wie :class:`~sklearn.linear_model.LogisticRegression` oder :class:`~sklearn.svm.LinearSVC`. Bei Verwendung von Leave-One-Out-Kreuzvalidierung müssen Alphas strikt positiv sein.	(0.1, ...)
	fit_intercept fit_intercept: bool, Standardwert=True Ob der Achsenabschnitt für dieses Modell berechnet werden soll. Wenn auf False gesetzt, wird kein Achsenabschnitt bei den Berechnungen verwendet (d.h. die Daten werden als zentriert erwartet).	True
	scoring scoring: str, callable, Standardwert=None Die für die Kreuzvalidierung zu verwendende Scoring-Methode. Optionen: - str: siehe :ref:`scoring_string_names` für Optionen. - callable: ein Scorer-Callable-Objekt (z.B. Funktion) mit der Signatur ``scorer(estimator, X, y)``. Siehe :ref:`scoring_callable` für Details. - `None`: negativer :ref:`mittlerer quadratischer Fehler `, wenn cv None ist (d.h. bei Verwendung von Leave-One-Out-Kreuzvalidierung), oder :ref:`Bestimmungskoeffizient ` (:math:`R^2`) andernfalls.	None
	cv cv: int, Kreuzvalidierungsgenerator oder ein iterierbar, Standardwert=None Bestimmt die Strategie der Kreuzvalidierungsteilung. Mögliche Eingaben für cv sind: - None, um die effiziente Leave-One-Out-Kreuzvalidierung zu verwenden - ganze Zahl, um die Anzahl der Folds anzugeben. - :term:`CV-Teiler`, - Ein iterierbares Objekt, das (train, test) Splits als Array von Indizes liefert. Für ganzzahlige/None-Eingaben wird, wenn ``y`` binär oder mehrklassig ist, :class:`~sklearn.model_selection.StratifiedKFold` verwendet, andernfalls :class:`~sklearn.model_selection.KFold`. Siehe das :ref:`Benutzerhandbuch ` für die verschiedenen Kreuzvalidierungsstrategien, die hier verwendet werden können.	None
	gcv_mode gcv_mode: {'auto', 'svd', 'eigen'}, Standardwert='auto' Flag, das angibt, welche Strategie bei der Durchführung der Leave-One-Out-Kreuzvalidierung verwendet werden soll. Optionen sind:: 'auto' : verwende 'svd', wenn n_samples > n_features, andernfalls verwende 'eigen' 'svd' : erzwinge die Verwendung der Singulärwertzerlegung von X, wenn X dicht ist, Eigenwertzerlegung von X^T.X, wenn X dünn ist. 'eigen' : erzwinge die Berechnung über die Eigenwertzerlegung von X.X^T Der Modus 'auto' ist der Standard und soll je nach Form der Trainingsdaten die günstigere Option auswählen.	None
	store_cv_results store_cv_results: bool, Standardwert=False Flag, das angibt, ob die Kreuzvalidierungswerte, die jedem Alpha entsprechen, im Attribut ``cv_results_`` (siehe unten) gespeichert werden sollen. Dieses Flag ist nur kompatibel mit ``cv=None`` (d.h. mit Leave-One-Out-Kreuzvalidierung). .. versionchanged:: 1.5 Der Parametername wurde von `store_cv_values` in `store_cv_results` geändert.	False
	alpha_per_target alpha_per_target: bool, Standardwert=False Flag, das angibt, ob der Alpha-Wert (aus der `alphas`-Parameterliste ausgewählt) für jedes Ziel separat (bei Mehrfachausgabe) optimiert werden soll (mehrere Vorhersageziele). Wenn auf `True` gesetzt, enthält nach dem Anpassen das Attribut `alpha_` einen Wert für jedes Ziel. Wenn auf `False` gesetzt, wird ein einzelnes Alpha für alle Ziele verwendet. .. versionadded:: 0.24	False