Eine Demo der K-Means-Clusterbildung auf den handschriftlichen Zifferndaten

In diesem Beispiel vergleichen wir die verschiedenen Initialisierungsstrategien für K-Means hinsichtlich Laufzeit und Qualität der Ergebnisse.

Da die Grundwahrheit hier bekannt ist, wenden wir auch verschiedene Cluster-Qualitätsmetriken an, um die Güte der Anpassung der Cluster-Labels an die Grundwahrheit zu beurteilen.

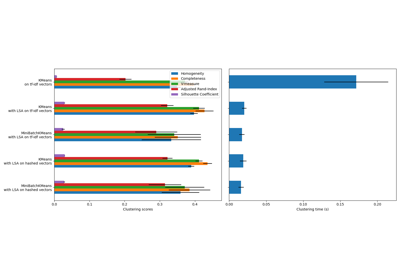
Ausgewertete Cluster-Qualitätsmetriken (Definitionen und Diskussionen der Metriken finden Sie unter Clustering-Leistungsbewertung)

Abkürzung	Voller Name
homo	Homogenitätswert
compl	Vollständigkeitswert
v-meas	V-Maß
ARI	angepasster Randindex
AMI	angepasste gegenseitige Information
silhouette	Silhouettenkoeffizient

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Laden des Datensatzes

Wir beginnen mit dem Laden des digits-Datensatzes. Dieser Datensatz enthält handschriftliche Ziffern von 0 bis 9. Im Kontext der Clusterbildung möchte man Bilder gruppieren, so dass die handschriftlichen Ziffern auf dem Bild gleich sind.

import numpy as np

from sklearn.datasets import load_digits

data, labels = load_digits(return_X_y=True)
(n_samples, n_features), n_digits = data.shape, np.unique(labels).size

print(f"# digits: {n_digits}; # samples: {n_samples}; # features {n_features}")

# digits: 10; # samples: 1797; # features 64

Definieren unseres Bewertungs-Benchmarks

Wir werden zunächst unseren Bewertungs-Benchmark erstellen. Während dieses Benchmarks beabsichtigen wir, verschiedene Initialisierungsmethoden für KMeans zu vergleichen. Unser Benchmark wird

• eine Pipeline erstellen, die die Daten mit einem StandardScaler skaliert;

• die Pipeline-Anpassung trainieren und zeitlich erfassen;

• die Leistung der Clusterbildung anhand verschiedener Metriken messen.

from time import time

from sklearn import metrics
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler


def bench_k_means(kmeans, name, data, labels):
    """Benchmark to evaluate the KMeans initialization methods.

    Parameters
    ----------
    kmeans : KMeans instance
        A :class:`~sklearn.cluster.KMeans` instance with the initialization
        already set.
    name : str
        Name given to the strategy. It will be used to show the results in a
        table.
    data : ndarray of shape (n_samples, n_features)
        The data to cluster.
    labels : ndarray of shape (n_samples,)
        The labels used to compute the clustering metrics which requires some
        supervision.
    """
    t0 = time()
    estimator = make_pipeline(StandardScaler(), kmeans).fit(data)
    fit_time = time() - t0
    results = [name, fit_time, estimator[-1].inertia_]

    # Define the metrics which require only the true labels and estimator
    # labels
    clustering_metrics = [
        metrics.homogeneity_score,
        metrics.completeness_score,
        metrics.v_measure_score,
        metrics.adjusted_rand_score,
        metrics.adjusted_mutual_info_score,
    ]
    results += [m(labels, estimator[-1].labels_) for m in clustering_metrics]

    # The silhouette score requires the full dataset
    results += [
        metrics.silhouette_score(
            data,
            estimator[-1].labels_,
            metric="euclidean",
            sample_size=300,
        )
    ]

    # Show the results
    formatter_result = (
        "{:9s}\t{:.3f}s\t{:.0f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}"
    )
    print(formatter_result.format(*results))

Ausführen des Benchmarks

Wir werden drei Ansätze vergleichen:

• eine Initialisierung mit k-means++. Diese Methode ist stochastisch und wir werden die Initialisierung 4 Mal ausführen;

• eine zufällige Initialisierung. Diese Methode ist ebenfalls stochastisch und wir werden die Initialisierung 4 Mal ausführen;

• eine Initialisierung basierend auf einer PCA-Projektion. Tatsächlich werden wir die Komponenten der PCA zur Initialisierung von KMeans verwenden. Diese Methode ist deterministisch und eine einzige Initialisierung reicht aus.

from sklearn.cluster import KMeans
from sklearn.decomposition import PCA

print(82 * "_")
print("init\t\ttime\tinertia\thomo\tcompl\tv-meas\tARI\tAMI\tsilhouette")

kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4, random_state=0)
bench_k_means(kmeans=kmeans, name="k-means++", data=data, labels=labels)

kmeans = KMeans(init="random", n_clusters=n_digits, n_init=4, random_state=0)
bench_k_means(kmeans=kmeans, name="random", data=data, labels=labels)

pca = PCA(n_components=n_digits).fit(data)
kmeans = KMeans(init=pca.components_, n_clusters=n_digits, n_init=1)
bench_k_means(kmeans=kmeans, name="PCA-based", data=data, labels=labels)

print(82 * "_")

__________________________________________________________________________________
init            time    inertia homo    compl   v-meas  ARI     AMI     silhouette
k-means++       0.033s  69545   0.598   0.645   0.621   0.469   0.617   0.158
random          0.038s  69735   0.681   0.723   0.701   0.574   0.698   0.173
PCA-based       0.014s  69513   0.600   0.647   0.622   0.468   0.618   0.162
__________________________________________________________________________________

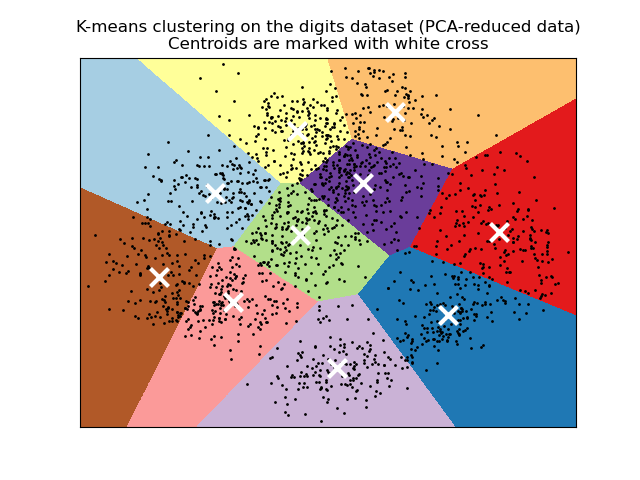
Visualisieren der Ergebnisse auf PCA-reduzierten Daten

PCA ermöglicht die Projektion der Daten aus dem ursprünglichen 64-dimensionalen Raum in einen niedrigerdimensionalen Raum. Anschließend können wir PCA verwenden, um in einen 2-dimensionalen Raum zu projizieren und die Daten und Cluster in diesem neuen Raum zu plotten.

import matplotlib.pyplot as plt

reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4)
kmeans.fit(reduced_data)

# Step size of the mesh. Decrease to increase the quality of the VQ.
h = 0.02  # point in the mesh [x_min, x_max]x[y_min, y_max].

# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(
    Z,
    interpolation="nearest",
    extent=(xx.min(), xx.max(), yy.min(), yy.max()),
    cmap=plt.cm.Paired,
    aspect="auto",
    origin="lower",
)

plt.plot(reduced_data[:, 0], reduced_data[:, 1], "k.", markersize=2)
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(
    centroids[:, 0],
    centroids[:, 1],
    marker="x",
    s=169,
    linewidths=3,
    color="w",
    zorder=10,
)
plt.title(
    "K-means clustering on the digits dataset (PCA-reduced data)\n"
    "Centroids are marked with white cross"
)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()

Verwandte Beispiele

Clustering von Textdokumenten mit K-Means

Clustering von Textdokumenten mit K-Means

Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

Empirische Auswertung des Einflusses der K-Means Initialisierung

Empirische Auswertung des Einflusses der K-Means Initialisierung

GMM Initialisierungsmethoden

GMM Initialisierungsmethoden