Gradient Boosting Regression

Dieses Beispiel demonstriert Gradient Boosting zur Erzeugung eines prädiktiven Modells aus einer Ensemble von schwachen prädiktiven Modellen. Gradient Boosting kann für Regressions- und Klassifizierungsprobleme verwendet werden. Hier trainieren wir ein Modell zur Bewältigung einer Diabetes-Regressionsaufgabe. Wir erhalten die Ergebnisse von GradientBoostingRegressor mit kleinsten Quadraten als Verlustfunktion und 500 Regressionsbäumen der Tiefe 4.

Hinweis: Für größere Datensätze (n_samples >= 10000) beachten Sie bitte HistGradientBoostingRegressor. Sehen Sie Merkmale in Histogramm-Gradient-Boosting-Bäumen für ein Beispiel, das einige weitere Vorteile von HistGradientBoostingRegressor zeigt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets, ensemble
from sklearn.inspection import permutation_importance
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.utils.fixes import parse_version

Daten laden

Zuerst müssen wir die Daten laden.

diabetes = datasets.load_diabetes()
X, y = diabetes.data, diabetes.target

Datenvorverarbeitung

Als Nächstes teilen wir unseren Datensatz auf, wobei 90 % für das Training verwendet werden und der Rest für Tests übrig bleibt. Wir werden auch die Parameter des Regressionsmodells festlegen. Sie können mit diesen Parametern experimentieren, um zu sehen, wie sich die Ergebnisse ändern.

n_estimators: Die Anzahl der durchzuführenden Boosting-Schritte. Später werden wir die Deviance gegen die Boosting-Iterationen plotten.

max_depth: Beschränkt die Anzahl der Knoten im Baum. Der beste Wert hängt von der Interaktion der Eingabevariablen ab.

min_samples_split: Die minimale Anzahl von Stichproben, die zum Aufteilen eines internen Knotens erforderlich sind.

learning_rate: Wie stark der Beitrag jedes Baumes geschrumpft wird.

loss: Zu optimierende Verlustfunktion. Die Funktion der kleinsten Quadrate wird in diesem Fall verwendet, es gibt jedoch viele andere Optionen (siehe GradientBoostingRegressor ).

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.1, random_state=13
)

params = {
    "n_estimators": 500,
    "max_depth": 4,
    "min_samples_split": 5,
    "learning_rate": 0.01,
    "loss": "squared_error",
}

Regressionsmodell anpassen

Nun initialisieren wir die Gradient-Boosting-Regressoren und passen sie an unsere Trainingsdaten an. Betrachten wir auch den mittleren quadratischen Fehler auf den Testdaten.

reg = ensemble.GradientBoostingRegressor(**params)
reg.fit(X_train, y_train)

mse = mean_squared_error(y_test, reg.predict(X_test))
print("The mean squared error (MSE) on test set: {:.4f}".format(mse))

The mean squared error (MSE) on test set: 3010.2061

Trainingsabweichung plotten

Schließlich visualisieren wir die Ergebnisse. Dazu berechnen wir zunächst die Testdatensatzabweichung und plotten sie dann gegen die Boosting-Iterationen.

test_score = np.zeros((params["n_estimators"],), dtype=np.float64)
for i, y_pred in enumerate(reg.staged_predict(X_test)):
    test_score[i] = mean_squared_error(y_test, y_pred)

fig = plt.figure(figsize=(6, 6))
plt.subplot(1, 1, 1)
plt.title("Deviance")
plt.plot(
    np.arange(params["n_estimators"]) + 1,
    reg.train_score_,
    "b-",
    label="Training Set Deviance",
)
plt.plot(
    np.arange(params["n_estimators"]) + 1, test_score, "r-", label="Test Set Deviance"
)
plt.legend(loc="upper right")
plt.xlabel("Boosting Iterations")
plt.ylabel("Deviance")
fig.tight_layout()
plt.show()

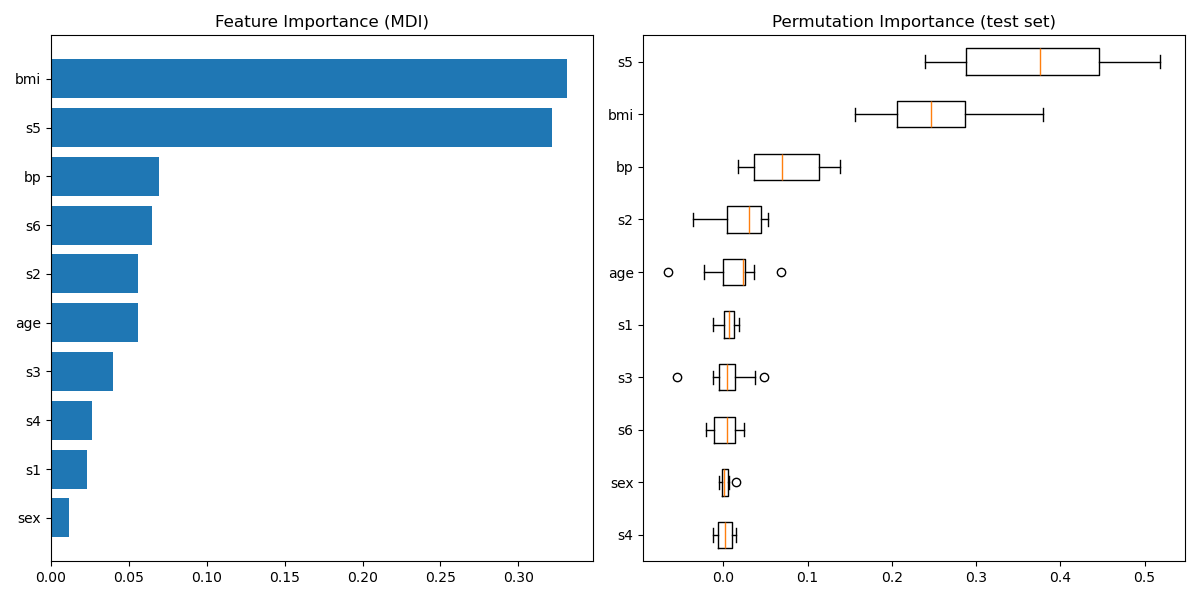
Merkmalswichtigkeit plotten

Warnung

Vorsicht, basierend auf der Verunreinigung berechnete Merkmalswichtigkeiten können irreführend sein für Merkmale mit **hoher Kardinalität** (viele eindeutige Werte). Alternativ können die Permutationswichtigkeiten von reg auf einem zurückgehaltenen Testdatensatz berechnet werden. Weitere Details finden Sie unter Permutations-Merkmalswichtigkeit.

Für dieses Beispiel identifizieren die auf Verunreinigung basierenden und die Permutationsmethoden dieselben 2 stark prädiktiven Merkmale, jedoch nicht in derselben Reihenfolge. Das drittwichtigste Merkmal, „bp“, ist für beide Methoden ebenfalls dasselbe. Die verbleibenden Merkmale sind weniger prädiktiv und die Fehlerbalken des Permutationsplots zeigen, dass sie mit 0 überlappen.

feature_importance = reg.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(pos, feature_importance[sorted_idx], align="center")
plt.yticks(pos, np.array(diabetes.feature_names)[sorted_idx])
plt.title("Feature Importance (MDI)")

result = permutation_importance(
    reg, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)

# `labels` argument in boxplot is deprecated in matplotlib 3.9 and has been
# renamed to `tick_labels`. The following code handles this, but as a
# scikit-learn user you probably can write simpler code by using `labels=...`
# (matplotlib < 3.9) or `tick_labels=...` (matplotlib >= 3.9).
tick_labels_parameter_name = (
    "tick_labels"
    if parse_version(matplotlib.__version__) >= parse_version("3.9")
    else "labels"
)
tick_labels_dict = {
    tick_labels_parameter_name: np.array(diabetes.feature_names)[sorted_idx]
}
plt.boxplot(result.importances[sorted_idx].T, vert=False, **tick_labels_dict)
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()

Verwandte Beispiele

Gradient Boosting Regularisierung

Gradient Boosting Regularisierung

Merkmalswichtigkeiten mit einem Wald von Bäumen

Merkmalswichtigkeiten mit einem Wald von Bäumen

Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen

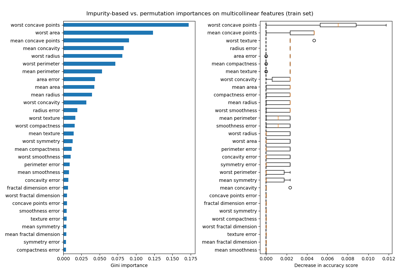
Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen