Hinweis
Zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder im Browser auszuführen.
Multi-class AdaBoosted Decision Trees#
Dieses Beispiel zeigt, wie Boosting die Vorhersagegenauigkeit bei einem Multi-Label-Klassifikationsproblem verbessern kann. Es reproduziert ein ähnliches Experiment wie in Abbildung 1 von Zhu et al. [1] dargestellt.
Das Kernprinzip von AdaBoost (Adaptive Boosting) besteht darin, eine Sequenz von schwachen Lernenden (z. B. Entscheidungsbäume) auf wiederholt neu abgetasteten Versionen der Daten anzupassen. Jede Stichprobe trägt ein Gewicht, das nach jedem Trainingsschritt angepasst wird, sodass falsch klassifizierte Stichproben höhere Gewichte erhalten. Der Stichprobenprozess mit Zurücklegen berücksichtigt die den einzelnen Stichproben zugewiesenen Gewichte. Stichproben mit höheren Gewichten haben eine größere Chance, mehrmals in der neuen Datensatz ausgewählt zu werden, während Stichproben mit niedrigeren Gewichten seltener ausgewählt werden. Dies stellt sicher, dass sich nachfolgende Iterationen des Algorithmus auf die schwer zu klassifizierenden Stichproben konzentrieren.
Referenzen
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Erstellung des Datensatzes#
Der Klassifikationsdatensatz wird konstruiert, indem eine zehn-dimensionale Standardnormalverteilung (\(x\) in \(R^{10}\)) genommen und drei Klassen definiert werden, die durch verschachtelte konzentrische zehn-dimensionale Kugeln getrennt sind, sodass ungefähr gleiche Anzahlen von Stichproben in jeder Klasse vorhanden sind (Quantile der \(\chi^2\)-Verteilung).
from sklearn.datasets import make_gaussian_quantiles
X, y = make_gaussian_quantiles(
n_samples=2_000, n_features=10, n_classes=3, random_state=1
)
Wir teilen den Datensatz in 2 Sätze auf: 70 Prozent der Stichproben werden für das Training und die restlichen 30 Prozent für das Testen verwendet.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, train_size=0.7, random_state=42
)
Training des AdaBoostClassifier#
Wir trainieren den AdaBoostClassifier. Der Schätzer nutzt Boosting, um die Klassifikationsgenauigkeit zu verbessern. Boosting ist eine Methode, die darauf abzielt, schwache Lernende (d. h. estimator) zu trainieren, die aus den Fehlern ihrer Vorgänger lernen.
Hier definieren wir den schwachen Lerner als DecisionTreeClassifier und setzen die maximale Anzahl von Blättern auf 8. In einer realen Situation sollte dieser Parameter angepasst werden. Wir setzen ihn auf einen eher niedrigen Wert, um die Laufzeit des Beispiels zu begrenzen.
Der in AdaBoostClassifier integrierte SAMME-Algorithmus verwendet dann die korrekten oder inkorrekten Vorhersagen des aktuellen schwachen Lernenden, um die Stichprobengewichte zu aktualisieren, die für das Training der nachfolgenden schwachen Lernenden verwendet werden. Außerdem wird das Gewicht des schwachen Lernenden selbst basierend auf seiner Genauigkeit bei der Klassifizierung der Trainingsbeispiele berechnet. Das Gewicht des schwachen Lernenden bestimmt seinen Einfluss auf die endgültige Ensemble-Vorhersage.
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
weak_learner = DecisionTreeClassifier(max_leaf_nodes=8)
n_estimators = 300
adaboost_clf = AdaBoostClassifier(
estimator=weak_learner,
n_estimators=n_estimators,
random_state=42,
).fit(X_train, y_train)
Analyse#
Konvergenz des AdaBoostClassifier#
Um die Effektivität von Boosting bei der Verbesserung der Genauigkeit zu demonstrieren, bewerten wir die Fehlklassifizierungsrate der geboosteten Bäume im Vergleich zu zwei Basiswerten. Der erste Basiswert ist die misclassification_error, die von einem einzelnen schwachen Lerner (d. h. einem DecisionTreeClassifier) erzielt wird und als Referenzpunkt dient. Der zweite Basiswert wird vom DummyClassifier erzielt, der die am häufigsten vorkommende Klasse in einem Datensatz vorhersagt.
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score
dummy_clf = DummyClassifier()
def misclassification_error(y_true, y_pred):
return 1 - accuracy_score(y_true, y_pred)
weak_learners_misclassification_error = misclassification_error(
y_test, weak_learner.fit(X_train, y_train).predict(X_test)
)
dummy_classifiers_misclassification_error = misclassification_error(
y_test, dummy_clf.fit(X_train, y_train).predict(X_test)
)
print(
"DecisionTreeClassifier's misclassification_error: "
f"{weak_learners_misclassification_error:.3f}"
)
print(
"DummyClassifier's misclassification_error: "
f"{dummy_classifiers_misclassification_error:.3f}"
)
DecisionTreeClassifier's misclassification_error: 0.475
DummyClassifier's misclassification_error: 0.692
Nach dem Training des DecisionTreeClassifier-Modells übersteigt der erreichte Fehler den erwarteten Wert, der durch Raten der häufigsten Klassenbezeichnung erzielt worden wäre, so wie es der DummyClassifier tut.
Nun berechnen wir die misclassification_error, d. h. 1 - accuracy, des additiven Modells (DecisionTreeClassifier) bei jeder Boosting-Iteration auf dem Testdatensatz, um seine Leistung zu bewerten.
Wir verwenden staged_predict, das so viele Iterationen wie Schätzer durchführt (d. h. entsprechend n_estimators). Bei Iteration n verwenden die Vorhersagen von AdaBoost nur die n ersten schwachen Lerner. Wir vergleichen diese Vorhersagen mit den tatsächlichen Vorhersagen y_test und schließen daraus auf den Nutzen (oder nicht) des Hinzufügens eines neuen schwachen Lerners in die Kette.
Wir plottieren die Fehlklassifizierungsrate für die verschiedenen Stufen
import matplotlib.pyplot as plt
import pandas as pd
boosting_errors = pd.DataFrame(
{
"Number of trees": range(1, n_estimators + 1),
"AdaBoost": [
misclassification_error(y_test, y_pred)
for y_pred in adaboost_clf.staged_predict(X_test)
],
}
).set_index("Number of trees")
ax = boosting_errors.plot()
ax.set_ylabel("Misclassification error on test set")
ax.set_title("Convergence of AdaBoost algorithm")
plt.plot(
[boosting_errors.index.min(), boosting_errors.index.max()],
[weak_learners_misclassification_error, weak_learners_misclassification_error],
color="tab:orange",
linestyle="dashed",
)
plt.plot(
[boosting_errors.index.min(), boosting_errors.index.max()],
[
dummy_classifiers_misclassification_error,
dummy_classifiers_misclassification_error,
],
color="c",
linestyle="dotted",
)
plt.legend(["AdaBoost", "DecisionTreeClassifier", "DummyClassifier"], loc=1)
plt.show()

Der Plot zeigt die Fehlklassifizierungsrate auf dem Testdatensatz nach jeder Boosting-Iteration. Wir sehen, dass die Fehlerrate der geboosteten Bäume nach 50 Iterationen zu einem Fehler von etwa 0,3 konvergiert, was eine signifikant höhere Genauigkeit im Vergleich zu einem einzelnen Baum darstellt, wie durch die gestrichelte Linie im Plot veranschaulicht.
Die Fehlklassifizierungsrate schwankt, da der SAMME-Algorithmus die diskreten Ausgaben der schwachen Lerner verwendet, um das geboostete Modell zu trainieren.
Die Konvergenz von AdaBoostClassifier wird hauptsächlich durch die Lernrate (d. h. learning_rate), die Anzahl der verwendeten schwachen Lerner (n_estimators) und die Ausdrucksstärke der schwachen Lerner (z. B. max_leaf_nodes) beeinflusst.
Fehler und Gewichte der schwachen Lerner#
Wie bereits erwähnt, ist AdaBoost ein vorwärts gerichtetes additives Modell. Wir konzentrieren uns nun darauf, die Beziehung zwischen den zugewiesenen Gewichten der schwachen Lerner und ihrer statistischen Leistung zu verstehen.
Wir verwenden die angepassten Attribute estimator_errors_ und estimator_weights_ des AdaBoostClassifier, um diesen Zusammenhang zu untersuchen.
weak_learners_info = pd.DataFrame(
{
"Number of trees": range(1, n_estimators + 1),
"Errors": adaboost_clf.estimator_errors_,
"Weights": adaboost_clf.estimator_weights_,
}
).set_index("Number of trees")
axs = weak_learners_info.plot(
subplots=True, layout=(1, 2), figsize=(10, 4), legend=False, color="tab:blue"
)
axs[0, 0].set_ylabel("Train error")
axs[0, 0].set_title("Weak learner's training error")
axs[0, 1].set_ylabel("Weight")
axs[0, 1].set_title("Weak learner's weight")
fig = axs[0, 0].get_figure()
fig.suptitle("Weak learner's errors and weights for the AdaBoostClassifier")
fig.tight_layout()
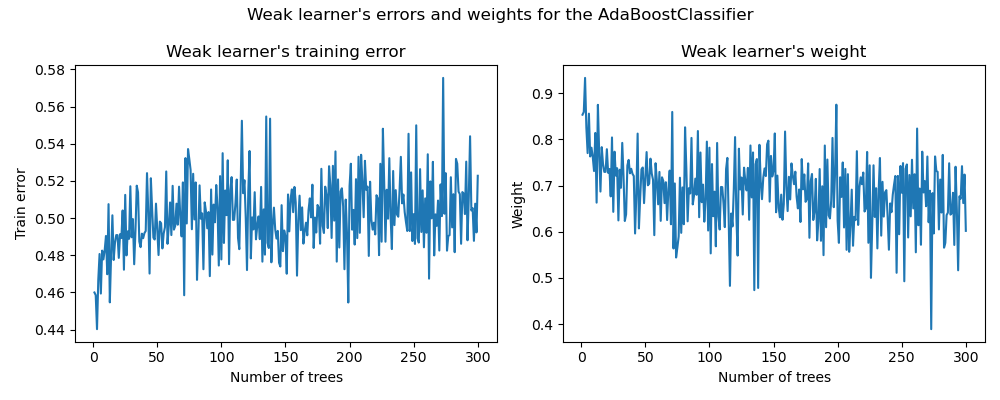
Auf der linken Seite des Plots zeigen wir den gewichteten Fehler jedes schwachen Lerners auf dem neu gewichteten Trainingsdatensatz in jeder Boosting-Iteration. Auf der rechten Seite des Plots zeigen wir die Gewichte, die jedem schwachen Lerner zugewiesen sind und später verwendet werden, um die Vorhersagen des endgültigen additiven Modells zu treffen.
Wir sehen, dass der Fehler des schwachen Lerners umgekehrt proportional zu den Gewichten ist. Das bedeutet, dass unser additives Modell einem schwachen Lerner, der kleinere Fehler macht (auf dem Trainingsdatensatz), mehr Vertrauen schenkt, indem es seinen Einfluss auf die endgültige Entscheidung erhöht. Dies ist tatsächlich genau die Formulierung der Aktualisierung der Gewichte der Basis-Schätzer nach jeder Iteration in AdaBoost.
Mathematische Details#
Das Gewicht, das einem schwachen Lerner zugeordnet ist, der in der Stufe \(m\) trainiert wurde, ist umgekehrt proportional zu seinem Fehlklassifizierungsfehler, so dass
wobei \(\alpha^{(m)}\) und \(\text{err}^{(m)}\) das Gewicht bzw. der Fehler des \(m\)-ten schwachen Lerners sind und \(K\) die Anzahl der Klassen in unserem Klassifikationsproblem ist.
Eine weitere interessante Beobachtung ist, dass die ersten schwachen Lerner des Modells weniger Fehler machen als spätere schwache Lerner der Boosting-Kette.
Die Intuition hinter dieser Beobachtung ist folgende: Aufgrund der Stichproben-Neugewichtung werden spätere Klassifikatoren gezwungen, schwierigere oder verrauschte Stichproben zu klassifizieren und bereits gut klassifizierte Stichproben zu ignorieren. Daher wird der Gesamtfehler auf dem Trainingsdatensatz zunehmen. Deshalb sind die Gewichte der schwachen Lerner so konstruiert, dass sie die schlechter abschneidenden schwachen Lerner ausgleichen.
Gesamtlaufzeit des Skripts: (0 Minuten 3,299 Sekunden)
Verwandte Beispiele
Entscheidungsflächen von Ensembles von Bäumen auf dem Iris-Datensatz plotten