Probabilistische Vorhersagen mit Gaußschen Prozessklassifikation (GPC)

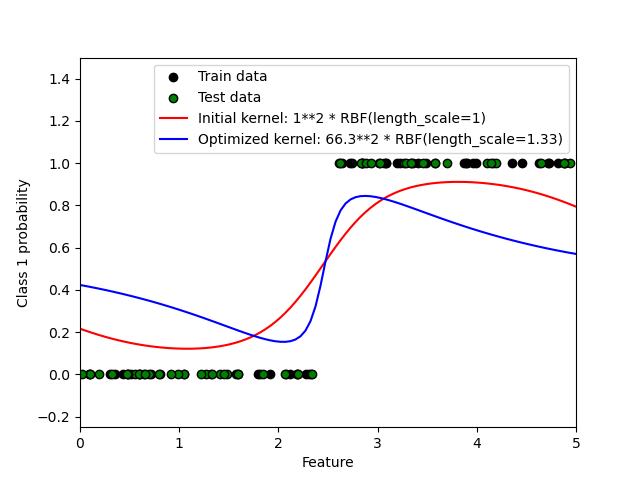
Dieses Beispiel illustriert die vorhergesagte Wahrscheinlichkeit von GPC für einen RBF-Kernel mit verschiedenen Wahlen der Hyperparameter. Die erste Abbildung zeigt die vorhergesagte Wahrscheinlichkeit von GPC mit willkürlich gewählten Hyperparametern und mit den Hyperparametern, die der maximalen Log-Marginal-Likelihood (LML) entsprechen.

Während die durch Optimierung der LML gewählten Hyperparameter eine erheblich größere LML aufweisen, schneiden sie gemäß dem Log-Loss auf Testdaten geringfügig schlechter ab. Die Abbildung zeigt, dass dies daran liegt, dass sie eine steile Änderung der Klassenwahrscheinlichkeiten an den Klassengrenzen aufweisen (was gut ist), aber vorhergesagte Wahrscheinlichkeiten nahe 0,5 weit von den Klassengrenzen entfernt haben (was schlecht ist). Dieser unerwünschte Effekt wird durch die Laplace-Approximation verursacht, die intern von GPC verwendet wird.

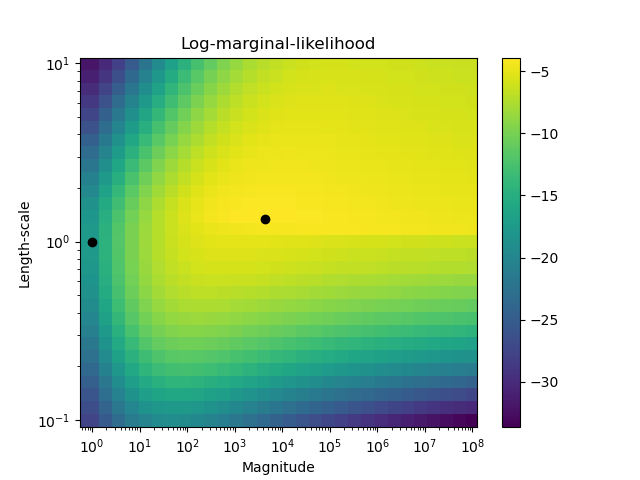
Die zweite Abbildung zeigt die Log-Marginal-Likelihood für verschiedene Wahlen der Hyperparameter des Kernels, wobei die beiden Wahlen der Hyperparameter aus der ersten Abbildung durch schwarze Punkte hervorgehoben werden.

• 
• 

Log Marginal Likelihood (initial): -17.598
Log Marginal Likelihood (optimized): -3.875
Accuracy: 1.000 (initial) 1.000 (optimized)
Log-loss: 0.214 (initial) 0.319 (optimized)

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import numpy as np
from matplotlib import pyplot as plt

from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, log_loss

# Generate data
train_size = 50
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 100)[:, np.newaxis]
y = np.array(X[:, 0] > 2.5, dtype=int)

# Specify Gaussian Processes with fixed and optimized hyperparameters
gp_fix = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0), optimizer=None)
gp_fix.fit(X[:train_size], y[:train_size])

gp_opt = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0))
gp_opt.fit(X[:train_size], y[:train_size])

print(
    "Log Marginal Likelihood (initial): %.3f"
    % gp_fix.log_marginal_likelihood(gp_fix.kernel_.theta)
)
print(
    "Log Marginal Likelihood (optimized): %.3f"
    % gp_opt.log_marginal_likelihood(gp_opt.kernel_.theta)
)

print(
    "Accuracy: %.3f (initial) %.3f (optimized)"
    % (
        accuracy_score(y[:train_size], gp_fix.predict(X[:train_size])),
        accuracy_score(y[:train_size], gp_opt.predict(X[:train_size])),
    )
)
print(
    "Log-loss: %.3f (initial) %.3f (optimized)"
    % (
        log_loss(y[:train_size], gp_fix.predict_proba(X[:train_size])[:, 1]),
        log_loss(y[:train_size], gp_opt.predict_proba(X[:train_size])[:, 1]),
    )
)


# Plot posteriors
plt.figure()
plt.scatter(
    X[:train_size, 0], y[:train_size], c="k", label="Train data", edgecolors=(0, 0, 0)
)
plt.scatter(
    X[train_size:, 0], y[train_size:], c="g", label="Test data", edgecolors=(0, 0, 0)
)
X_ = np.linspace(0, 5, 100)
plt.plot(
    X_,
    gp_fix.predict_proba(X_[:, np.newaxis])[:, 1],
    "r",
    label="Initial kernel: %s" % gp_fix.kernel_,
)
plt.plot(
    X_,
    gp_opt.predict_proba(X_[:, np.newaxis])[:, 1],
    "b",
    label="Optimized kernel: %s" % gp_opt.kernel_,
)
plt.xlabel("Feature")
plt.ylabel("Class 1 probability")
plt.xlim(0, 5)
plt.ylim(-0.25, 1.5)
plt.legend(loc="best")

# Plot LML landscape
plt.figure()
theta0 = np.logspace(0, 8, 30)
theta1 = np.logspace(-1, 1, 29)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [
    [
        gp_opt.log_marginal_likelihood(np.log([Theta0[i, j], Theta1[i, j]]))
        for i in range(Theta0.shape[0])
    ]
    for j in range(Theta0.shape[1])
]
LML = np.array(LML).T
plt.plot(
    np.exp(gp_fix.kernel_.theta)[0], np.exp(gp_fix.kernel_.theta)[1], "ko", zorder=10
)
plt.plot(
    np.exp(gp_opt.kernel_.theta)[0], np.exp(gp_opt.kernel_.theta)[1], "ko", zorder=10
)
plt.pcolor(Theta0, Theta1, LML)
plt.xscale("log")
plt.yscale("log")
plt.colorbar()
plt.xlabel("Magnitude")
plt.ylabel("Length-scale")
plt.title("Log-marginal-likelihood")

plt.show()

Verwandte Beispiele

Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels

Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels

Illustration der Gauß-Prozess-Klassifikation (GPC) auf dem XOR-Datensatz

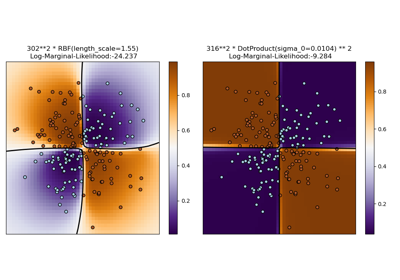
Illustration der Gauß-Prozess-Klassifikation (GPC) auf dem XOR-Datensatz

Skalierung des Regularisierungsparameters für SVCs

Skalierung des Regularisierungsparameters für SVCs

Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz

Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz