Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Robuste Kovarianzschätzung und die Relevanz von Mahalanobis-Distanzen#
Dieses Beispiel zeigt die Kovarianzschätzung mit Mahalanobis-Distanzen auf Gauß-verteilten Daten.
Für Gauß-verteilte Daten kann der Abstand einer Beobachtung \(x_i\) zum Modus der Verteilung mithilfe ihrer Mahalanobis-Distanz berechnet werden:
wobei \(\mu\) und \(\Sigma\) der Ort und die Kovarianz der zugrunde liegenden Gauß-Verteilungen sind.
In der Praxis werden \(\mu\) und \(\Sigma\) durch Schätzungen ersetzt. Die standardmäßige Kovarianzschätzung nach der Maximum-Likelihood-Methode (MLE) ist sehr empfindlich gegenüber Ausreißern im Datensatz, und daher sind auch die nachgeschalteten Mahalanobis-Distanzen empfindlich. Es wäre besser, einen robusten Kovarianzschätzer zu verwenden, um sicherzustellen, dass die Schätzung gegenüber „fehlerhaften“ Beobachtungen im Datensatz widerstandsfähig ist und dass die berechneten Mahalanobis-Distanzen die wahre Organisation der Beobachtungen genau widerspiegeln.
Der Minimum-Kovarianz-Determinanten-Schätzer (MCD) ist ein robuster Schätzer mit hohem Break-Down-Punkt (d.h. er kann verwendet werden, um die Kovarianzmatrix von stark kontaminierten Datensätzen zu schätzen, bis zu \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) Ausreißer). Die Idee hinter dem MCD ist es, \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) Beobachtungen zu finden, deren empirische Kovarianz die kleinste Determinante hat, was zu einer „reinen“ Teilmenge von Beobachtungen führt, aus der Standardschätzungen für Ort und Kovarianz berechnet werden können. Der MCD wurde von P.J.Rousseuw in [1] eingeführt.
Dieses Beispiel veranschaulicht, wie sich Mahalanobis-Distanzen durch Ausreißerdaten verändern. Beobachtungen, die aus einer kontaminierenden Verteilung stammen, sind von den Beobachtungen der echten, Gauß-Verteilung nicht zu unterscheiden, wenn standardmäßige, auf MLE basierende Mahalanobis-Distanzen verwendet werden. Mit MCD-basierten Mahalanobis-Distanzen werden die beiden Populationen unterscheidbar. Zugehörige Anwendungen umfassen die Ausreißererkennung, die Rangordnung von Beobachtungen und das Clustering.
Hinweis
Siehe auch Robuste vs. empirische Kovarianzschätzung
Referenzen
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Daten generieren#
Zuerst generieren wir einen Datensatz mit 125 Stichproben und 2 Merkmalen. Beide Merkmale sind Gauß-verteilt mit einem Mittelwert von 0, aber Merkmal 1 hat eine Standardabweichung von 2 und Merkmal 2 eine Standardabweichung von 1. Anschließend werden 25 Stichproben durch Gauß-Ausreißerstichproben ersetzt, bei denen Merkmal 1 eine Standardabweichung von 1 und Merkmal 2 eine Standardabweichung von 7 aufweist.
import numpy as np
# for consistent results
np.random.seed(7)
n_samples = 125
n_outliers = 25
n_features = 2
# generate Gaussian data of shape (125, 2)
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.0
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.0
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)
Vergleich der Ergebnisse#
Im Folgenden passen wir MCD- und MLE-basierte Kovarianzschätzer an unsere Daten an und geben die geschätzten Kovarianzmatrizen aus. Beachten Sie, dass die geschätzte Varianz von Merkmal 2 beim MLE-basierten Schätzer (7,5) viel höher ist als beim robusten MCD-Schätzer (1,2). Dies zeigt, dass der MCD-basierte robuste Schätzer gegenüber den Ausreißerstichproben, die so konzipiert wurden, dass sie eine viel größere Varianz in Merkmal 2 aufweisen, viel widerstandsfähiger ist.
import matplotlib.pyplot as plt
from sklearn.covariance import EmpiricalCovariance, MinCovDet
# fit a MCD robust estimator to data
robust_cov = MinCovDet().fit(X)
# fit a MLE estimator to data
emp_cov = EmpiricalCovariance().fit(X)
print(
"Estimated covariance matrix:\nMCD (Robust):\n{}\nMLE:\n{}".format(
robust_cov.covariance_, emp_cov.covariance_
)
)
Estimated covariance matrix:
MCD (Robust):
[[ 3.60075119 -0.07640781]
[-0.07640781 1.51855963]]
MLE:
[[ 3.23773583 -0.24640578]
[-0.24640578 7.51963999]]
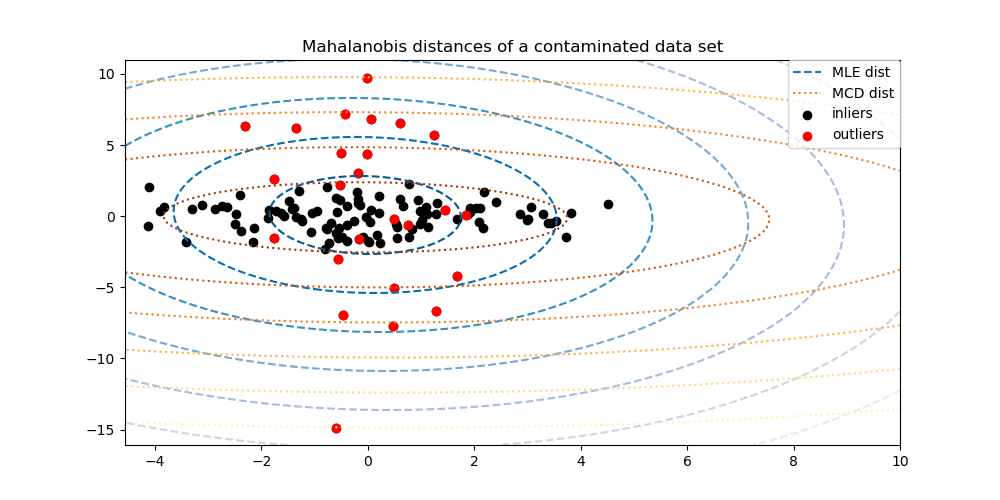
Um den Unterschied besser zu visualisieren, plotten wir Konturen der Mahalanobis-Distanzen, die von beiden Methoden berechnet wurden. Beachten Sie, dass die robusten MCD-basierten Mahalanobis-Distanzen die inneren schwarzen Punkte viel besser treffen, während die MLE-basierten Distanzen stärker von den äußeren roten Punkten beeinflusst werden.
import matplotlib.lines as mlines
fig, ax = plt.subplots(figsize=(10, 5))
# Plot data set
inlier_plot = ax.scatter(X[:, 0], X[:, 1], color="black", label="inliers")
outlier_plot = ax.scatter(
X[:, 0][-n_outliers:], X[:, 1][-n_outliers:], color="red", label="outliers"
)
ax.set_xlim(ax.get_xlim()[0], 10.0)
ax.set_title("Mahalanobis distances of a contaminated data set")
# Create meshgrid of feature 1 and feature 2 values
xx, yy = np.meshgrid(
np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
# Calculate the MLE based Mahalanobis distances of the meshgrid
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles="dashed"
)
# Calculate the MCD based Mahalanobis distances
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(
xx, yy, np.sqrt(mahal_robust_cov), cmap=plt.cm.YlOrBr_r, linestyles="dotted"
)
# Add legend
ax.legend(
[
mlines.Line2D([], [], color="tab:blue", linestyle="dashed"),
mlines.Line2D([], [], color="tab:orange", linestyle="dotted"),
inlier_plot,
outlier_plot,
],
["MLE dist", "MCD dist", "inliers", "outliers"],
loc="upper right",
borderaxespad=0,
)
plt.show()
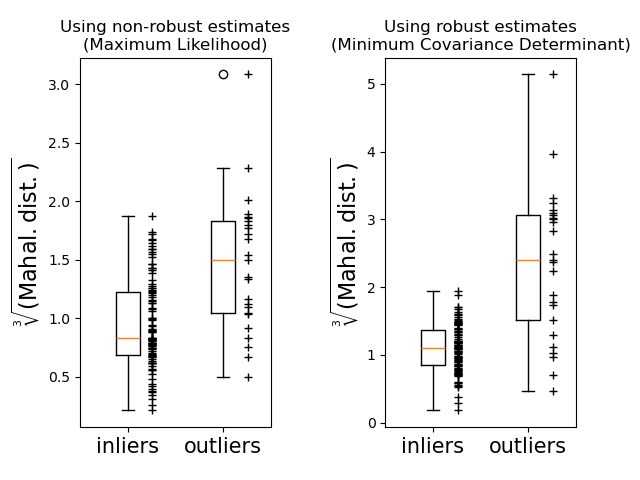
Schließlich heben wir die Fähigkeit von MCD-basierten Mahalanobis-Distanzen hervor, Ausreißer zu unterscheiden. Wir nehmen die Kubikwurzel der Mahalanobis-Distanzen, was annähernd normale Verteilungen ergibt (wie von Wilson und Hilferty vorgeschlagen [2]), und plotten dann die Werte der inneren und äußeren Stichproben mit Boxplots. Die Verteilung der Ausreißerstichproben ist bei robusten, MCD-basierten Mahalanobis-Distanzen stärker von der Verteilung der inneren Stichproben getrennt.
fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=0.6)
# Calculate cubic root of MLE Mahalanobis distances for samples
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# Plot boxplots
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax1.plot(
np.full(n_samples - n_outliers, 1.26),
emp_mahal[:-n_outliers],
"+k",
markeredgewidth=1,
)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax1.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("Using non-robust estimates\n(Maximum Likelihood)")
# Calculate cubic root of MCD Mahalanobis distances for samples
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# Plot boxplots
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax2.plot(
np.full(n_samples - n_outliers, 1.26),
robust_mahal[:-n_outliers],
"+k",
markeredgewidth=1,
)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax2.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("Using robust estimates\n(Minimum Covariance Determinant)")
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,228 Sekunden)
Verwandte Beispiele
Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen
Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid