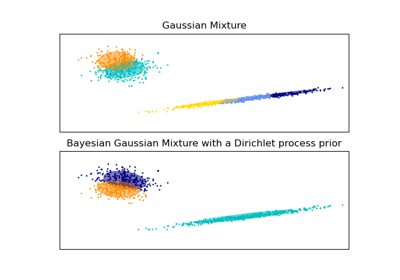
GMM-Kovarianzen

Demonstration verschiedener Kovarianztypen für Gaußsche Mischmodelle.

Weitere Informationen zum Estimator finden Sie unter Gaußsche Mischmodelle.

Obwohl GMMs häufig zum Clustering verwendet werden, können wir die erhaltenen Cluster mit den tatsächlichen Klassen aus dem Datensatz vergleichen. Wir initialisieren die Mittelwerte der Gaußschen Verteilungen mit den Mittelwerten der Klassen aus dem Trainingsdatensatz, um diesen Vergleich gültig zu machen.

Wir plotten vorhergesagte Labels sowohl auf Trainings- als auch auf zurückgehaltenen Testdaten unter Verwendung einer Vielzahl von GMM-Kovarianztypen auf dem Iris-Datensatz. Wir vergleichen GMMs mit sphärischen, diagonalen, vollständigen und gebundenen Kovarianzmatrizen in aufsteigender Reihenfolge der Leistung. Obwohl man erwarten würde, dass die vollständige Kovarianz im Allgemeinen am besten abschneidet, ist sie anfällig für Überanpassung bei kleinen Datensätzen und verallgemeinert sich nicht gut auf zurückgehaltene Testdaten.

Auf den Plots werden Trainingsdaten als Punkte und Testdaten als Kreuze dargestellt. Der Iris-Datensatz ist vierdimensional. Hier werden nur die ersten beiden Dimensionen gezeigt, und daher sind einige Punkte in anderen Dimensionen getrennt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold

colors = ["navy", "turquoise", "darkorange"]


def make_ellipses(gmm, ax):
    for n, color in enumerate(colors):
        if gmm.covariance_type == "full":
            covariances = gmm.covariances_[n][:2, :2]
        elif gmm.covariance_type == "tied":
            covariances = gmm.covariances_[:2, :2]
        elif gmm.covariance_type == "diag":
            covariances = np.diag(gmm.covariances_[n][:2])
        elif gmm.covariance_type == "spherical":
            covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
        v, w = np.linalg.eigh(covariances)
        u = w[0] / np.linalg.norm(w[0])
        angle = np.arctan2(u[1], u[0])
        angle = 180 * angle / np.pi  # convert to degrees
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        ell = mpl.patches.Ellipse(
            gmm.means_[n, :2], v[0], v[1], angle=180 + angle, color=color
        )
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(0.5)
        ax.add_artist(ell)
        ax.set_aspect("equal", "datalim")


iris = datasets.load_iris()

# Break up the dataset into non-overlapping training (75%) and testing
# (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))


X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]

n_classes = len(np.unique(y_train))

# Try GMMs using different types of covariances.
estimators = {
    cov_type: GaussianMixture(
        n_components=n_classes, covariance_type=cov_type, max_iter=20, random_state=0
    )
    for cov_type in ["spherical", "diag", "tied", "full"]
}

n_estimators = len(estimators)

plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(
    bottom=0.01, top=0.95, hspace=0.15, wspace=0.05, left=0.01, right=0.99
)


for index, (name, estimator) in enumerate(estimators.items()):
    # Since we have class labels for the training data, we can
    # initialize the GMM parameters in a supervised manner.
    estimator.means_init = np.array(
        [X_train[y_train == i].mean(axis=0) for i in range(n_classes)]
    )

    # Train the other parameters using the EM algorithm.
    estimator.fit(X_train)

    h = plt.subplot(2, n_estimators // 2, index + 1)
    make_ellipses(estimator, h)

    for n, color in enumerate(colors):
        data = iris.data[iris.target == n]
        plt.scatter(
            data[:, 0], data[:, 1], s=0.8, color=color, label=iris.target_names[n]
        )
    # Plot the test data with crosses
    for n, color in enumerate(colors):
        data = X_test[y_test == n]
        plt.scatter(data[:, 0], data[:, 1], marker="x", color=color)

    y_train_pred = estimator.predict(X_train)
    train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
    plt.text(0.05, 0.9, "Train accuracy: %.1f" % train_accuracy, transform=h.transAxes)

    y_test_pred = estimator.predict(X_test)
    test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
    plt.text(0.05, 0.8, "Test accuracy: %.1f" % test_accuracy, transform=h.transAxes)

    plt.xticks(())
    plt.yticks(())
    plt.title(name)

plt.legend(scatterpoints=1, loc="lower right", prop=dict(size=12))


plt.show()

Verwandte Beispiele

Gaußsche Mischmodell-Ellipsoide

Gaußsche Mischmodell-Ellipsoide

GMM Initialisierungsmethoden

GMM Initialisierungsmethoden

Gaußsche Mischmodell-Sinuskurve

Gaußsche Mischmodell-Sinuskurve

Gaußsche Mischmodell-Auswahl

Gaußsche Mischmodell-Auswahl