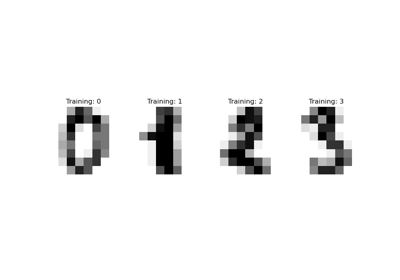Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Label Propagation Ziffern: Aktives Lernen#
Demonstriert eine Technik des aktiven Lernens zum Erlernen handschriftlicher Ziffern mittels Label Propagation.
Wir beginnen mit dem Training eines Label Propagation Modells mit nur 10 gelabelten Punkten, dann wählen wir die fünf unsichersten Punkte aus, um sie zu labeln. Anschließend trainieren wir mit 15 gelabelten Punkten (die ursprünglichen 10 + 5 neuen). Wir wiederholen diesen Vorgang viermal, um ein Modell zu erhalten, das mit 30 gelabelten Beispielen trainiert wurde. Beachten Sie, dass Sie dies erhöhen können, um mehr als 30 zu labeln, indem Sie max_iterations ändern. Das Labeln von mehr als 30 kann nützlich sein, um ein Gefühl für die Konvergenzgeschwindigkeit dieser Technik des aktiven Lernens zu bekommen.
Es wird ein Diagramm angezeigt, das die 5 unsichersten Ziffern für jede Trainingsiteration zeigt. Diese können Fehler enthalten oder auch nicht, aber wir werden das nächste Modell mit ihren wahren Labels trainieren.

Iteration 0 ______________________________________________________________________
Label Spreading model: 40 labeled & 290 unlabeled (330 total)
precision recall f1-score support
0 1.00 1.00 1.00 22
1 0.78 0.69 0.73 26
2 0.93 0.93 0.93 29
3 1.00 0.89 0.94 27
4 0.92 0.96 0.94 23
5 0.96 0.70 0.81 33
6 0.97 0.97 0.97 35
7 0.94 0.91 0.92 33
8 0.62 0.89 0.74 28
9 0.73 0.79 0.76 34
accuracy 0.87 290
macro avg 0.89 0.87 0.87 290
weighted avg 0.88 0.87 0.87 290
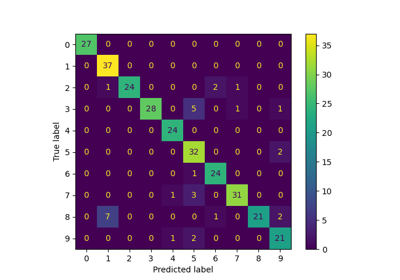
Confusion matrix
[[22 0 0 0 0 0 0 0 0 0]
[ 0 18 2 0 0 0 1 0 5 0]
[ 0 0 27 0 0 0 0 0 2 0]
[ 0 0 0 24 0 0 0 0 3 0]
[ 0 1 0 0 22 0 0 0 0 0]
[ 0 0 0 0 0 23 0 0 0 10]
[ 0 1 0 0 0 0 34 0 0 0]
[ 0 0 0 0 0 0 0 30 3 0]
[ 0 3 0 0 0 0 0 0 25 0]
[ 0 0 0 0 2 1 0 2 2 27]]
Iteration 1 ______________________________________________________________________
Label Spreading model: 45 labeled & 285 unlabeled (330 total)
precision recall f1-score support
0 1.00 1.00 1.00 22
1 0.79 1.00 0.88 22
2 1.00 0.93 0.96 29
3 1.00 1.00 1.00 26
4 0.92 0.96 0.94 23
5 0.96 0.70 0.81 33
6 1.00 0.97 0.99 35
7 0.94 0.91 0.92 33
8 0.77 0.86 0.81 28
9 0.73 0.79 0.76 34
accuracy 0.90 285
macro avg 0.91 0.91 0.91 285
weighted avg 0.91 0.90 0.90 285
Confusion matrix
[[22 0 0 0 0 0 0 0 0 0]
[ 0 22 0 0 0 0 0 0 0 0]
[ 0 0 27 0 0 0 0 0 2 0]
[ 0 0 0 26 0 0 0 0 0 0]
[ 0 1 0 0 22 0 0 0 0 0]
[ 0 0 0 0 0 23 0 0 0 10]
[ 0 1 0 0 0 0 34 0 0 0]
[ 0 0 0 0 0 0 0 30 3 0]
[ 0 4 0 0 0 0 0 0 24 0]
[ 0 0 0 0 2 1 0 2 2 27]]
Iteration 2 ______________________________________________________________________
Label Spreading model: 50 labeled & 280 unlabeled (330 total)
precision recall f1-score support
0 1.00 1.00 1.00 22
1 0.85 1.00 0.92 22
2 1.00 1.00 1.00 28
3 1.00 1.00 1.00 26
4 0.87 1.00 0.93 20
5 0.96 0.70 0.81 33
6 1.00 0.97 0.99 35
7 0.94 1.00 0.97 32
8 0.92 0.86 0.89 28
9 0.73 0.79 0.76 34
accuracy 0.92 280
macro avg 0.93 0.93 0.93 280
weighted avg 0.93 0.92 0.92 280
Confusion matrix
[[22 0 0 0 0 0 0 0 0 0]
[ 0 22 0 0 0 0 0 0 0 0]
[ 0 0 28 0 0 0 0 0 0 0]
[ 0 0 0 26 0 0 0 0 0 0]
[ 0 0 0 0 20 0 0 0 0 0]
[ 0 0 0 0 0 23 0 0 0 10]
[ 0 1 0 0 0 0 34 0 0 0]
[ 0 0 0 0 0 0 0 32 0 0]
[ 0 3 0 0 1 0 0 0 24 0]
[ 0 0 0 0 2 1 0 2 2 27]]
Iteration 3 ______________________________________________________________________
Label Spreading model: 55 labeled & 275 unlabeled (330 total)
precision recall f1-score support
0 1.00 1.00 1.00 22
1 0.85 1.00 0.92 22
2 1.00 1.00 1.00 27
3 1.00 1.00 1.00 26
4 0.87 1.00 0.93 20
5 0.96 0.87 0.92 31
6 1.00 0.97 0.99 35
7 1.00 1.00 1.00 31
8 0.92 0.86 0.89 28
9 0.88 0.85 0.86 33
accuracy 0.95 275
macro avg 0.95 0.95 0.95 275
weighted avg 0.95 0.95 0.95 275
Confusion matrix
[[22 0 0 0 0 0 0 0 0 0]
[ 0 22 0 0 0 0 0 0 0 0]
[ 0 0 27 0 0 0 0 0 0 0]
[ 0 0 0 26 0 0 0 0 0 0]
[ 0 0 0 0 20 0 0 0 0 0]
[ 0 0 0 0 0 27 0 0 0 4]
[ 0 1 0 0 0 0 34 0 0 0]
[ 0 0 0 0 0 0 0 31 0 0]
[ 0 3 0 0 1 0 0 0 24 0]
[ 0 0 0 0 2 1 0 0 2 28]]
Iteration 4 ______________________________________________________________________
Label Spreading model: 60 labeled & 270 unlabeled (330 total)
precision recall f1-score support
0 1.00 1.00 1.00 22
1 0.96 1.00 0.98 22
2 1.00 0.96 0.98 27
3 0.96 1.00 0.98 25
4 0.86 1.00 0.93 19
5 0.96 0.87 0.92 31
6 1.00 0.97 0.99 35
7 1.00 1.00 1.00 31
8 0.92 0.96 0.94 25
9 0.88 0.85 0.86 33
accuracy 0.96 270
macro avg 0.95 0.96 0.96 270
weighted avg 0.96 0.96 0.96 270
Confusion matrix
[[22 0 0 0 0 0 0 0 0 0]
[ 0 22 0 0 0 0 0 0 0 0]
[ 0 0 26 1 0 0 0 0 0 0]
[ 0 0 0 25 0 0 0 0 0 0]
[ 0 0 0 0 19 0 0 0 0 0]
[ 0 0 0 0 0 27 0 0 0 4]
[ 0 1 0 0 0 0 34 0 0 0]
[ 0 0 0 0 0 0 0 31 0 0]
[ 0 0 0 0 1 0 0 0 24 0]
[ 0 0 0 0 2 1 0 0 2 28]]
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
from sklearn import datasets
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.semi_supervised import LabelSpreading
digits = datasets.load_digits()
rng = np.random.RandomState(0)
indices = np.arange(len(digits.data))
rng.shuffle(indices)
X = digits.data[indices[:330]]
y = digits.target[indices[:330]]
images = digits.images[indices[:330]]
n_total_samples = len(y)
n_labeled_points = 40
max_iterations = 5
unlabeled_indices = np.arange(n_total_samples)[n_labeled_points:]
f = plt.figure()
for i in range(max_iterations):
if len(unlabeled_indices) == 0:
print("No unlabeled items left to label.")
break
y_train = np.copy(y)
y_train[unlabeled_indices] = -1
lp_model = LabelSpreading(gamma=0.25, max_iter=20)
lp_model.fit(X, y_train)
predicted_labels = lp_model.transduction_[unlabeled_indices]
true_labels = y[unlabeled_indices]
cm = confusion_matrix(true_labels, predicted_labels, labels=lp_model.classes_)
print("Iteration %i %s" % (i, 70 * "_"))
print(
"Label Spreading model: %d labeled & %d unlabeled (%d total)"
% (n_labeled_points, n_total_samples - n_labeled_points, n_total_samples)
)
print(classification_report(true_labels, predicted_labels))
print("Confusion matrix")
print(cm)
# compute the entropies of transduced label distributions
pred_entropies = stats.distributions.entropy(lp_model.label_distributions_.T)
# select up to 5 digit examples that the classifier is most uncertain about
uncertainty_index = np.argsort(pred_entropies)[::-1]
uncertainty_index = uncertainty_index[
np.isin(uncertainty_index, unlabeled_indices)
][:5]
# keep track of indices that we get labels for
delete_indices = np.array([], dtype=int)
# for more than 5 iterations, visualize the gain only on the first 5
if i < 5:
f.text(
0.05,
(1 - (i + 1) * 0.183),
"model %d\n\nfit with\n%d labels" % ((i + 1), i * 5 + 10),
size=10,
)
for index, image_index in enumerate(uncertainty_index):
image = images[image_index]
# for more than 5 iterations, visualize the gain only on the first 5
if i < 5:
sub = f.add_subplot(5, 5, index + 1 + (5 * i))
sub.imshow(image, cmap=plt.cm.gray_r, interpolation="none")
sub.set_title(
"predict: %i\ntrue: %i"
% (lp_model.transduction_[image_index], y[image_index]),
size=10,
)
sub.axis("off")
# labeling 5 points, remote from labeled set
(delete_index,) = (unlabeled_indices == image_index).nonzero()
delete_indices = np.concatenate((delete_indices, delete_index))
unlabeled_indices = np.delete(unlabeled_indices, delete_indices)
n_labeled_points += len(uncertainty_index)
f.suptitle(
(
"Active learning with Label Propagation.\nRows show 5 most "
"uncertain labels to learn with the next model."
),
y=1.15,
)
plt.subplots_adjust(left=0.2, bottom=0.03, right=0.9, top=0.9, wspace=0.2, hspace=0.85)
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,407 Sekunden)
Verwandte Beispiele
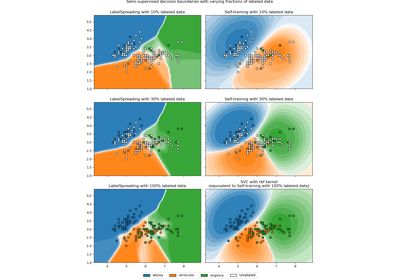
Entscheidungsgrenze semi-überwachter Klassifikatoren vs. SVM auf dem Iris-Datensatz