Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Skalierbares Lernen mit polynomieller Kernel-Approximation#
Dieses Beispiel veranschaulicht die Verwendung von PolynomialCountSketch zur effizienten Erzeugung von Kernel-Feature-Space-Approximationen für Polynomkerne. Dies wird zum Trainieren von linearen Klassifikatoren verwendet, die die Genauigkeit von kernelisierten Klassifikatoren annähern.
Wir verwenden den Covtype-Datensatz [2] und versuchen, die Experimente des Originalpapiers über Tensor Sketch [1] zu reproduzieren, d.h. den Algorithmus, der von PolynomialCountSketch implementiert wird.
Zuerst berechnen wir die Genauigkeit eines linearen Klassifikators auf den ursprünglichen Merkmalen. Dann trainieren wir lineare Klassifikatoren auf einer unterschiedlichen Anzahl von Merkmalen (n_components), die von PolynomialCountSketch generiert wurden, um die Genauigkeit eines kernelisierten Klassifikators auf skalierbare Weise zu approximieren.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Vorbereitung der Daten#
Laden des Covtype-Datensatzes, der 581.012 Stichproben mit jeweils 54 Merkmalen umfasst, verteilt auf 6 Klassen. Das Ziel dieses Datensatzes ist die Vorhersage des Wald bedeckungstyps anhand von kartografischen Variablen allein (keine Fernerkundungsdaten). Nach dem Laden wandeln wir ihn in ein binäres Klassifikationsproblem um, um ihn an die Version des Datensatzes auf der LIBSVM-Webseite [2] anzupassen, die in [1] verwendet wurde.
from sklearn.datasets import fetch_covtype
X, y = fetch_covtype(return_X_y=True)
y[y != 2] = 0
y[y == 2] = 1 # We will try to separate class 2 from the other 6 classes.
Aufteilung der Daten#
Hier wählen wir 5.000 Stichproben zum Trainieren und 10.000 zum Testen aus. Um die Ergebnisse des ursprünglichen Tensor-Sketch-Papiers tatsächlich zu reproduzieren, wählen Sie 100.000 zum Trainieren aus.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, train_size=5_000, test_size=10_000, random_state=42
)
Merkmal-Normalisierung#
Nun skalieren wir die Merkmale auf den Bereich [0, 1], um sie an das Format des Datensatzes auf der LIBSVM-Webseite anzupassen, und normalisieren sie dann auf Einheitslänge, wie im ursprünglichen Tensor-Sketch-Papier [1] geschehen.
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler, Normalizer
mm = make_pipeline(MinMaxScaler(), Normalizer())
X_train = mm.fit_transform(X_train)
X_test = mm.transform(X_test)
Festlegen eines Basismodells#
Als Basis trainieren wir einen linearen SVM auf den ursprünglichen Merkmalen und geben die Genauigkeit aus. Wir messen und speichern auch die Genauigkeiten und Trainingszeiten, um sie später zu plotten.
import time
from sklearn.svm import LinearSVC
results = {}
lsvm = LinearSVC()
start = time.time()
lsvm.fit(X_train, y_train)
lsvm_time = time.time() - start
lsvm_score = 100 * lsvm.score(X_test, y_test)
results["LSVM"] = {"time": lsvm_time, "score": lsvm_score}
print(f"Linear SVM score on raw features: {lsvm_score:.2f}%")
Linear SVM score on raw features: 75.62%
Festlegen des Kernel-Approximationsmodells#
Dann trainieren wir lineare SVMs auf den von PolynomialCountSketch generierten Merkmalen mit verschiedenen Werten für n_components, was zeigt, dass diese Kernel-Feature-Approximationen die Genauigkeit der linearen Klassifizierung verbessern. In typischen Anwendungsszenarien sollte n_components größer sein als die Anzahl der Merkmale in der Eingaberepräsentation, um eine Verbesserung gegenüber der linearen Klassifizierung zu erzielen. Als Faustregel wird das Optimum der Evaluationsmetrik / Laufzeitkosten typischerweise bei etwa n_components = 10 * n_features erreicht, obwohl dies vom spezifischen behandelten Datensatz abhängen kann. Beachten Sie, dass da die ursprünglichen Stichproben 54 Merkmale haben, die explizite Feature-Map des Polynomkernels vom vierten Grad etwa 8,5 Millionen Merkmale hätte (genau: 54^4). Dank PolynomialCountSketch können wir die meiste diskriminierende Information dieses Feature-Raums in einer viel kompakteren Repräsentation kondensieren. Obwohl wir das Experiment in diesem Beispiel nur einmal (n_runs = 1) ausführen, sollte man in der Praxis das Experiment mehrmals wiederholen, um die stochastische Natur von PolynomialCountSketch auszugleichen.
from sklearn.kernel_approximation import PolynomialCountSketch
n_runs = 1
N_COMPONENTS = [250, 500, 1000, 2000]
for n_components in N_COMPONENTS:
ps_lsvm_time = 0
ps_lsvm_score = 0
for _ in range(n_runs):
pipeline = make_pipeline(
PolynomialCountSketch(n_components=n_components, degree=4),
LinearSVC(),
)
start = time.time()
pipeline.fit(X_train, y_train)
ps_lsvm_time += time.time() - start
ps_lsvm_score += 100 * pipeline.score(X_test, y_test)
ps_lsvm_time /= n_runs
ps_lsvm_score /= n_runs
results[f"LSVM + PS({n_components})"] = {
"time": ps_lsvm_time,
"score": ps_lsvm_score,
}
print(
f"Linear SVM score on {n_components} PolynomialCountSketch "
f"features: {ps_lsvm_score:.2f}%"
)
Linear SVM score on 250 PolynomialCountSketch features: 76.55%
Linear SVM score on 500 PolynomialCountSketch features: 76.92%
Linear SVM score on 1000 PolynomialCountSketch features: 77.79%
Linear SVM score on 2000 PolynomialCountSketch features: 78.59%
Festlegen des kernelisierten SVM-Modells#
Trainieren Sie einen kernelisierten SVM, um zu sehen, wie gut PolynomialCountSketch die Leistung des Kernels approximiert. Dies kann natürlich einige Zeit dauern, da die SVC-Klasse eine relativ schlechte Skalierbarkeit aufweist. Das ist der Grund, warum Kernel-Approximatoren so nützlich sind.
from sklearn.svm import SVC
ksvm = SVC(C=500.0, kernel="poly", degree=4, coef0=0, gamma=1.0)
start = time.time()
ksvm.fit(X_train, y_train)
ksvm_time = time.time() - start
ksvm_score = 100 * ksvm.score(X_test, y_test)
results["KSVM"] = {"time": ksvm_time, "score": ksvm_score}
print(f"Kernel-SVM score on raw features: {ksvm_score:.2f}%")
Kernel-SVM score on raw features: 79.78%
Vergleich der Ergebnisse#
Zum Schluss plotten wir die Ergebnisse der verschiedenen Methoden im Verhältnis zu ihren Trainingszeiten. Wie wir sehen können, erzielt der kernelisierte SVM eine höhere Genauigkeit, aber seine Trainingszeit ist viel größer und vor allem wächst sie viel schneller, wenn die Anzahl der Trainingsstichproben steigt.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(
[
results["LSVM"]["time"],
],
[
results["LSVM"]["score"],
],
label="Linear SVM",
c="green",
marker="^",
)
ax.scatter(
[
results["LSVM + PS(250)"]["time"],
],
[
results["LSVM + PS(250)"]["score"],
],
label="Linear SVM + PolynomialCountSketch",
c="blue",
)
for n_components in N_COMPONENTS:
ax.scatter(
[
results[f"LSVM + PS({n_components})"]["time"],
],
[
results[f"LSVM + PS({n_components})"]["score"],
],
c="blue",
)
ax.annotate(
f"n_comp.={n_components}",
(
results[f"LSVM + PS({n_components})"]["time"],
results[f"LSVM + PS({n_components})"]["score"],
),
xytext=(-30, 10),
textcoords="offset pixels",
)
ax.scatter(
[
results["KSVM"]["time"],
],
[
results["KSVM"]["score"],
],
label="Kernel SVM",
c="red",
marker="x",
)
ax.set_xlabel("Training time (s)")
ax.set_ylabel("Accuracy (%)")
ax.legend()
plt.show()

Referenzen#
Gesamtlaufzeit des Skripts: (0 Minuten 39,458 Sekunden)
Verwandte Beispiele
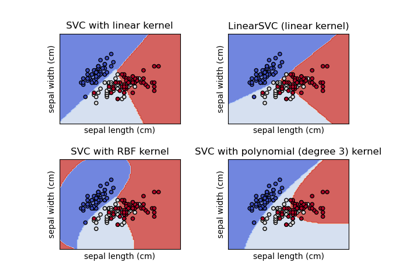
Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten