Clustering von Textdokumenten mit k-Means

Dies ist ein Beispiel, das zeigt, wie die scikit-learn API verwendet werden kann, um Dokumente nach Themen mithilfe eines Bag of Words-Ansatzes zu clustern.

Zwei Algorithmen werden demonstriert, nämlich KMeans und seine skalierbarere Variante, MiniBatchKMeans. Zusätzlich wird latente semantische Analyse verwendet, um die Dimensionalität zu reduzieren und latente Muster in den Daten zu entdecken.

Dieses Beispiel verwendet zwei verschiedene Text-Vektorisierer: einen TfidfVectorizer und einen HashingVectorizer. Weitere Informationen zu Vektorisierern und einen Vergleich ihrer Verarbeitungszeiten finden Sie im Beispiel-Notebook Vergleich von HashingVectorizer und DictVectorizer.

Für die Dokumentenanalyse mittels eines überwachten Lernansatzes siehe das Beispielskript Klassifizierung von Textdokumenten mit spärlichen Merkmalen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Laden von Textdaten

Wir laden Daten aus dem 20 Newsgroups Textdatensatz, der rund 18.000 Newsgroups-Beiträge zu 20 Themen umfasst. Zu Illustrationszwecken und zur Reduzierung des Rechenaufwands wählen wir nur einen Teilsatz von 4 Themen aus, der etwa 3.400 Dokumente umfasst. Sehen Sie das Beispiel Klassifizierung von Textdokumenten mit spärlichen Merkmalen, um eine Intuition über die Überschneidung solcher Themen zu gewinnen.

Beachten Sie, dass die Textbeispiele standardmäßig einige Nachrichtenmetadaten wie "headers", "footers" (Signaturen) und "quotes" zu anderen Beiträgen enthalten. Wir verwenden den Parameter remove von fetch_20newsgroups, um diese Merkmale zu entfernen und ein sinnvolleres Clustering-Problem zu haben.

import numpy as np

from sklearn.datasets import fetch_20newsgroups

categories = [
    "alt.atheism",
    "talk.religion.misc",
    "comp.graphics",
    "sci.space",
]

dataset = fetch_20newsgroups(
    remove=("headers", "footers", "quotes"),
    subset="all",
    categories=categories,
    shuffle=True,
    random_state=42,
)

labels = dataset.target
unique_labels, category_sizes = np.unique(labels, return_counts=True)
true_k = unique_labels.shape[0]

print(f"{len(dataset.data)} documents - {true_k} categories")

3387 documents - 4 categories

Quantifizierung der Qualität von Clustering-Ergebnissen

In diesem Abschnitt definieren wir eine Funktion, um verschiedene Clustering-Pipelines anhand mehrerer Metriken zu bewerten.

Clustering-Algorithmen sind grundsätzlich unüberwachte Lernmethoden. Da wir jedoch für diesen spezifischen Datensatz Klassenbezeichnungen haben, ist es möglich, Bewertungsmetriken zu verwenden, die diese "überwachten" Ground-Truth-Informationen nutzen, um die Qualität der resultierenden Cluster zu quantifizieren. Beispiele für solche Metriken sind die folgenden:

• Homogenität (Homogeneity), die quantifiziert, wie sehr Cluster nur Mitglieder einer einzigen Klasse enthalten;

• Vollständigkeit (Completeness), die quantifiziert, wie sehr Mitglieder einer gegebenen Klasse denselben Clustern zugeordnet werden;

• V-Maß (V-measure), das harmonische Mittel aus Vollständigkeit und Homogenität;

• Rand-Index (Rand Index), der misst, wie häufig Paare von Datenpunkten konsistent gemäß dem Ergebnis des Clustering-Algorithmus und der Ground-Truth-Klassenbezeichnung gruppiert werden;

• Angepasster Rand-Index (Adjusted Rand Index), ein zufallsbereinigter Rand-Index, sodass zufällige Clusterzuweisungen im Erwartungswert einen ARI von 0,0 haben.

Wenn die Ground-Truth-Labels nicht bekannt sind, kann die Bewertung nur anhand der Modellergebnisse selbst erfolgen. In diesem Fall ist der Silhouettenkoeffizient (Silhouette Coefficient) hilfreich. Sehen Sie das Beispiel Auswahl der Anzahl von Clustern mit Silhouettenanalyse bei k-Means-Clustering für ein Beispiel, wie dies gemacht wird.

Für weitere Referenzen siehe Bewertung der Clustering-Leistung.

from collections import defaultdict
from time import time

from sklearn import metrics

evaluations = []
evaluations_std = []


def fit_and_evaluate(km, X, name=None, n_runs=5):
    name = km.__class__.__name__ if name is None else name

    train_times = []
    scores = defaultdict(list)
    for seed in range(n_runs):
        km.set_params(random_state=seed)
        t0 = time()
        km.fit(X)
        train_times.append(time() - t0)
        scores["Homogeneity"].append(metrics.homogeneity_score(labels, km.labels_))
        scores["Completeness"].append(metrics.completeness_score(labels, km.labels_))
        scores["V-measure"].append(metrics.v_measure_score(labels, km.labels_))
        scores["Adjusted Rand-Index"].append(
            metrics.adjusted_rand_score(labels, km.labels_)
        )
        scores["Silhouette Coefficient"].append(
            metrics.silhouette_score(X, km.labels_, sample_size=2000)
        )
    train_times = np.asarray(train_times)

    print(f"clustering done in {train_times.mean():.2f} ± {train_times.std():.2f} s ")
    evaluation = {
        "estimator": name,
        "train_time": train_times.mean(),
    }
    evaluation_std = {
        "estimator": name,
        "train_time": train_times.std(),
    }
    for score_name, score_values in scores.items():
        mean_score, std_score = np.mean(score_values), np.std(score_values)
        print(f"{score_name}: {mean_score:.3f} ± {std_score:.3f}")
        evaluation[score_name] = mean_score
        evaluation_std[score_name] = std_score
    evaluations.append(evaluation)
    evaluations_std.append(evaluation_std)

k-Means-Clustering auf Textmerkmalen

In diesem Beispiel werden zwei Merkmalsextraktionsmethoden verwendet:

• TfidfVectorizer verwendet ein In-Memory-Vokabular (ein Python-Dict), um die häufigsten Wörter zu Merkmalsindizes abzubilden und somit eine Worthäufigkeitsmatrix (spärlich) zu berechnen. Die Worthäufigkeiten werden dann mithilfe des inversen Dokumentenwerts (IDF) neu gewichtet, der spaltenweise über den Korpus gesammelt wird.

• HashingVectorizer hasht Worthäufigkeiten in einen festen dimensionalen Raum, möglicherweise mit Kollisionen. Die Worthäufigkeitsvektoren werden dann so normalisiert, dass jeder eine l2-Norm von eins hat (projiziert auf die Euklidische Einheitssphäre), was für das Funktionieren von k-Means im hochdimensionalen Raum wichtig zu sein scheint.

Darüber hinaus ist es möglich, diese extrahierten Merkmale mittels Dimensionsreduktion nachzubearbeiten. Wir werden die Auswirkungen dieser Entscheidungen auf die Clustering-Qualität im Folgenden untersuchen.

Merkmalsextraktion mit TfidfVectorizer

Wir benchmarken zunächst die Schätzer mit einem Dictionary-Vektorisierer zusammen mit einer IDF-Normalisierung, wie sie von TfidfVectorizer bereitgestellt wird.

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer(
    max_df=0.5,
    min_df=5,
    stop_words="english",
)
t0 = time()
X_tfidf = vectorizer.fit_transform(dataset.data)

print(f"vectorization done in {time() - t0:.3f} s")
print(f"n_samples: {X_tfidf.shape[0]}, n_features: {X_tfidf.shape[1]}")

vectorization done in 0.333 s
n_samples: 3387, n_features: 7929

Nachdem Begriffe, die in mehr als 50 % der Dokumente vorkommen (gesetzt durch max_df=0.5), und Begriffe, die in mindestens 5 Dokumenten nicht vorhanden sind (gesetzt durch min_df=5), ignoriert werden, beträgt die resultierende Anzahl eindeutiger Begriffe n_features etwa 8.000. Wir können zusätzlich die Spärlichkeit der X_tfidf-Matrix als Anteil der Nicht-Null-Einträge geteilt durch die Gesamtzahl der Elemente quantifizieren.

print(f"{X_tfidf.nnz / np.prod(X_tfidf.shape):.3f}")

0.007

Wir stellen fest, dass etwa 0,7 % der Einträge der X_tfidf-Matrix nicht-null sind.

Clustering spärlicher Daten mit k-Means

Da sowohl KMeans als auch MiniBatchKMeans eine nicht-konvexe Zielfunktion optimieren, ist ihr Clustering nicht garantiert optimal für eine gegebene zufällige Initialisierung. Darüber hinaus können k-Means auf spärlichen, hochdimensionalen Daten wie textbasierten Bag-of-Words-Ansätzen Zentroiden auf extrem isolierten Datenpunkten initialisieren. Diese Datenpunkte können ihre eigenen Zentroiden bleiben.

Der folgende Code veranschaulicht, wie das zuvor genannte Phänomen manchmal zu stark unausgewogenen Clustern führen kann, abhängig von der zufälligen Initialisierung.

from sklearn.cluster import KMeans

for seed in range(5):
    kmeans = KMeans(
        n_clusters=true_k,
        max_iter=100,
        n_init=1,
        random_state=seed,
    ).fit(X_tfidf)
    cluster_ids, cluster_sizes = np.unique(kmeans.labels_, return_counts=True)
    print(f"Number of elements assigned to each cluster: {cluster_sizes}")
print()
print(
    "True number of documents in each category according to the class labels: "
    f"{category_sizes}"
)

Number of elements assigned to each cluster: [ 481  675 1785  446]
Number of elements assigned to each cluster: [1689  638  480  580]
Number of elements assigned to each cluster: [   1    1    1 3384]
Number of elements assigned to each cluster: [1887  311  332  857]
Number of elements assigned to each cluster: [ 291  673 1771  652]

True number of documents in each category according to the class labels: [799 973 987 628]

Um dieses Problem zu vermeiden, ist eine Möglichkeit, die Anzahl der Durchläufe mit unabhängigen zufälligen Initialisierungen n_init zu erhöhen. In diesem Fall wird das Clustering mit der besten Trägheit (Zielfunktion von k-Means) gewählt.

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=5,
)

fit_and_evaluate(kmeans, X_tfidf, name="KMeans\non tf-idf vectors")

clustering done in 0.17 ± 0.04 s
Homogeneity: 0.349 ± 0.010
Completeness: 0.398 ± 0.009
V-measure: 0.372 ± 0.009
Adjusted Rand-Index: 0.203 ± 0.017
Silhouette Coefficient: 0.007 ± 0.000

Alle diese Clustering-Bewertungsmetriken haben einen Maximalwert von 1,0 (für ein perfektes Clustering-Ergebnis). Höhere Werte sind besser. Werte des angepassten Rand-Indexes nahe 0,0 entsprechen einer zufälligen Beschriftung. Beachten Sie aus den obigen Bewertungen, dass die Clusterzuweisung tatsächlich gut über dem Zufallsniveau liegt, aber die Gesamtqualität sicherlich verbessert werden kann.

Beachten Sie, dass die Klassenbezeichnungen die Dokumententhemen möglicherweise nicht genau widerspiegeln und daher Metriken, die Labels verwenden, nicht unbedingt die besten zur Bewertung der Qualität unserer Clustering-Pipeline sind.

Durchführung der Dimensionsreduktion mit LSA

Ein n_init=1 kann immer noch verwendet werden, solange die Dimension des vektorisierten Raums zuerst reduziert wird, um k-Means stabiler zu machen. Zu diesem Zweck verwenden wir TruncatedSVD, das auf Begriffszählungs-/TF-IDF-Matrizen arbeitet. Da SVD-Ergebnisse nicht normalisiert sind, führen wir die Normalisierung erneut durch, um das KMeans-Ergebnis zu verbessern. Die Verwendung von SVD zur Reduzierung der Dimensionalität von TF-IDF-Dokumentvektoren ist in der Information-Retrieval- und Text-Mining-Literatur oft als latente semantische Analyse (LSA) bekannt.

from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer

lsa = make_pipeline(TruncatedSVD(n_components=100), Normalizer(copy=False))
t0 = time()
X_lsa = lsa.fit_transform(X_tfidf)
explained_variance = lsa[0].explained_variance_ratio_.sum()

print(f"LSA done in {time() - t0:.3f} s")
print(f"Explained variance of the SVD step: {explained_variance * 100:.1f}%")

LSA done in 0.336 s
Explained variance of the SVD step: 18.4%

Die Verwendung einer einzigen Initialisierung bedeutet, dass die Verarbeitungszeit sowohl für KMeans als auch für MiniBatchKMeans reduziert wird.

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=1,
)

fit_and_evaluate(kmeans, X_lsa, name="KMeans\nwith LSA on tf-idf vectors")

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.398 ± 0.011
Completeness: 0.427 ± 0.025
V-measure: 0.412 ± 0.017
Adjusted Rand-Index: 0.321 ± 0.018
Silhouette Coefficient: 0.029 ± 0.001

Wir können beobachten, dass das Clustering auf der LSA-Repräsentation des Dokuments deutlich schneller ist (sowohl wegen n_init=1 als auch weil die Dimensionalität des LSA-Merkmalsraums viel geringer ist). Darüber hinaus haben sich alle Clustering-Bewertungsmetriken verbessert. Wir wiederholen das Experiment mit MiniBatchKMeans.

from sklearn.cluster import MiniBatchKMeans

minibatch_kmeans = MiniBatchKMeans(
    n_clusters=true_k,
    n_init=1,
    init_size=1000,
    batch_size=1000,
)

fit_and_evaluate(
    minibatch_kmeans,
    X_lsa,
    name="MiniBatchKMeans\nwith LSA on tf-idf vectors",
)

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.333 ± 0.084
Completeness: 0.351 ± 0.066
V-measure: 0.341 ± 0.076
Adjusted Rand-Index: 0.290 ± 0.060
Silhouette Coefficient: 0.026 ± 0.004

Top-Begriffe pro Cluster

Da TfidfVectorizer invertierbar ist, können wir die Clusterzentren identifizieren, die eine Intuition für die einflussreichsten Wörter **für jeden Cluster** liefern. Sehen Sie das Beispielskript Klassifizierung von Textdokumenten mit spärlichen Merkmalen für einen Vergleich mit den prädiktivsten Wörtern **für jede Zielklasse**.

original_space_centroids = lsa[0].inverse_transform(kmeans.cluster_centers_)
order_centroids = original_space_centroids.argsort()[:, ::-1]
terms = vectorizer.get_feature_names_out()

for i in range(true_k):
    print(f"Cluster {i}: ", end="")
    for ind in order_centroids[i, :10]:
        print(f"{terms[ind]} ", end="")
    print()

Cluster 0: thanks graphics image know files file program looking software does
Cluster 1: space launch orbit nasa shuttle earth moon like mission just
Cluster 2: god jesus bible believe christian faith people say does christians
Cluster 3: think don people just say know like time did does

HashingVectorizer

Eine alternative Vektorisierung kann mit einer Instanz von HashingVectorizer erfolgen, die keine IDF-Gewichtung bietet, da dies ein zustandsloses Modell ist (die `fit`-Methode tut nichts). Wenn IDF-Gewichtung benötigt wird, kann sie durch Verketten der Ausgabe von HashingVectorizer mit einer Instanz von TfidfTransformer hinzugefügt werden. In diesem Fall fügen wir LSA auch der Pipeline hinzu, um die Dimensionalität und Spärlichkeit des gehashten Vektorraums zu reduzieren.

from sklearn.feature_extraction.text import HashingVectorizer, TfidfTransformer

lsa_vectorizer = make_pipeline(
    HashingVectorizer(stop_words="english", n_features=50_000),
    TfidfTransformer(),
    TruncatedSVD(n_components=100, random_state=0),
    Normalizer(copy=False),
)

t0 = time()
X_hashed_lsa = lsa_vectorizer.fit_transform(dataset.data)
print(f"vectorization done in {time() - t0:.3f} s")

vectorization done in 1.647 s

Man kann beobachten, dass der LSA-Schritt relativ lange zum Anpassen dauert, insbesondere mit gehashten Vektoren. Der Grund dafür ist, dass ein gehashter Raum typischerweise groß ist (in diesem Beispiel auf n_features=50_000 gesetzt). Man kann versuchen, die Anzahl der Merkmale zu verringern, auf Kosten eines größeren Anteils an Merkmalen mit Hash-Kollisionen, wie im Beispiel-Notebook Vergleich von HashingVectorizer und DictVectorizer gezeigt.

Wir passen und bewerten nun die Instanzen kmeans und minibatch_kmeans auf diesen gehasht-LSA-reduzierten Daten.

fit_and_evaluate(kmeans, X_hashed_lsa, name="KMeans\nwith LSA on hashed vectors")

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.390 ± 0.008
Completeness: 0.436 ± 0.012
V-measure: 0.411 ± 0.010
Adjusted Rand-Index: 0.322 ± 0.014
Silhouette Coefficient: 0.030 ± 0.001

fit_and_evaluate(
    minibatch_kmeans,
    X_hashed_lsa,
    name="MiniBatchKMeans\nwith LSA on hashed vectors",
)

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.359 ± 0.053
Completeness: 0.385 ± 0.059
V-measure: 0.371 ± 0.055
Adjusted Rand-Index: 0.315 ± 0.046
Silhouette Coefficient: 0.029 ± 0.002

Beide Methoden führen zu guten Ergebnissen, die denen der Ausführung derselben Modelle auf den traditionellen LSA-Vektoren (ohne Hashing) ähneln.

Zusammenfassung der Clustering-Bewertung

import matplotlib.pyplot as plt
import pandas as pd

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(16, 6), sharey=True)

df = pd.DataFrame(evaluations[::-1]).set_index("estimator")
df_std = pd.DataFrame(evaluations_std[::-1]).set_index("estimator")

df.drop(
    ["train_time"],
    axis="columns",
).plot.barh(ax=ax0, xerr=df_std)
ax0.set_xlabel("Clustering scores")
ax0.set_ylabel("")

df["train_time"].plot.barh(ax=ax1, xerr=df_std["train_time"])
ax1.set_xlabel("Clustering time (s)")
plt.tight_layout()

KMeans und MiniBatchKMeans leiden unter dem Phänomen namens Fluch der Dimensionalität für hochdimensionale Datensätze wie Textdaten. Aus diesem Grund verbessern sich die Gesamtbewertungen bei Verwendung von LSA. Die Verwendung von LSA-reduzierten Daten verbessert auch die Stabilität und erfordert eine geringere Clustering-Zeit, obwohl zu beachten ist, dass der LSA-Schritt selbst lange dauert, insbesondere mit gehashten Vektoren.

Der Silhouettenkoeffizient ist zwischen 0 und 1 definiert. In allen Fällen erhalten wir Werte nahe 0 (auch wenn sie sich nach Verwendung von LSA etwas verbessern), da seine Definition Abstände messen muss, im Gegensatz zu anderen Bewertungsmetriken wie dem V-Maß und dem Angepassten Rand-Index, die nur auf Clusterzuweisungen und nicht auf Abstände basieren. Beachten Sie, dass man streng genommen den Silhouettenkoeffizienten zwischen Räumen unterschiedlicher Dimension nicht vergleichen sollte, aufgrund der unterschiedlichen Distanzbegriffe, die sie implizieren.

Die Homogenitäts-, Vollständigkeits- und somit V-Maß-Metriken liefern keine Baseline in Bezug auf zufällige Beschriftungen: Dies bedeutet, dass je nach Anzahl der Stichproben, Cluster und Ground-Truth-Klassen eine vollständig zufällige Beschriftung nicht immer dieselben Werte liefert. Insbesondere zufällige Beschriftungen ergeben nicht immer Null-Werte, insbesondere wenn die Anzahl der Cluster groß ist. Dieses Problem kann bei mehr als tausend Stichproben und weniger als 10 Clustern, wie im vorliegenden Beispiel, sicher ignoriert werden. Für kleinere Stichprobengrößen oder eine größere Anzahl von Clustern ist es sicherer, einen angepassten Index wie den Angepassten Rand-Index (ARI) zu verwenden. Sehen Sie das Beispiel Anpassung für Zufall bei der Bewertung der Clustering-Leistung für eine Demonstration der Auswirkung zufälliger Beschriftungen.

Die Größe der Fehlerbalken zeigt, dass MiniBatchKMeans für diesen relativ kleinen Datensatz weniger stabil ist als KMeans. Es ist interessanter, wenn die Anzahl der Stichproben viel größer ist, kann dies jedoch auf Kosten einer geringen Verschlechterung der Clustering-Qualität im Vergleich zum traditionellen k-Means-Algorithmus gehen.

Verwandte Beispiele

Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten

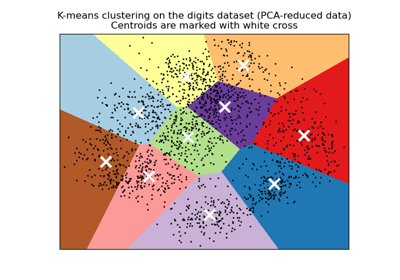
Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten

Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

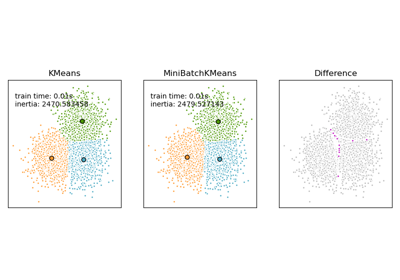
Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

Biclustering von Dokumenten mit dem Spectral Co-Clustering Algorithmus

Biclustering von Dokumenten mit dem Spectral Co-Clustering Algorithmus

Klassifikation von Textdokumenten mit spärlichen Merkmalen

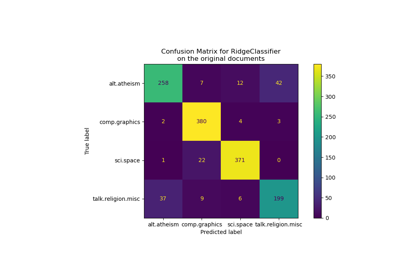
Klassifikation von Textdokumenten mit spärlichen Merkmalen