Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel in Ihrem Browser über JupyterLite oder Binder auszuführen.
Robuste vs. empirische Kovarianzschätzung#
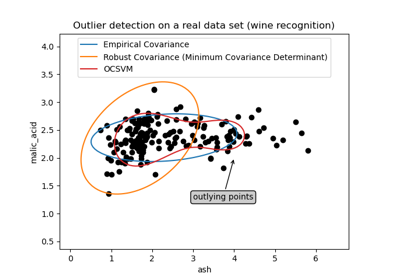
Die übliche Maximum-Likelihood-Schätzung der Kovarianz ist sehr empfindlich gegenüber dem Vorhandensein von Ausreißern im Datensatz. In einem solchen Fall wäre es besser, einen robusten Schätzer für die Kovarianz zu verwenden, um sicherzustellen, dass die Schätzung unempfindlich gegenüber „fehlerhaften“ Beobachtungen im Datensatz ist. [1], [2]
Minimum Covariance Determinant Estimator#
Der Minimum Covariance Determinant (MCD) Schätzer ist ein robuster Schätzer für die Kovarianz mit einem hohen Break-Down-Punkt (d. h. er kann zur Schätzung der Kovarianzmatrix stark kontaminierter Datensätze verwendet werden, bis zu \(\frac{n_\text{samples} - n_\text{features}-1}{2}\) Ausreißer). Die Idee ist, \(\frac{n_\text{samples} + n_\text{features}+1}{2}\) Beobachtungen zu finden, deren empirische Kovarianz die kleinste Determinante hat, was zu einer „reinen“ Teilmenge von Beobachtungen führt, aus denen Standardschätzungen für Ort und Kovarianz berechnet werden. Nach einem Korrekturschritt, der darauf abzielt, die Tatsache zu kompensieren, dass die Schätzungen nur aus einem Teil der ursprünglichen Daten gelernt wurden, erhalten wir robuste Schätzungen für Ort und Kovarianz des Datensatzes.
Der Minimum Covariance Determinant Estimator (MCD) wurde von P.J.Rousseuw in [3] eingeführt.
Auswertung#
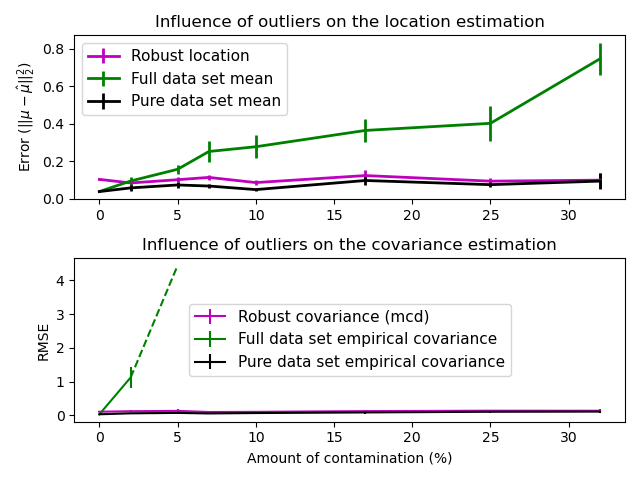
In diesem Beispiel vergleichen wir die Schätzfehler, die bei der Verwendung verschiedener Arten von Ort- und Kovarianzschätzungen auf kontaminierten Gauß-verteilten Datensätzen auftreten
Der Mittelwert und die empirische Kovarianz des gesamten Datensatzes, die zusammenbrechen, sobald Ausreißer im Datensatz vorhanden sind
Der robuste MCD, der einen geringen Fehler aufweist, vorausgesetzt \(n_\text{samples} > 5n_\text{features}\)
Der Mittelwert und die empirische Kovarianz der Beobachtungen, die als gut bekannt sind. Dies kann als eine „perfekte“ MCD-Schätzung betrachtet werden, sodass man unserer Implementierung vertrauen kann, indem man mit diesem Fall vergleicht.
Referenzen#
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.font_manager
import matplotlib.pyplot as plt
import numpy as np
from sklearn.covariance import EmpiricalCovariance, MinCovDet
# example settings
n_samples = 80
n_features = 5
repeat = 10
range_n_outliers = np.concatenate(
(
np.linspace(0, n_samples / 8, 5),
np.linspace(n_samples / 8, n_samples / 2, 5)[1:-1],
)
).astype(int)
# definition of arrays to store results
err_loc_mcd = np.zeros((range_n_outliers.size, repeat))
err_cov_mcd = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_full = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_full = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_pure = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_pure = np.zeros((range_n_outliers.size, repeat))
# computation
for i, n_outliers in enumerate(range_n_outliers):
for j in range(repeat):
rng = np.random.RandomState(i * j)
# generate data
X = rng.randn(n_samples, n_features)
# add some outliers
outliers_index = rng.permutation(n_samples)[:n_outliers]
outliers_offset = 10.0 * (
np.random.randint(2, size=(n_outliers, n_features)) - 0.5
)
X[outliers_index] += outliers_offset
inliers_mask = np.ones(n_samples).astype(bool)
inliers_mask[outliers_index] = False
# fit a Minimum Covariance Determinant (MCD) robust estimator to data
mcd = MinCovDet().fit(X)
# compare raw robust estimates with the true location and covariance
err_loc_mcd[i, j] = np.sum(mcd.location_**2)
err_cov_mcd[i, j] = mcd.error_norm(np.eye(n_features))
# compare estimators learned from the full data set with true
# parameters
err_loc_emp_full[i, j] = np.sum(X.mean(0) ** 2)
err_cov_emp_full[i, j] = (
EmpiricalCovariance().fit(X).error_norm(np.eye(n_features))
)
# compare with an empirical covariance learned from a pure data set
# (i.e. "perfect" mcd)
pure_X = X[inliers_mask]
pure_location = pure_X.mean(0)
pure_emp_cov = EmpiricalCovariance().fit(pure_X)
err_loc_emp_pure[i, j] = np.sum(pure_location**2)
err_cov_emp_pure[i, j] = pure_emp_cov.error_norm(np.eye(n_features))
# Display results
font_prop = matplotlib.font_manager.FontProperties(size=11)
plt.subplot(2, 1, 1)
lw = 2
plt.errorbar(
range_n_outliers,
err_loc_mcd.mean(1),
yerr=err_loc_mcd.std(1) / np.sqrt(repeat),
label="Robust location",
lw=lw,
color="m",
)
plt.errorbar(
range_n_outliers,
err_loc_emp_full.mean(1),
yerr=err_loc_emp_full.std(1) / np.sqrt(repeat),
label="Full data set mean",
lw=lw,
color="green",
)
plt.errorbar(
range_n_outliers,
err_loc_emp_pure.mean(1),
yerr=err_loc_emp_pure.std(1) / np.sqrt(repeat),
label="Pure data set mean",
lw=lw,
color="black",
)
plt.title("Influence of outliers on the location estimation")
plt.ylabel(r"Error ($||\mu - \hat{\mu}||_2^2$)")
plt.legend(loc="upper left", prop=font_prop)
plt.subplot(2, 1, 2)
x_size = range_n_outliers.size
plt.errorbar(
range_n_outliers,
err_cov_mcd.mean(1),
yerr=err_cov_mcd.std(1),
label="Robust covariance (mcd)",
color="m",
)
plt.errorbar(
range_n_outliers[: (x_size // 5 + 1)],
err_cov_emp_full.mean(1)[: (x_size // 5 + 1)],
yerr=err_cov_emp_full.std(1)[: (x_size // 5 + 1)],
label="Full data set empirical covariance",
color="green",
)
plt.plot(
range_n_outliers[(x_size // 5) : (x_size // 2 - 1)],
err_cov_emp_full.mean(1)[(x_size // 5) : (x_size // 2 - 1)],
color="green",
ls="--",
)
plt.errorbar(
range_n_outliers,
err_cov_emp_pure.mean(1),
yerr=err_cov_emp_pure.std(1),
label="Pure data set empirical covariance",
color="black",
)
plt.title("Influence of outliers on the covariance estimation")
plt.xlabel("Amount of contamination (%)")
plt.ylabel("RMSE")
plt.legend(loc="center", prop=font_prop)
plt.tight_layout()
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 2,515 Sekunden)
Verwandte Beispiele
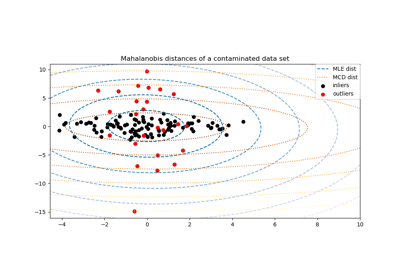
Robuste Kovarianzschätzung und Relevanz von Mahalanobis-Distanzen
Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid