Hinweis

Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

Unterstützung kategorialer Merkmale in Gradient Boosting#

In diesem Beispiel vergleichen wir die Trainingszeiten und Vorhersageleistungen von HistGradientBoostingRegressor mit verschiedenen Kodierungsstrategien für kategoriale Merkmale. Insbesondere evaluieren wir

„Dropped“: Entfernen der kategorialen Merkmale;
„One Hot“: Verwendung eines OneHotEncoder;
„Ordinal“: Verwendung eines OrdinalEncoder und Behandlung von Kategorien als geordnete, äquidistante Mengen;
„Target“: Verwendung eines TargetEncoder;
„Native“: Verlassen auf die native Unterstützung für Kategorien des HistGradientBoostingRegressor-Schätzers.

Zu diesem Zweck verwenden wir den Ames Iowa Housing Datensatz, der aus numerischen und kategorialen Merkmalen besteht, wobei das Ziel der Verkaufspreis des Hauses ist.

Siehe Merkmale in Histogramm-Gradient-Boosting-Bäumen für ein Beispiel, das einige andere Merkmale von HistGradientBoostingRegressor zeigt.

Siehe Vergleich von Target Encoder mit anderen Encodern für einen Vergleich von Kodierungsstrategien in Gegenwart von kategorialen Merkmalen mit hoher Kardinalität.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Laden des Ames Housing Datensatzes#

Zuerst laden wir die Ames Housing Daten als Pandas DataFrame. Die Merkmale sind entweder kategorial oder numerisch.

from sklearn.datasets import fetch_openml

X, y = fetch_openml(data_id=42165, as_frame=True, return_X_y=True)

# Select only a subset of features of X to make the example faster to run
categorical_columns_subset = [
    "BldgType",
    "GarageFinish",
    "LotConfig",
    "Functional",
    "MasVnrType",
    "HouseStyle",
    "FireplaceQu",
    "ExterCond",
    "ExterQual",
    "PoolQC",
]

numerical_columns_subset = [
    "3SsnPorch",
    "Fireplaces",
    "BsmtHalfBath",
    "HalfBath",
    "GarageCars",
    "TotRmsAbvGrd",
    "BsmtFinSF1",
    "BsmtFinSF2",
    "GrLivArea",
    "ScreenPorch",
]

X = X[categorical_columns_subset + numerical_columns_subset]
X[categorical_columns_subset] = X[categorical_columns_subset].astype("category")

categorical_columns = X.select_dtypes(include="category").columns
n_categorical_features = len(categorical_columns)
n_numerical_features = X.select_dtypes(include="number").shape[1]

print(f"Number of samples: {X.shape[0]}")
print(f"Number of features: {X.shape[1]}")
print(f"Number of categorical features: {n_categorical_features}")
print(f"Number of numerical features: {n_numerical_features}")

Number of samples: 1460
Number of features: 20
Number of categorical features: 10
Number of numerical features: 10

Gradient Boosting Schätzer mit entfernten kategorialen Merkmalen#

Als Basis erstellen wir einen Schätzer, bei dem die kategorialen Merkmale entfernt werden.

from sklearn.compose import make_column_selector, make_column_transformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.pipeline import make_pipeline

dropper = make_column_transformer(
    ("drop", make_column_selector(dtype_include="category")), remainder="passthrough"
)
hist_dropped = make_pipeline(dropper, HistGradientBoostingRegressor(random_state=42))
hist_dropped

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('drop', 'drop',
                                                  <sklearn.compose._column_transformer.make_column_selector object at 0x7fb4a2b293d0>)])),
                ('histgradientboostingregressor',
                 HistGradientBoostingRegressor(random_state=42))])

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Gradient Boosting Schätzer mit One-Hot-Kodierung#

Als nächstes erstellen wir eine Pipeline, um kategoriale Merkmale mittels One-Hot-Kodierung zu transformieren, während die verbleibenden Merkmale unverändert als "passthrough" behandelt werden.

from sklearn.preprocessing import OneHotEncoder

one_hot_encoder = make_column_transformer(
    (
        OneHotEncoder(sparse_output=False, handle_unknown="ignore"),
        make_column_selector(dtype_include="category"),
    ),
    remainder="passthrough",
)

hist_one_hot = make_pipeline(
    one_hot_encoder, HistGradientBoostingRegressor(random_state=42)
)
hist_one_hot

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore',
                                                                sparse_output=False),
                                                  <sklearn.compose._column_transformer.make_column_selector object at 0x7fb4a2b28f50>)])),
                ('histgradientboostingregressor',
                 HistGradientBoostingRegressor(random_state=42))])

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Gradient Boosting Schätzer mit ordinaler Kodierung#

Als nächstes erstellen wir eine Pipeline, die kategoriale Merkmale als geordnete Mengen behandelt, d.h. die Kategorien werden als 0, 1, 2 usw. kodiert und als kontinuierliche Merkmale behandelt.

import numpy as np

from sklearn.preprocessing import OrdinalEncoder

ordinal_encoder = make_column_transformer(
    (
        OrdinalEncoder(handle_unknown="use_encoded_value", unknown_value=np.nan),
        make_column_selector(dtype_include="category"),
    ),
    remainder="passthrough",
)

hist_ordinal = make_pipeline(
    ordinal_encoder, HistGradientBoostingRegressor(random_state=42)
)
hist_ordinal

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('ordinalencoder',
                                                  OrdinalEncoder(handle_unknown='use_encoded_value',
                                                                 unknown_value=nan),
                                                  <sklearn.compose._column_transformer.make_column_selector object at 0x7fb4a1b6f790>)])),
                ('histgradientboostingregressor',
                 HistGradientBoostingRegressor(random_state=42))])

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Gradient Boosting Schätzer mit Target-Kodierung#

Eine weitere Möglichkeit ist die Verwendung des TargetEncoder, der die Kategorien basierend auf dem Mittelwert der (Trainings-)Zielvariable kodiert, wie er mit einem geglätteten np.mean(y, axis=0) berechnet wird, d.h.:

in der Regression wird der Mittelwert von y verwendet;
in der binären Klassifizierung die Rate der positiven Klasse;
in der Multiklassenklassifizierung ein Vektor von Klassenraten (eine pro Klasse).

Für jede Kategorie berechnet er diese Zielmittelwerte mithilfe von Cross Fitting, was bedeutet, dass die Trainingsdaten in Folds aufgeteilt werden: in jedem Fold werden die Mittelwerte nur auf einem Teil der Daten berechnet und dann auf den zurückgehaltenen Teil angewendet. Auf diese Weise wird jede Stichprobe mit Statistiken aus Daten kodiert, zu denen sie nicht gehörte, was Informationslecks aus dem Ziel verhindert.

from sklearn.preprocessing import TargetEncoder

target_encoder = make_column_transformer(
    (
        TargetEncoder(target_type="continuous", random_state=42),
        make_column_selector(dtype_include="category"),
    ),
    remainder="passthrough",
)

hist_target = make_pipeline(
    target_encoder, HistGradientBoostingRegressor(random_state=42)
)
hist_target

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('targetencoder',
                                                  TargetEncoder(random_state=42,
                                                                target_type='continuous'),
                                                  <sklearn.compose._column_transformer.make_column_selector object at 0x7fb4a1b6f2d0>)])),
                ('histgradientboostingregressor',
                 HistGradientBoostingRegressor(random_state=42))])

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Gradient Boosting Schätzer mit nativer kategorialer Unterstützung#

Nun erstellen wir einen HistGradientBoostingRegressor Schätzer, der kategoriale Merkmale nativ ohne explizite Kodierung verarbeiten kann. Diese Funktionalität kann durch Setzen von categorical_features="from_dtype", was automatisch Merkmale mit kategorialen Datentypen erkennt, oder expliziter durch categorical_features=categorical_columns_subset aktiviert werden.

Im Gegensatz zu früheren Kodierungsansätzen behandelt der Schätzer die kategorialen Merkmale nativ. Bei jeder Aufteilung partitioniert er die Kategorien eines solchen Merkmals in disjunkte Mengen, wobei eine Heuristik verwendet wird, die sie nach ihrer Auswirkung auf die Zielvariable sortiert. Siehe Split-Findung mit kategorialen Merkmalen für Details.

Während die ordinale Kodierung bei Merkmalen mit geringer Kardinalität gut funktionieren kann, auch wenn die Kategorien keine natürliche Reihenfolge haben, erfordert das Erreichen sinnvoller Aufteilungen tiefere Bäume, wenn die Kardinalität steigt. Die native kategoriale Unterstützung vermeidet dies, indem sie direkt mit ungeordneten Kategorien arbeitet. Der Vorteil gegenüber der One-Hot-Kodierung liegt in der ausgelassenen Vorverarbeitung und einer schnelleren Trainings- und Vorhersagezeit.

hist_native = HistGradientBoostingRegressor(
    random_state=42, categorical_features="from_dtype"
)
hist_native

HistGradientBoostingRegressor(random_state=42)

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Modellvergleich#

Hier verwenden wir Kreuzvalidierung, um die Modellleistung in Bezug auf mean_absolute_percentage_error und Trainingszeiten zu vergleichen. In den folgenden Diagrammen stellen die Fehlerbalken die 1-fache Standardabweichung dar, wie sie über die Kreuzvalidierung-Splits berechnet wurde.

from sklearn.model_selection import cross_validate

common_params = {"cv": 5, "scoring": "neg_mean_absolute_percentage_error", "n_jobs": -1}

dropped_result = cross_validate(hist_dropped, X, y, **common_params)
one_hot_result = cross_validate(hist_one_hot, X, y, **common_params)
ordinal_result = cross_validate(hist_ordinal, X, y, **common_params)
target_result = cross_validate(hist_target, X, y, **common_params)
native_result = cross_validate(hist_native, X, y, **common_params)
results = [
    ("Dropped", dropped_result),
    ("One Hot", one_hot_result),
    ("Ordinal", ordinal_result),
    ("Target", target_result),
    ("Native", native_result),
]

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker


def plot_performance_tradeoff(results, title):
    fig, ax = plt.subplots()
    markers = ["s", "o", "^", "x", "D"]

    for idx, (name, result) in enumerate(results):
        test_error = -result["test_score"]
        mean_fit_time = np.mean(result["fit_time"])
        mean_score = np.mean(test_error)
        std_fit_time = np.std(result["fit_time"])
        std_score = np.std(test_error)

        ax.scatter(
            result["fit_time"],
            test_error,
            label=name,
            marker=markers[idx],
        )
        ax.scatter(
            mean_fit_time,
            mean_score,
            color="k",
            marker=markers[idx],
        )
        ax.errorbar(
            x=mean_fit_time,
            y=mean_score,
            yerr=std_score,
            c="k",
            capsize=2,
        )
        ax.errorbar(
            x=mean_fit_time,
            y=mean_score,
            xerr=std_fit_time,
            c="k",
            capsize=2,
        )

    ax.set_xscale("log")

    nticks = 7
    x0, x1 = np.log10(ax.get_xlim())
    ticks = np.logspace(x0, x1, nticks)
    ax.set_xticks(ticks)
    ax.xaxis.set_major_formatter(ticker.FormatStrFormatter("%1.1e"))
    ax.minorticks_off()

    ax.annotate(
        "  best\nmodels",
        xy=(0.04, 0.04),
        xycoords="axes fraction",
        xytext=(0.09, 0.14),
        textcoords="axes fraction",
        arrowprops=dict(arrowstyle="->", lw=1.5),
    )
    ax.set_xlabel("Time to fit (seconds)")
    ax.set_ylabel("Mean Absolute Percentage Error")
    ax.set_title(title)
    ax.legend()
    plt.show()


plot_performance_tradeoff(results, "Gradient Boosting on Ames Housing")

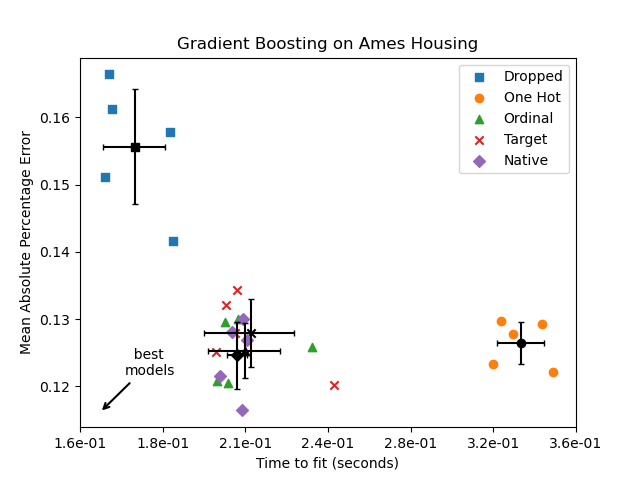
Im obigen Diagramm sind die „besten Modelle“ diejenigen, die sich näher an der unteren linken Ecke befinden, wie durch den Pfeil angezeigt. Diese Modelle würden tatsächlich schnelleres Training und geringere Fehler aufweisen.

Das Modell, das One-Hot-kodierte Daten verwendet, ist das langsamste. Dies ist zu erwarten, da die One-Hot-Kodierung eine zusätzliche Merkmalsspalte für jeden Kategorie-Wert jedes kategorialen Merkmals erstellt, was die Anzahl der Split-Kandidaten während des Trainings erheblich erhöht. Theoretisch erwarten wir, dass die native Verarbeitung kategorialer Merkmale geringfügig langsamer ist als die Behandlung von Kategorien als geordnete Mengen („Ordinal“), da die native Verarbeitung das Sortieren von Kategorien erfordert. Die Trainingszeiten sollten jedoch bei einer kleinen Anzahl von Kategorien nahe beieinander liegen, und dies spiegelt sich möglicherweise nicht immer in der Praxis wider.

Die Zeit, die für das Training mit dem TargetEncoder benötigt wird, hängt vom Parameter cv für Cross Fitting ab, da das Hinzufügen von Splits mit einem Rechenaufwand verbunden ist.

Hinsichtlich der Vorhersageleistung führt das Entfernen der kategorialen Merkmale zur schlechtesten Leistung. Die vier Modelle, die kategoriale Merkmale verwenden, haben vergleichbare Fehlerraten, wobei die native Verarbeitung einen leichten Vorteil hat.

Begrenzung der Anzahl von Splits#

Im Allgemeinen kann man schlechtere Vorhersagen von One-Hot-kodierten Daten erwarten, insbesondere wenn die Baumtiefe oder die Anzahl der Knoten begrenzt sind: Mit One-Hot-kodierten Daten benötigt man mehr Split-Punkte, d.h. mehr Tiefe, um einen äquivalenten Split wiederherzustellen, der mit nativen Mitteln in einem einzigen Split-Punkt erzielt werden könnte.

Dies gilt auch, wenn Kategorien als ordinale Mengen behandelt werden: Wenn die Kategorien A..F sind und der beste Split ACF - BDE ist, würde das One-Hot-Encoder-Modell 3 Split-Punkte benötigen (einen pro Kategorie im linken Knoten), und das ordinale Nicht-Native-Modell würde 4 Splits benötigen: 1 Split, um A zu isolieren, 1 Split, um F zu isolieren, und 2 Splits, um C von BCDE zu isolieren.

Wie stark sich die Leistungen der Modelle in der Praxis unterscheiden, hängt vom Datensatz und der Flexibilität der Bäume ab.

Um dies zu sehen, führen wir die gleiche Analyse mit Unter-Fitting-Modellen erneut durch, bei denen wir die Gesamtzahl der Splits künstlich begrenzen, indem wir sowohl die Anzahl der Bäume als auch die Tiefe jedes Baumes begrenzen.

for pipe in (hist_dropped, hist_one_hot, hist_ordinal, hist_target, hist_native):
    if pipe is hist_native:
        # The native model does not use a pipeline so, we can set the parameters
        # directly.
        pipe.set_params(max_depth=3, max_iter=15)
    else:
        pipe.set_params(
            histgradientboostingregressor__max_depth=3,
            histgradientboostingregressor__max_iter=15,
        )

dropped_result = cross_validate(hist_dropped, X, y, **common_params)
one_hot_result = cross_validate(hist_one_hot, X, y, **common_params)
ordinal_result = cross_validate(hist_ordinal, X, y, **common_params)
target_result = cross_validate(hist_target, X, y, **common_params)
native_result = cross_validate(hist_native, X, y, **common_params)
results_underfit = [
    ("Dropped", dropped_result),
    ("One Hot", one_hot_result),
    ("Ordinal", ordinal_result),
    ("Target", target_result),
    ("Native", native_result),
]

plot_performance_tradeoff(
    results_underfit, "Gradient Boosting on Ames Housing (few and shallow trees)"
)

Gradient Boosting on Ames Housing (few and shallow trees)

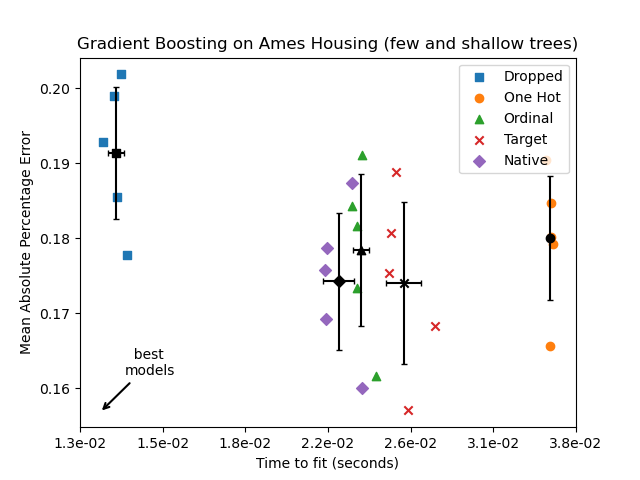
Die Ergebnisse für diese Unter-Fitting-Modelle bestätigen unsere bisherige Intuition: Die native kategoriale Handhabungsstrategie erzielt die besten Ergebnisse, wenn das Budget für Splits begrenzt ist. Die drei expliziten Kodierungsstrategien (One-Hot, Ordinal und Target-Kodierung) führen zu etwas größeren Fehlern als der Schätzer, der kategoriale Merkmale einfach ganz entfernt, aber immer noch besser als das Basismodell.

Gesamte Laufzeit des Skripts: (0 Minuten 4,379 Sekunden)

Verwandte Beispiele

Vergleich von Target Encoder mit anderen Encodern

Column Transformer mit gemischten Typen

Zeitbezogene Merkmalskonstruktion

Prädiktoren mit Stacking kombinieren

Galerie generiert von Sphinx-Gallery

	steps steps: list of tuples Liste von Tupeln (Name des Schritts, Schätzer), die in sequenzieller Reihenfolge verkettet werden sollen. Um mit der scikit-learn API kompatibel zu sein, müssen alle Schritte `fit` definieren. Alle nicht letzten Schritte müssen auch `transform` definieren. Siehe :ref:`Kombination von Schätzern ` für weitere Details.	[('columntransformer', ...), ('histgradientboostingregressor', ...)]
	transform_input transform_input: list of str, default=None Die Namen der :term:`Metadaten`-Parameter, die von der Pipeline transformiert werden sollen, bevor sie an den Schritt übergeben werden, der sie benötigt. Dies ermöglicht die Transformation einiger Eingabeparameter zu ``fit`` (außer ``X``), die von den Schritten der Pipeline bis zu dem Schritt transformiert werden, der sie benötigt. Die Anforderung wird über :ref:`Metadaten-Routing ` definiert. Dies kann beispielsweise verwendet werden, um einen Validierungsdatensatz durch die Pipeline zu leiten. Sie können dies nur festlegen, wenn das Metadaten-Routing aktiviert ist, was Sie mit ``sklearn.set_config(enable_metadata_routing=True)`` aktivieren können. .. versionadded:: 1.6	None
	memory memory: str oder Objekt mit der joblib.Memory-Schnittstelle, default=None Wird zum Zwischenspeichern der angepassten Transformer der Pipeline verwendet. Der letzte Schritt wird niemals zwischengespeichert, auch wenn es sich um einen Transformer handelt. Standardmäßig erfolgt keine Zwischenspeicherung. Wenn ein String angegeben wird, ist dies der Pfad zum Zwischenspeicherverzeichnis. Durch Aktivieren der Zwischenspeicherung wird eine Kopie der Transformer vor dem Anpassen ausgelöst. Daher kann die an die Pipeline übergebene Transformer-Instanz nicht direkt inspiziert werden. Verwenden Sie das Attribut `named_steps` oder `steps`, um Schätzer innerhalb der Pipeline zu inspizieren. Das Zwischenspeichern der Transformer ist vorteilhaft, wenn das Anpassen zeitaufwändig ist. Siehe :ref:`sphx_glr_auto_examples_neighbors_plot_caching_nearest_neighbors.py` für ein Beispiel zur Aktivierung der Zwischenspeicherung.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Schritts gedruckt, wenn es abgeschlossen ist.	False

	transformers transformers: Liste von Tupeln Liste von (Name, Transformer, Spalten)-Tupeln, die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden sollen. name : str Wie in Pipeline und FeatureUnion ermöglicht dies, den Transformer und seine Parameter mit ``set_params`` festzulegen und in der Gitter-Suche zu finden. transformer : {'drop', 'passthrough'} oder Schätzer Schätzer muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten entfernt oder unverändert durchgereicht werden sollen, bzw. 'passthrough'. columns : str, array-ähnlich von str, int, array-ähnlich von int, array-ähnlich von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganzzahlen werden als Positionsspalten interpretiert, während Zeichenketten auf DataFrame-Spalten nach Namen verweisen können. Eine skalare Zeichenkette oder Ganzzahl sollte verwendet werden, wo ``transformer`` erwartet, dass X eine 1D-Array-ähnliche (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein Callable erhält die Eingabedaten `X` und kann jede der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('drop', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'passthrough'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, werden die Namen der Ausgabemerkmale von :meth:`ColumnTransformer.get_feature_names_out` allen Merkmalnamen mit dem Namen des Transformers vorangestellt, der dieses Merkmal generiert hat. Dies entspricht dem Setzen von `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Merkmalnamen voranstellen und einen Fehler ausgeben, wenn die Merkmalnamen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, werden alle Merkmale mit dem Namen des Transformers umbenannt, indem :meth:`ColumnTransformer.get_feature_names_out` verwendet wird. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Merkmalname. Die zurückgegebene Zeichenkette wird der neue Merkmalname sein. - Wenn ``str``, muss es eine Zeichenkette sein, die für die Formatierung bereit ist. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe :meth:`str.format` Methode aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein Callable oder eine zu formatierende Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	loss loss: {'squared_error', 'absolute_error', 'gamma', 'poisson', 'quantile'}, default='squared_error' Die Verlustfunktion, die im Boosting-Prozess verwendet wird. Beachten Sie, dass die "squared error", "gamma" und "poisson" Verluste tatsächlich "half least squares loss", "half gamma deviance" und "half poisson deviance" implementieren, um die Berechnung des Gradienten zu vereinfachen. Darüber hinaus verwenden die Verluste "gamma" und "poisson" intern einen Log-Link, "gamma" erfordert ``y > 0`` und "poisson" erfordert ``y >= 0``. "quantile" verwendet den Pinball-Verlust. .. versionchanged:: 0.23 Option 'poisson' hinzugefügt. .. versionchanged:: 1.1 Option 'quantile' hinzugefügt. .. versionchanged:: 1.3 Option 'gamma' hinzugefügt.	'squared_error'
	quantile quantile: float, default=None Wenn loss "quantile" ist, gibt dieser Parameter an, welches Quantil geschätzt werden soll, und muss zwischen 0 und 1 liegen.	None
	learning_rate learning_rate: float, default=0.1 Die Lernrate, auch bekannt als Shrinkage. Sie wird als multiplikativer Faktor für die Blattwerte verwendet. Verwenden Sie ``1`` für keine Schrumpfung.	0.1
	max_iter max_iter: int, default=100 Die maximale Anzahl von Iterationen des Boosting-Prozesses, d.h. die maximale Anzahl von Bäumen.	100
	max_leaf_nodes max_leaf_nodes: int oder None, default=31 Die maximale Anzahl von Blättern pro Baum. Muss strikt größer als 1 sein. Wenn None, gibt es keine maximale Grenze.	31
	max_depth max_depth: int oder None, default=None Die maximale Tiefe jedes Baumes. Die Tiefe eines Baumes ist die Anzahl der Kanten, die vom Wurzelknoten zum tiefsten Blatt führen. Die Tiefe ist standardmäßig nicht begrenzt.	None
	min_samples_leaf min_samples_leaf: int, default=20 Die Mindestanzahl von Samples pro Blatt. Bei kleinen Datensätzen mit weniger als einigen hundert Samples wird empfohlen, diesen Wert zu senken, da nur sehr flache Bäume gebaut würden.	20
	l2_regularization l2_regularization: float, default=0 Der L2-Regularisierungsparameter, der Blätter mit kleinen Hessianen bestraft. Verwenden Sie ``0`` für keine Regularisierung (Standard).	0.0
	max_features max_features: float, default=1.0 Anteil zufällig ausgewählter Merkmale in jedem Knoten-Split. Dies ist eine Form der Regularisierung, kleinere Werte machen die Bäume zu schwächeren Lernern und können Überanpassung verhindern. Wenn Interaktionsbeschränkungen aus `interaction_cst` vorhanden sind, werden nur erlaubte Merkmale für die Unterstichprobe berücksichtigt. .. versionadded:: 1.4	1.0
	max_bins max_bins: int, default=255 Die maximale Anzahl von Bins, die für nicht fehlende Werte verwendet werden sollen. Vor dem Training wird jedes Merkmal des Eingabearrays `X` in ganzzahlige Bins eingeteilt, was eine viel schnellere Trainingsphase ermöglicht. Merkmale mit einer kleinen Anzahl von eindeutigen Werten verwenden möglicherweise weniger als ``max_bins`` Bins. Zusätzlich zu den ``max_bins`` Bins ist immer ein weiterer Bin für fehlende Werte reserviert. Muss nicht größer als 255 sein.	255
	categorical_features categorical_features: array-ähnlich von {bool, int, str} der Form (n_features) oder (n_categorical_features,), Standardwert='from_dtype' Zeigt kategoriale Merkmale an. - None : kein Merkmal wird als kategorial betrachtet. - boolean array-ähnlich : boolean Maske, die kategoriale Merkmale anzeigt. - integer array-ähnlich : integer Indizes, die kategoriale Merkmale anzeigen. - str array-ähnlich: Namen von kategorialen Merkmalen (unter der Annahme, dass die Trainingsdaten Merkmalnamen haben). - `"from_dtype"`: DataFrame-Spalten mit dtype "category" werden als kategoriale Merkmale betrachtet. Die Eingabe muss ein Objekt sein, das eine ``__dataframe__`` Methode exponiert, wie z.B. Pandas oder Polars DataFrames, um diese Funktion zu nutzen. Für jedes kategoriale Merkmal muss es höchstens `max_bins` eindeutige Kategorien geben. Negative Werte für kategoriale Merkmale, die als numerische Datentypen kodiert sind, werden als fehlende Werte behandelt. Alle kategorialen Werte werden in Gleitkommazahlen umgewandelt. Das bedeutet, dass kategoriale Werte von 1.0 und 1 als dieselbe Kategorie behandelt werden. Lesen Sie mehr im :ref:`Benutzerhandbuch ` und :ref:`sphx_glr_auto_examples_ensemble_plot_gradient_boosting_categorical.py`. .. versionadded:: 0.24 .. versionchanged:: 1.2 Unterstützung für Merkmalnamen hinzugefügt. .. versionchanged:: 1.4 Option `"from_dtype"` hinzugefügt. .. versionchanged:: 1.6 Der Standardwert hat sich von `None` auf `"from_dtype"` geändert.	'from_dtype'
	monotonic_cst monotonic_cst: array-ähnlich von int mit shape (n_features) oder dict, default=None Monotone Einschränkungen, die für jedes Merkmal durchgesetzt werden sollen, werden mit den folgenden Integer-Werten angegeben: - 1: monoton steigend - 0: keine Einschränkung - -1: monoton fallend Wenn ein Dict mit String-Schlüsseln, ordnet es Merkmale zu monotonen Einschränkungen nach Namen zu. Wenn ein Array, werden die Merkmale Einschränkungen nach Position zugeordnet. Siehe :ref:`monotonic_cst_features_names` für ein Anwendungsbeispiel. Weiterlesen im :ref:`Benutzerhandbuch `. .. versionadded:: 0.23 .. versionchanged:: 1.2 Akzeptiert Dict von Einschränkungen mit Merkmalnamen als Schlüssel.	None
	interaction_cst interaction_cst: {"pairwise", "no_interactions"} oder Sequenz von Listen/Tupeln/Sets von ints, Standardwert=None Spezifiziert Interaktionsbeschränkungen, die Mengen von Merkmalen, die miteinander in Kindknotenaufteilungen interagieren können. Jedes Element spezifiziert die Menge der Merkmalindizes, die miteinander interagieren dürfen. Wenn es mehr Merkmale gibt als in diesen Beschränkungen angegeben, werden sie so behandelt, als wären sie als zusätzliche Menge angegeben. Die Zeichenketten "pairwise" und "no_interactions" sind Kurzformen für die Erlaubnis nur paarweiser oder gar keiner Interaktionen. Zum Beispiel, mit insgesamt 5 Merkmalen, ist `interaction_cst=[{0, 1}]` äquivalent zu `interaction_cst=[{0, 1}, {2, 3, 4}]`, und spezifiziert, dass jeder Zweig eines Baumes entweder nur nach den Merkmalen 0 und 1 aufteilt oder nur nach den Merkmalen 2, 3 und 4. Siehe :ref:`dieses Beispiel`, wie `interaction_cst` verwendet wird. .. versionadded:: 1.2	None
	warm_start warm_start: bool, default=False Wenn ``True`` gesetzt, wird die Lösung des vorherigen fit-Aufrufs wiederverwendet und weitere Schätzer zum Ensemble hinzugefügt. Damit die Ergebnisse gültig sind, sollte der Schätzer nur auf denselben Daten neu trainiert werden. Siehe :term:`Glossar `.	False
	early_stopping early_stopping: 'auto' oder bool, default='auto' Wenn 'auto', ist Early Stopping aktiviert, wenn die Stichprobengröße größer als 10000 ist oder wenn `X_val` und `y_val` an `fit` übergeben werden. Wenn True, ist Early Stopping aktiviert, andernfalls ist Early Stopping deaktiviert. .. versionadded:: 0.23	'auto'
	scoring scoring: str oder callable oder None, default='loss' Scoring-Methode, die für Early Stopping verwendet wird. Wird nur verwendet, wenn `early_stopping` aktiviert ist. Optionen: - str: siehe :ref:`scoring_string_names` für Optionen. - callable: ein Scorer-Callable-Objekt (z.B. Funktion) mit der Signatur ``scorer(estimator, X, y)``. Siehe :ref:`scoring_callable` für Details. - `None`: der :ref:`Bestimmtheitskoeffizient ` (:math:`R^2`) wird verwendet. - 'loss': Early Stopping wird im Vergleich zum Verlustwert überprüft.	'loss'
	validation_fraction validation_fraction: int oder float oder None, default=0.1 Anteil (oder absolute Größe) der Trainingsdaten, der als Validierungsdaten für Early Stopping zurückgestellt wird. Wenn None, erfolgt Early Stopping auf den Trainingsdaten. Der Wert wird ignoriert, wenn entweder kein Early Stopping durchgeführt wird (z.B. `early_stopping=False`) oder wenn `X_val` und `y_val` an fit übergeben werden.	0.1
	n_iter_no_change n_iter_no_change: int, default=10 Wird verwendet, um zu bestimmen, wann "Early Stop" erfolgen soll. Der Anpassungsprozess wird gestoppt, wenn keiner der letzten ``n_iter_no_change`` Scores besser ist als der ``n_iter_no_change - 1``-te-letzte, bis zu einer gewissen Toleranz. Nur verwendet, wenn Early Stopping durchgeführt wird.	10
	tol tol: float, default=1e-7 Die absolute Toleranz, die beim Vergleichen von Scores während des Early Stoppings verwendet wird. Je höher die Toleranz, desto wahrscheinlicher ist es, dass ein frühes Stoppen erfolgt: eine höhere Toleranz bedeutet, dass es für nachfolgende Iterationen schwieriger ist, als Verbesserung gegenüber dem Referenz-Score zu gelten.	1e-07
	verbose verbose: int, default=0 Die Ausführlichkeitsstufe. Wenn nicht null, werden einige Informationen über den Anpassungsprozess ausgegeben. ``1`` gibt nur eine Zusammenfassung aus, ``2`` gibt Informationen pro Iteration aus.	0
	random_state random_state: int, RandomState-Instanz oder None, default=None Pseudozufallszahlengenerator zur Steuerung der Unterabtastung im Binning-Prozess und der Trainings-/Validierungsdatensatzaufteilung, wenn Early Stopping aktiviert ist. Geben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe an. Siehe :term:`Glossar `.	42

	steps steps: list of tuples Liste von Tupeln (Name des Schritts, Schätzer), die in sequenzieller Reihenfolge verkettet werden sollen. Um mit der scikit-learn API kompatibel zu sein, müssen alle Schritte `fit` definieren. Alle nicht letzten Schritte müssen auch `transform` definieren. Siehe :ref:`Kombination von Schätzern ` für weitere Details.	[('columntransformer', ...), ('histgradientboostingregressor', ...)]
	transform_input transform_input: list of str, default=None Die Namen der :term:`Metadaten`-Parameter, die von der Pipeline transformiert werden sollen, bevor sie an den Schritt übergeben werden, der sie benötigt. Dies ermöglicht die Transformation einiger Eingabeparameter zu ``fit`` (außer ``X``), die von den Schritten der Pipeline bis zu dem Schritt transformiert werden, der sie benötigt. Die Anforderung wird über :ref:`Metadaten-Routing ` definiert. Dies kann beispielsweise verwendet werden, um einen Validierungsdatensatz durch die Pipeline zu leiten. Sie können dies nur festlegen, wenn das Metadaten-Routing aktiviert ist, was Sie mit ``sklearn.set_config(enable_metadata_routing=True)`` aktivieren können. .. versionadded:: 1.6	None
	memory memory: str oder Objekt mit der joblib.Memory-Schnittstelle, default=None Wird zum Zwischenspeichern der angepassten Transformer der Pipeline verwendet. Der letzte Schritt wird niemals zwischengespeichert, auch wenn es sich um einen Transformer handelt. Standardmäßig erfolgt keine Zwischenspeicherung. Wenn ein String angegeben wird, ist dies der Pfad zum Zwischenspeicherverzeichnis. Durch Aktivieren der Zwischenspeicherung wird eine Kopie der Transformer vor dem Anpassen ausgelöst. Daher kann die an die Pipeline übergebene Transformer-Instanz nicht direkt inspiziert werden. Verwenden Sie das Attribut `named_steps` oder `steps`, um Schätzer innerhalb der Pipeline zu inspizieren. Das Zwischenspeichern der Transformer ist vorteilhaft, wenn das Anpassen zeitaufwändig ist. Siehe :ref:`sphx_glr_auto_examples_neighbors_plot_caching_nearest_neighbors.py` für ein Beispiel zur Aktivierung der Zwischenspeicherung.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Schritts gedruckt, wenn es abgeschlossen ist.	False

	transformers transformers: Liste von Tupeln Liste von (Name, Transformer, Spalten)-Tupeln, die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden sollen. name : str Wie in Pipeline und FeatureUnion ermöglicht dies, den Transformer und seine Parameter mit ``set_params`` festzulegen und in der Gitter-Suche zu finden. transformer : {'drop', 'passthrough'} oder Schätzer Schätzer muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten entfernt oder unverändert durchgereicht werden sollen, bzw. 'passthrough'. columns : str, array-ähnlich von str, int, array-ähnlich von int, array-ähnlich von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganzzahlen werden als Positionsspalten interpretiert, während Zeichenketten auf DataFrame-Spalten nach Namen verweisen können. Eine skalare Zeichenkette oder Ganzzahl sollte verwendet werden, wo ``transformer`` erwartet, dass X eine 1D-Array-ähnliche (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein Callable erhält die Eingabedaten `X` und kann jede der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('onehotencoder', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'passthrough'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, werden die Namen der Ausgabemerkmale von :meth:`ColumnTransformer.get_feature_names_out` allen Merkmalnamen mit dem Namen des Transformers vorangestellt, der dieses Merkmal generiert hat. Dies entspricht dem Setzen von `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Merkmalnamen voranstellen und einen Fehler ausgeben, wenn die Merkmalnamen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, werden alle Merkmale mit dem Namen des Transformers umbenannt, indem :meth:`ColumnTransformer.get_feature_names_out` verwendet wird. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Merkmalname. Die zurückgegebene Zeichenkette wird der neue Merkmalname sein. - Wenn ``str``, muss es eine Zeichenkette sein, die für die Formatierung bereit ist. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe :meth:`str.format` Methode aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein Callable oder eine zu formatierende Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	categories categories: 'auto' oder eine Liste von Arrays, Standard='auto' Kategorien (eindeutige Werte) pro Merkmal: - 'auto': Kategorien automatisch aus den Trainingsdaten ermitteln. - Liste: ``categories[i]`` enthält die erwarteten Kategorien in der i-ten Spalte. Die übergebenen Kategorien sollten keine Strings und numerischen Werte innerhalb eines Merkmals mischen und sollten bei numerischen Werten sortiert sein. Die verwendeten Kategorien finden Sie im Attribut ``categories_``. .. versionadded:: 0.20	'auto'
	drop drop: {'first', 'if_binary'} oder ein array-ähnliches Objekt der Form (n_features,), Standardwert=None Spezifiziert eine Methodik zur Entfernung einer der Kategorien pro Merkmal. Dies ist nützlich in Situationen, in denen perfekt kollineare Merkmale Probleme verursachen, wie z.B. beim Einspeisen der resultierenden Daten in ein unregularisiertes lineares Regressionsmodell. Das Entfernen einer Kategorie bricht jedoch die Symmetrie der ursprünglichen Darstellung und kann daher einen Bias in nachfolgenden Modellen induzieren, z.B. für straffreie lineare Klassifikations- oder Regressionsmodelle. - None : alle Merkmale beibehalten (Standard). - 'first' : die erste Kategorie in jedem Merkmal entfernen. Wenn nur eine Kategorie vorhanden ist, wird das Merkmal vollständig entfernt. - 'if_binary' : die erste Kategorie in jedem Merkmal mit zwei Kategorien entfernen. Merkmale mit 1 oder mehr als 2 Kategorien bleiben unverändert. - array : ``drop[i]`` ist die Kategorie im Merkmal ``X[:, i]``, die entfernt werden soll. Wenn `max_categories` oder `min_frequency` zur Gruppierung seltener Kategorien konfiguriert sind, wird das Drop-Verhalten nach der Gruppierung behandelt. .. versionadded:: 0.21 Der Parameter `drop` wurde in 0.21 hinzugefügt. .. versionchanged:: 0.23 Die Option `drop='if_binary'` wurde in 0.23 hinzugefügt. .. versionchanged:: 1.1 Unterstützung für das Entfernen seltener Kategorien.	None
	sparse_output sparse_output: bool, Standard=True Wenn ``True``, wird eine :class:`scipy.sparse.csr_matrix` zurückgegeben, d. h. eine spärliche Matrix im "Compressed Sparse Row" (CSR)-Format. .. versionadded:: 1.2 `sparse` wurde in `sparse_output` umbenannt.	False
	dtype dtype: numerischer Typ, default=np.float64 Gewünschter dtype der Ausgabe.	<class 'numpy.float64'>
	handle_unknown handle_unknown: {'error', 'ignore', 'infrequent_if_exist', 'warn'}, Standardwert='error' Spezifiziert die Art und Weise, wie unbekannte Kategorien während :meth:`transform` behandelt werden. - 'error' : Fehler auslösen, wenn während der Transformation eine unbekannte Kategorie vorhanden ist. - 'ignore' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, sind die resultierenden One-Hot-kodierten Spalten für dieses Merkmal alle Nullen. Bei der inversen Transformation wird eine unbekannte Kategorie als None gekennzeichnet. - 'infrequent_if_exist' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, werden die resultierenden One-Hot-kodierten Spalten für dieses Merkmal auf die seltene Kategorie abgebildet, falls diese existiert. Die seltene Kategorie wird an die letzte Position in der Kodierung abgebildet. Während der inversen Transformation wird eine unbekannte Kategorie auf die Kategorie abgebildet, die als `'infrequent'` gekennzeichnet ist, falls sie existiert. Wenn die Kategorie `'infrequent'` nicht existiert, dann behandelt :meth:`transform` und :meth:`inverse_transform` eine unbekannte Kategorie wie bei `handle_unknown="ignore"`. Seltene Kategorien existieren basierend auf `min_frequency` und `max_categories`. Mehr dazu im :ref:`Benutzerhandbuch `. - 'warn' : Wenn während der Transformation eine unbekannte Kategorie angetroffen wird, wird eine Warnung ausgegeben, und die Kodierung wird dann wie für `handle_unknown="infrequent_if_exist"` beschrieben fortgesetzt. .. versionchanged:: 1.1 `'infrequent_if_exist'` wurde hinzugefügt, um unbekannte Kategorien und seltene Kategorien automatisch zu behandeln. .. versionadded:: 1.6 Die Option `"warn"` wurde in 1.6 hinzugefügt.	'ignore'
	min_frequency min_frequency: int oder float, Standard=None Gibt die minimale Häufigkeit an, unterhalb derer eine Kategorie als selten betrachtet wird. - Wenn `int`, werden Kategorien mit geringerer Kardinalität als selten betrachtet. - Wenn `float`, werden Kategorien mit geringerer Kardinalität als `min_frequency * n_samples` als selten betrachtet. .. versionadded:: 1.1 Lesen Sie mehr im :ref:`Benutzerhandbuch `.	None
	max_categories max_categories: int, Standard=None Gibt eine Obergrenze für die Anzahl der Ausgabemerkmale pro Eingabe- Merkmal an, wenn seltene Kategorien berücksichtigt werden. Wenn es seltene Kategorien gibt, enthält `max_categories` die Kategorie, die die seltenen Kategorien repräsentiert, zusammen mit den häufigen Kategorien. Wenn `None`, gibt es keine Grenze für die Anzahl der Ausgabemerkmale. .. versionadded:: 1.1 Lesen Sie mehr im :ref:`Benutzerhandbuch `.	None
	feature_name_combiner feature_name_combiner: "concat" oder aufrufbar, Standard="concat" Aufrufbare Funktion mit der Signatur `def callable(input_feature, category)`, die einen String zurückgibt. Dies wird verwendet, um Merkmalsnamen zu erstellen, die von :meth:`get_feature_names_out` zurückgegeben werden. `"concat"` verkettet den kodierten Merkmalnamen und die Kategorie mit `feature + "_" + str(category)`. Z. B. erstellt das Merkmal X mit Werten 1, 6, 7 Merkmalnamen `X_1, X_6, X_7`. .. versionadded:: 1.3	'concat'

	transformers transformers: Liste von Tupeln Liste von (Name, Transformer, Spalten)-Tupeln, die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden sollen. name : str Wie in Pipeline und FeatureUnion ermöglicht dies, den Transformer und seine Parameter mit ``set_params`` festzulegen und in der Gitter-Suche zu finden. transformer : {'drop', 'passthrough'} oder Schätzer Schätzer muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten entfernt oder unverändert durchgereicht werden sollen, bzw. 'passthrough'. columns : str, array-ähnlich von str, int, array-ähnlich von int, array-ähnlich von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganzzahlen werden als Positionsspalten interpretiert, während Zeichenketten auf DataFrame-Spalten nach Namen verweisen können. Eine skalare Zeichenkette oder Ganzzahl sollte verwendet werden, wo ``transformer`` erwartet, dass X eine 1D-Array-ähnliche (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein Callable erhält die Eingabedaten `X` und kann jede der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('ordinalencoder', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'passthrough'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, werden die Namen der Ausgabemerkmale von :meth:`ColumnTransformer.get_feature_names_out` allen Merkmalnamen mit dem Namen des Transformers vorangestellt, der dieses Merkmal generiert hat. Dies entspricht dem Setzen von `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Merkmalnamen voranstellen und einen Fehler ausgeben, wenn die Merkmalnamen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, werden alle Merkmale mit dem Namen des Transformers umbenannt, indem :meth:`ColumnTransformer.get_feature_names_out` verwendet wird. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Merkmalname. Die zurückgegebene Zeichenkette wird der neue Merkmalname sein. - Wenn ``str``, muss es eine Zeichenkette sein, die für die Formatierung bereit ist. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe :meth:`str.format` Methode aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein Callable oder eine zu formatierende Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	transformers transformers: Liste von Tupeln Liste von (Name, Transformer, Spalten)-Tupeln, die die Transformer-Objekte spezifizieren, die auf Teilmengen der Daten angewendet werden sollen. name : str Wie in Pipeline und FeatureUnion ermöglicht dies, den Transformer und seine Parameter mit ``set_params`` festzulegen und in der Gitter-Suche zu finden. transformer : {'drop', 'passthrough'} oder Schätzer Schätzer muss :term:`fit` und :term:`transform` unterstützen. Speziell behandelte Zeichenketten 'drop' und 'passthrough' werden ebenfalls akzeptiert, um anzuzeigen, dass die Spalten entfernt oder unverändert durchgereicht werden sollen, bzw. 'passthrough'. columns : str, array-ähnlich von str, int, array-ähnlich von int, array-ähnlich von bool, slice oder callable Indiziert die Daten auf ihrer zweiten Achse. Ganzzahlen werden als Positionsspalten interpretiert, während Zeichenketten auf DataFrame-Spalten nach Namen verweisen können. Eine skalare Zeichenkette oder Ganzzahl sollte verwendet werden, wo ``transformer`` erwartet, dass X eine 1D-Array-ähnliche (Vektor) ist, andernfalls wird ein 2D-Array an den Transformer übergeben. Ein Callable erhält die Eingabedaten `X` und kann jede der oben genannten zurückgeben. Um mehrere Spalten nach Name oder dtype auszuwählen, können Sie :obj:`make_column_selector` verwenden.	[('targetencoder', ...)]
	remainder remainder: {'drop', 'passthrough'} oder Schätzer, default='drop' Standardmäßig werden nur die in `transformers` spezifizierten Spalten transformiert und im Ergebnis kombiniert, und die nicht spezifizierten Spalten werden verworfen. (Standard von ``'drop'``). Durch Angabe von ``remainder='passthrough'`` werden alle verbleibenden Spalten, die nicht in `transformers` spezifiziert, aber in den an `fit` übergebenen Daten vorhanden waren, automatisch durchgelassen. Diese Teilmenge von Spalten wird mit dem Ergebnis der Transformer verkettet. Für DataFrames werden zusätzliche Spalten, die während `fit` nicht gesehen wurden, aus dem Ergebnis von `transform` ausgeschlossen. Durch Setzen von ``remainder`` auf einen Schätzer verwenden die verbleibenden nicht spezifizierten Spalten den ``remainder``-Schätzer. Der Schätzer muss :term:`fit` und :term:`transform` unterstützen. Beachten Sie, dass die Verwendung dieser Funktion erfordert, dass die DataFrame-Spalten bei `fit` und `transform` die gleiche Reihenfolge haben.	'passthrough'
	sparse_threshold sparse_threshold: float, default=0.3 Wenn die Ausgabe der verschiedenen Transformer dünnbesetzte Matrizen enthält, werden diese als dünnbesetzte Matrix gestapelt, wenn die Gesamtdichte geringer ist als dieser Wert. Verwenden Sie ``sparse_threshold=0``, um immer dicht zu liefern. Wenn die transformierte Ausgabe nur dichte Daten enthält, wird das gestapelte Ergebnis dicht sein, und dieses Schlüsselwort wird ignoriert.	0.3
	n_jobs n_jobs: int, default=None Anzahl der parallel auszuführenden Jobs. ``None`` bedeutet 1, es sei denn, es befindet sich in einem :obj:`joblib.parallel_backend` Kontext. ``-1`` bedeutet, alle Prozessoren zu verwenden. Siehe :term:`Glossar ` für weitere Details.	None
	transformer_weights transformer_weights: dict, default=None Multiplikative Gewichte für Merkmale pro Transformer. Die Ausgabe des Transformers wird mit diesen Gewichten multipliziert. Schlüssel sind Transformer-Namen, Werte die Gewichte.	None
	verbose verbose: bool, default=False Wenn True, wird die verstrichene Zeit während des Anpassens jedes Transformators gedruckt, wenn er abgeschlossen ist.	False
	verbose_feature_names_out verbose_feature_names_out: bool, str oder Callable[[str, str], str], Standardwert=True - Wenn True, werden die Namen der Ausgabemerkmale von :meth:`ColumnTransformer.get_feature_names_out` allen Merkmalnamen mit dem Namen des Transformers vorangestellt, der dieses Merkmal generiert hat. Dies entspricht dem Setzen von `verbose_feature_names_out="{transformer_name}__{feature_name}"`. - Wenn False, wird :meth:`ColumnTransformer.get_feature_names_out` keine Merkmalnamen voranstellen und einen Fehler ausgeben, wenn die Merkmalnamen nicht eindeutig sind. - Wenn ``Callable[[str, str], str]``, werden alle Merkmale mit dem Namen des Transformers umbenannt, indem :meth:`ColumnTransformer.get_feature_names_out` verwendet wird. Das erste Argument des Callables ist der Transformer-Name und das zweite Argument der Merkmalname. Die zurückgegebene Zeichenkette wird der neue Merkmalname sein. - Wenn ``str``, muss es eine Zeichenkette sein, die für die Formatierung bereit ist. Die gegebene Zeichenkette wird mit zwei Feldnamen formatiert: ``transformer_name`` und ``feature_name``. z.B. ``"{feature_name}__{transformer_name}"``. Siehe :meth:`str.format` Methode aus der Standardbibliothek für weitere Informationen. .. versionadded:: 1.0 .. versionchanged:: 1.6 `verbose_feature_names_out` kann ein Callable oder eine zu formatierende Zeichenkette sein.	True
	force_int_remainder_cols force_int_remainder_cols: bool, default=False Dieser Parameter hat keine Auswirkung. .. note:: Wenn Sie nicht auf die Liste der Spalten für die verbleibenden Spalten im ``transformers_`` angepassten Attribut zugreifen, müssen Sie diesen Parameter nicht setzen. .. versionadded:: 1.5 .. versionchanged:: 1.7 Der Standardwert für `force_int_remainder_cols` ändert sich von `True` auf `False` in Version 1.7. .. deprecated:: 1.7 `force_int_remainder_cols` ist veraltet und wird in Version 1.9 entfernt.	'deprecated'

	categories categories: "auto" oder Liste der Form (n_features,) von array-ähnlichen Objekten, Standardwert="auto" Kategorien (eindeutige Werte) pro Merkmal: - `"auto"` : Kategorien werden automatisch aus den Trainingsdaten ermittelt. - list : `categories[i]` enthält die Kategorien, die in der i-ten Spalte erwartet werden. Die übergebenen Kategorien sollten keine Zeichenketten und numerische Werte innerhalb desselben Merkmals mischen und sollten bei numerischen Werten sortiert sein. Die verwendeten Kategorien werden im ``categories_``-Attribut nach dem Training gespeichert.	'auto'
	target_type target_type: {"auto", "continuous", "binary", "multiclass"}, Standardwert="auto" Typ des Ziels. - `"auto"` : Der Typ des Ziels wird mit :func:`~sklearn.utils.multiclass.type_of_target` abgeleitet. - `"continuous"` : Kontinuierliches Ziel - `"binary"` : Binäres Ziel - `"multiclass"` : Multiklassen-Ziel .. note:: Der mit `"auto"` abgeleitete Zieltyp ist möglicherweise nicht der gewünschte Zieltyp, der für die Modellierung verwendet wird. Wenn das Ziel beispielsweise Ganzzahlen zwischen 0 und 100 enthielte, leitet :func:`~sklearn.utils.multiclass.type_of_target` das Ziel als `"multiclass"` ab. In diesem Fall gibt das Setzen von `target_type="continuous"` das Ziel als Regressionsproblem an. Das Attribut `target_type_` gibt den vom Encoder verwendeten Zieltyp an. .. versionchanged:: 1.4 Die Option 'multiclass' wurde hinzugefügt.	'continuous'
	smooth smooth: "auto" oder float, Standardwert="auto" Der Grad der Mischung des Zielmittelwerts, bedingt durch den Wert der Kategorie, mit dem globalen Zielmittelwert. Ein größerer `smooth`-Wert wird mehr Gewicht auf den globalen Zielmittelwert legen. Wenn `"auto"`, dann wird `smooth` auf einen empirischen Bayes-Schätzer gesetzt.	'auto'
	cv cv: int, Standardwert=5 Bestimmt die Anzahl der Folds in der :term:`Cross Fitting`-Strategie, die in :meth:`fit_transform` verwendet wird. Für Klassifikationsziele wird `StratifiedKFold` und für kontinuierliche Ziele `KFold` verwendet.	5
	shuffle shuffle: bool, Standardwert=True Ob die Daten in :meth:`fit_transform` vor der Aufteilung in Folds gemischt werden sollen. Beachten Sie, dass die Stichproben innerhalb jedes Splits nicht gemischt werden.	True
	random_state random_state: int, RandomState-Instanz oder None, Standardwert=None Wenn `shuffle` True ist, beeinflusst `random_state` die Reihenfolge der Indizes, was die Zufälligkeit jedes Folds steuert. Andernfalls hat dieser Parameter keine Auswirkung. Geben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe an. Siehe :term:`Glossar `.	42

Unterstützung kategorialer Merkmale in Gradient Boosting#

Laden des Ames Housing Datensatzes#

Gradient Boosting Schätzer mit entfernten kategorialen Merkmalen#

Gradient Boosting Schätzer mit One-Hot-Kodierung#

Gradient Boosting Schätzer mit ordinaler Kodierung#

Gradient Boosting Schätzer mit Target-Kodierung#

Gradient Boosting Schätzer mit nativer kategorialer Unterstützung#

Modellvergleich#

Begrenzung der Anzahl von Splits#

Diese Seite