Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Rauschpegels von Daten

Dieses Beispiel zeigt die Fähigkeit des WhiteKernel, den Rauschpegel in den Daten zu schätzen. Darüber hinaus zeigen wir die Bedeutung der Initialisierung von Kernel-Hyperparametern.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datengenerierung

Wir arbeiten in einem Setting, in dem X ein einzelnes Merkmal enthält. Wir erstellen eine Funktion, die das zu prognostizierende Ziel generiert. Wir fügen eine Option hinzu, um dem generierten Ziel etwas Rauschen hinzuzufügen.

import numpy as np


def target_generator(X, add_noise=False):
    target = 0.5 + np.sin(3 * X)
    if add_noise:
        rng = np.random.RandomState(1)
        target += rng.normal(0, 0.3, size=target.shape)
    return target.squeeze()

Werfen wir einen Blick auf den Zielgenerator, bei dem wir kein Rauschen hinzufügen, um das Signal zu beobachten, das wir vorhersagen möchten.

X = np.linspace(0, 5, num=80).reshape(-1, 1)
y = target_generator(X, add_noise=False)

import matplotlib.pyplot as plt

plt.plot(X, y, label="Expected signal")
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")

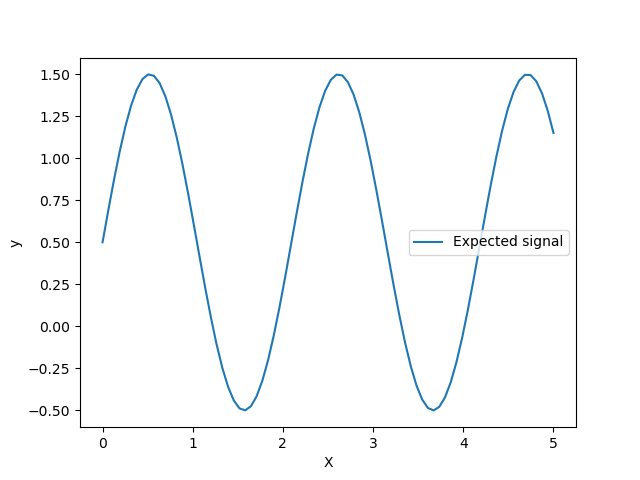
Das Ziel transformiert die Eingabe X mithilfe einer Sinusfunktion. Nun generieren wir einige verrauschte Trainingsstichproben. Um den Rauschpegel zu veranschaulichen, plotten wir das echte Signal zusammen mit den verrauschten Trainingsstichproben.

rng = np.random.RandomState(0)
X_train = rng.uniform(0, 5, size=20).reshape(-1, 1)
y_train = target_generator(X_train, add_noise=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(
    x=X_train[:, 0],
    y=y_train,
    color="black",
    alpha=0.4,
    label="Observations",
)
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")

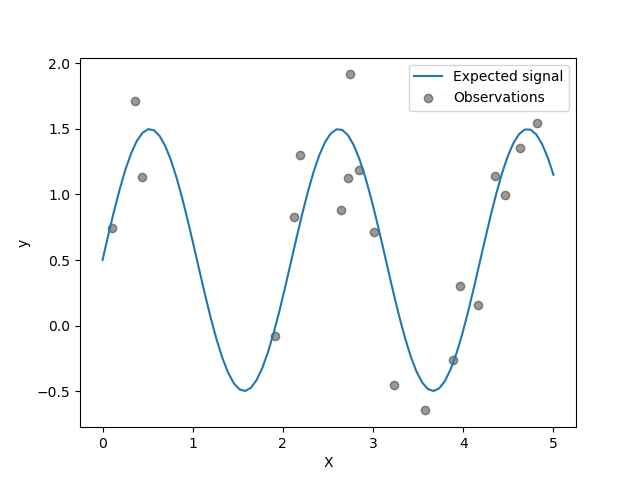
Optimierung von Kernel-Hyperparametern in GPR

Nun erstellen wir einen GaussianProcessRegressor mit einem additiven Kernel, der einen RBF- und einen WhiteKernel-Kernel kombiniert. Der WhiteKernel ist ein Kernel, der die im Datensatz vorhandene Rauschmenge schätzen kann, während der RBF dazu dient, die Nichtlinearität zwischen den Daten und dem Ziel anzupassen.

Wir werden jedoch zeigen, dass der Hyperparameterraum mehrere lokale Minima enthält. Dies unterstreicht die Bedeutung anfänglicher Hyperparameterwerte.

Wir erstellen ein Modell mit einem Kernel, der einen hohen Rauschpegel und eine große Längenskala aufweist, was bedeutet, dass alle Variationen in den Daten durch Rauschen erklärt werden.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel

kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

/home/circleci/project/sklearn/gaussian_process/kernels.py:450: ConvergenceWarning:

The optimal value found for dimension 0 of parameter k1__k2__length_scale is close to the specified upper bound 1000.0. Increasing the bound and calling fit again may find a better value.

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

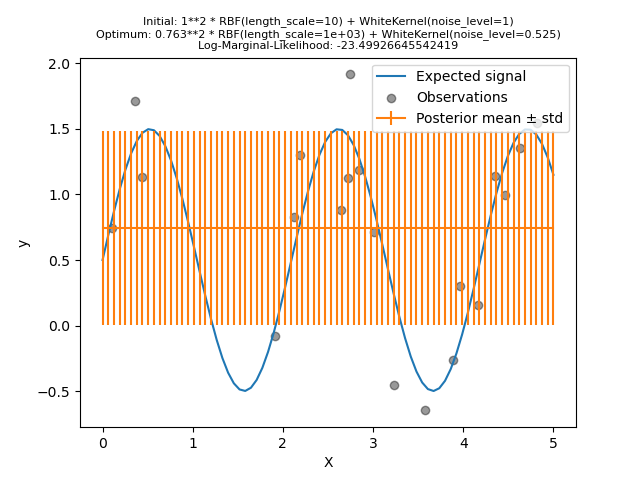
Wir sehen, dass der gefundene optimale Kernel immer noch einen hohen Rauschpegel und eine noch größere Längenskala aufweist. Die Längenskala erreicht die maximal zulässige Grenze für diesen Parameter, und wir erhalten als Ergebnis eine Warnung.

Wichtiger ist, dass wir beobachten, dass das Modell keine nützlichen Vorhersagen liefert: Die mittlere Vorhersage scheint konstant zu sein, sie folgt nicht dem erwarteten rauschfreien Signal.

Nun initialisieren wir den RBF mit einem größeren Anfangswert für die length_scale und den WhiteKernel mit einem kleineren anfänglichen Rauschpegel, während die Parametergrenzen unverändert bleiben.

kernel = 1.0 * RBF(length_scale=1e-1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1e-2, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

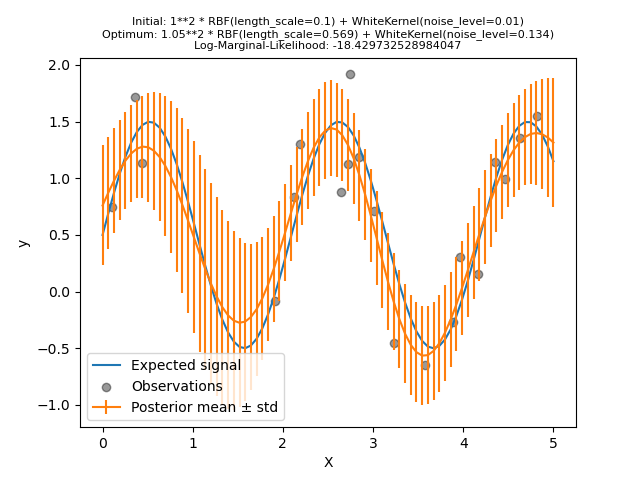
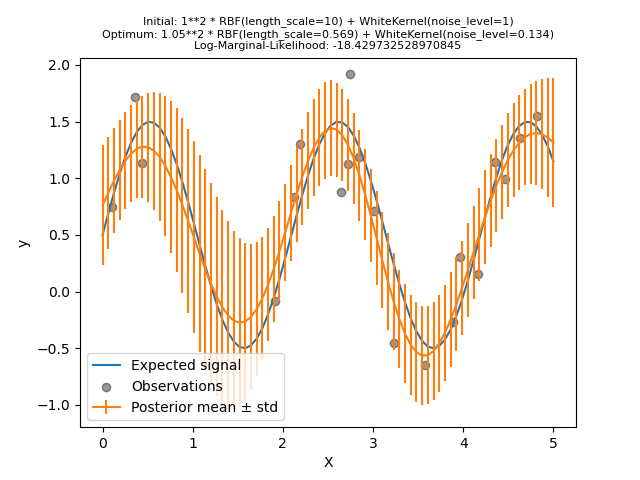
Zuerst sehen wir, dass die Vorhersagen des Modells präziser sind als die des vorherigen Modells: Dieses neue Modell ist in der Lage, die rauschfreie funktionale Beziehung zu schätzen.

Wenn wir uns die Kernel-Hyperparameter ansehen, stellen wir fest, dass die beste gefundene Kombination einen geringeren Rauschpegel und eine kürzere Längenskala als das erste Modell aufweist.

Wir können die negative Log-Marginal-Likelihood (LML) von GaussianProcessRegressor für verschiedene Hyperparameter untersuchen, um ein Gefühl für die lokalen Minima zu bekommen.

from matplotlib.colors import LogNorm

length_scale = np.logspace(-2, 4, num=80)
noise_level = np.logspace(-2, 1, num=80)
length_scale_grid, noise_level_grid = np.meshgrid(length_scale, noise_level)

log_marginal_likelihood = [
    gpr.log_marginal_likelihood(theta=np.log([0.36, scale, noise]))
    for scale, noise in zip(length_scale_grid.ravel(), noise_level_grid.ravel())
]
log_marginal_likelihood = np.reshape(log_marginal_likelihood, noise_level_grid.shape)

vmin, vmax = (-log_marginal_likelihood).min(), 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), num=20), decimals=1)
plt.contour(
    length_scale_grid,
    noise_level_grid,
    -log_marginal_likelihood,
    levels=level,
    norm=LogNorm(vmin=vmin, vmax=vmax),
)
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Length-scale")
plt.ylabel("Noise-level")
plt.title("Negative log-marginal-likelihood")
plt.show()

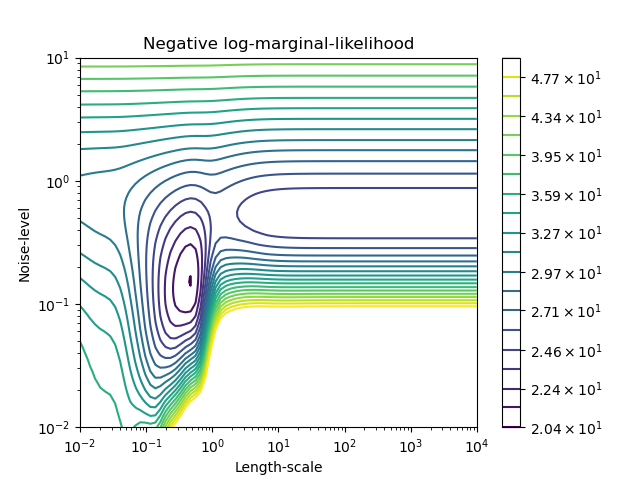
Wir sehen, dass es zwei lokale Minima gibt, die der zuvor gefundenen Kombination von Hyperparametern entsprechen. Abhängig von den Anfangswerten der Hyperparameter konvergiert die gradientenbasierte Optimierung möglicherweise zum besten Modell oder auch nicht. Es ist daher wichtig, die Optimierung mehrmals mit verschiedenen Initialisierungen zu wiederholen. Dies kann durch Setzen des Parameters n_restarts_optimizer der Klasse GaussianProcessRegressor erreicht werden.

Versuchen wir erneut, unser Modell mit den schlechten Anfangswerten anzupassen, diesmal jedoch mit 10 zufälligen Neustarts.

kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(
    kernel=kernel, alpha=0.0, n_restarts_optimizer=10, random_state=0
)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

Wie erhofft, ermöglichen zufällige Neustarts der Optimierung, den besten Satz von Hyperparametern zu finden, trotz der schlechten Anfangswerte.

Verwandte Beispiele

Illustration von Prior und Posterior Gauß-Prozess für verschiedene Kerne

Illustration von Prior und Posterior Gauß-Prozess für verschiedene Kerne

Gauß-Prozesse Regression: grundlegendes Einführungsexempel

Gauß-Prozesse Regression: grundlegendes Einführungsexempel

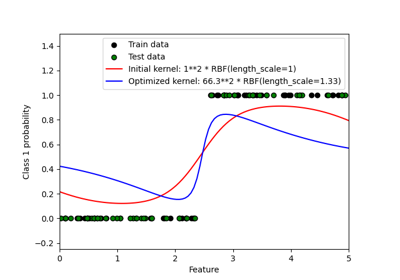
Probabilistische Vorhersagen mit Gauß-Prozess-Klassifikation (GPC)

Probabilistische Vorhersagen mit Gauß-Prozess-Klassifikation (GPC)

Prognose des CO2-Spiegels im Mona Loa Datensatz mittels Gauß-Prozess-Regression (GPR)

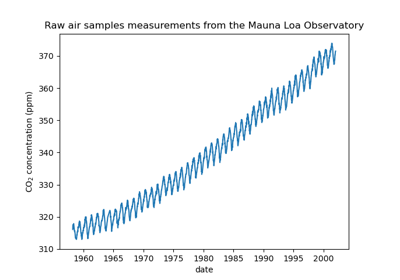
Prognose des CO2-Spiegels im Mona Loa Datensatz mittels Gauß-Prozess-Regression (GPR)