Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Struktur des Entscheidungsbaums verstehen#
Die Struktur des Entscheidungsbaums kann analysiert werden, um weitere Einblicke in die Beziehung zwischen den Merkmalen und dem zu prognostizierenden Ziel zu gewinnen. In diesem Beispiel zeigen wir, wie man Folgendes abruft:
die binäre Baumstruktur;
die Tiefe jedes Knotens und ob er ein Blatt ist oder nicht;
die Knoten, die von einem Sample mit der Methode
decision_patherreicht wurden;das Blatt, das von einem Sample mit der Methode
applyerreicht wurde;die Regeln, die zur Vorhersage eines Samples verwendet wurden;
den Entscheidungspfad, der von einer Gruppe von Samples geteilt wird.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
Trainingsbaumklassifikator#
Zuerst passen wir einen DecisionTreeClassifier mit dem load_iris Datensatz an.
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = DecisionTreeClassifier(max_leaf_nodes=3, random_state=0)
clf.fit(X_train, y_train)
Baumstruktur#
Der Entscheidungs-Klassifikator hat ein Attribut namens tree_, das den Zugriff auf Low-Level-Attribute wie node_count (Gesamtzahl der Knoten) und max_depth (maximale Tiefe des Baums) ermöglicht. Die Methode tree_.compute_node_depths() berechnet die Tiefe jedes Knotens im Baum. tree_ speichert auch die gesamte binäre Baumstruktur, die als eine Reihe von parallelen Arrays dargestellt wird. Das i-te Element jedes Arrays enthält Informationen über den Knoten i. Knoten 0 ist die Wurzel des Baums. Einige der Arrays gelten nur für Blätter oder Teilungsknoten. In diesem Fall sind die Werte der Knoten des anderen Typs beliebig. Zum Beispiel gelten die Arrays feature und threshold nur für Teilungsknoten. Die Werte für Blattknoten in diesen Arrays sind daher beliebig.
Unter diesen Arrays haben wir
children_left[i]: ID des linken Kindes von Knotenioder -1, wenn Blattknotenchildren_right[i]: ID des rechten Kindes von Knotenioder -1, wenn Blattknotenfeature[i]: Merkmal, das zum Teilen von Knoteniverwendet wirdthreshold[i]: Schwellenwert bei Knotenin_node_samples[i]: die Anzahl der Trainingssamples, die Knotenierreichenimpurity[i]: die Unreinheit bei Knoteniweighted_n_node_samples[i]: die gewichtete Anzahl der Trainingssamples, die Knotenierreichenvalue[i, j, k]: die Zusammenfassung der Trainingssamples, die Knoten i für Ausgabe j und Klasse k erreichen (bei Regressionsbäumen ist die Klasse auf 1 gesetzt). Weitere Informationen zuvaluefinden Sie unten.
Mithilfe der Arrays können wir die Baumstruktur durchlaufen, um verschiedene Eigenschaften zu berechnen. Im Folgenden berechnen wir die Tiefe jedes Knotens und ob er ein Blatt ist oder nicht.
n_nodes = clf.tree_.node_count
children_left = clf.tree_.children_left
children_right = clf.tree_.children_right
feature = clf.tree_.feature
threshold = clf.tree_.threshold
values = clf.tree_.value
node_depth = np.zeros(shape=n_nodes, dtype=np.int64)
is_leaves = np.zeros(shape=n_nodes, dtype=bool)
stack = [(0, 0)] # start with the root node id (0) and its depth (0)
while len(stack) > 0:
# `pop` ensures each node is only visited once
node_id, depth = stack.pop()
node_depth[node_id] = depth
# If the left and right child of a node is not the same we have a split
# node
is_split_node = children_left[node_id] != children_right[node_id]
# If a split node, append left and right children and depth to `stack`
# so we can loop through them
if is_split_node:
stack.append((children_left[node_id], depth + 1))
stack.append((children_right[node_id], depth + 1))
else:
is_leaves[node_id] = True
print(
"The binary tree structure has {n} nodes and has "
"the following tree structure:\n".format(n=n_nodes)
)
for i in range(n_nodes):
if is_leaves[i]:
print(
"{space}node={node} is a leaf node with value={value}.".format(
space=node_depth[i] * "\t", node=i, value=np.around(values[i], 3)
)
)
else:
print(
"{space}node={node} is a split node with value={value}: "
"go to node {left} if X[:, {feature}] <= {threshold} "
"else to node {right}.".format(
space=node_depth[i] * "\t",
node=i,
left=children_left[i],
feature=feature[i],
threshold=threshold[i],
right=children_right[i],
value=np.around(values[i], 3),
)
)
The binary tree structure has 5 nodes and has the following tree structure:
node=0 is a split node with value=[[0.33 0.304 0.366]]: go to node 1 if X[:, 3] <= 0.800000011920929 else to node 2.
node=1 is a leaf node with value=[[1. 0. 0.]].
node=2 is a split node with value=[[0. 0.453 0.547]]: go to node 3 if X[:, 2] <= 4.950000047683716 else to node 4.
node=3 is a leaf node with value=[[0. 0.917 0.083]].
node=4 is a leaf node with value=[[0. 0.026 0.974]].
Was ist das hier verwendete Werte-Array?#
Das Array tree_.value ist ein 3D-Array der Form [n_nodes, n_classes, n_outputs], das den Anteil der Samples liefert, die einen Knoten für jede Klasse und jede Ausgabe erreichen. Jeder Knoten hat ein value-Array, das den Anteil der gewichteten Samples darstellt, die diesen Knoten für jede Ausgabe und Klasse im Verhältnis zum Elternknoten erreichen.
Man könnte dies in die absolute gewichtete Anzahl von Samples umwandeln, die einen Knoten erreichen, indem man diese Zahl mit tree_.weighted_n_node_samples[node_idx] für den gegebenen Knoten multipliziert. Beachten Sie, dass in diesem Beispiel keine Sample-Gewichte verwendet werden, sodass die gewichtete Anzahl von Samples gleich der Anzahl der Samples ist, die den Knoten erreichen, da jedes Sample standardmäßig ein Gewicht von 1 hat.
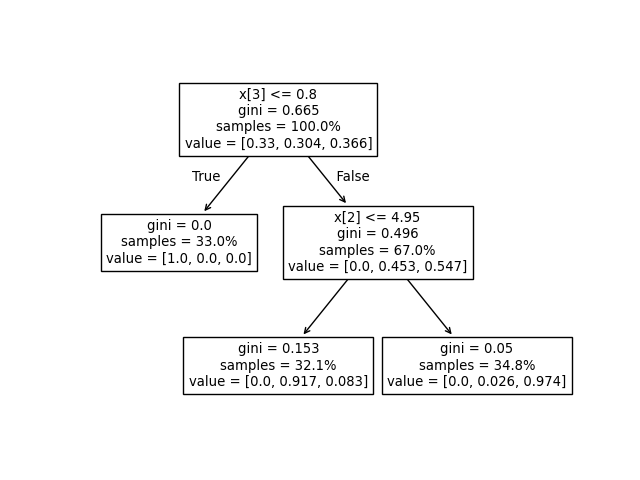
Zum Beispiel hat im obigen Baum, der auf dem Iris-Datensatz basiert, der Wurzelknoten value = [0.33, 0.304, 0.366], was darauf hindeutet, dass 33 % der Samples der Klasse 0, 30,4 % der Klasse 1 und 36,6 % der Klasse 2 am Wurzelknoten vorhanden sind. Man kann dies in die absolute Anzahl der Samples umwandeln, indem man mit der Anzahl der Samples multipliziert, die den Wurzelknoten erreichen, was tree_.weighted_n_node_samples[0] ist. Dann hat der Wurzelknoten value = [37, 34, 41], was bedeutet, dass am Wurzelknoten 37 Samples der Klasse 0, 34 Samples der Klasse 1 und 41 Samples der Klasse 2 vorhanden sind.
Wenn man den Baum durchläuft, werden die Samples aufgeteilt, und infolgedessen ändert sich das value-Array, das jeden Knoten erreicht. Das linke Kind des Wurzelknotens hat value = [1., 0, 0] (oder value = [37, 0, 0], wenn in absolute Sample-Zahlen umgerechnet), da alle 37 Samples im linken Kindknoten aus Klasse 0 stammen.
Hinweis: In diesem Beispiel ist n_outputs=1, aber der Baumklassifikator kann auch Multi-Output-Probleme verarbeiten. Das value-Array an jedem Knoten wäre dann einfach ein 2D-Array.
Wir können die obige Ausgabe mit der Darstellung des Entscheidungsbaums vergleichen. Hier zeigen wir die Proportionen der Samples jeder Klasse, die jeden Knoten erreichen, entsprechend den tatsächlichen Elementen des tree_.value-Arrays.
tree.plot_tree(clf, proportion=True)
plt.show()
Entscheidungspfad#
Wir können auch den Entscheidungspfad von interessierenden Samples abrufen. Die Methode decision_path gibt eine Indikatormatrix aus, mit der wir die Knoten abrufen können, die die interessierenden Samples durchlaufen. Ein Nicht-Null-Element in der Indikatormatrix an Position (i, j) zeigt an, dass das Sample i den Knoten j durchläuft. Oder für ein Sample i bezeichnen die Positionen der Nicht-Null-Elemente in Zeile i der Indikatormatrix die IDs der Knoten, die das Sample durchläuft.
Die von den interessierenden Samples erreichten Blatt-IDs können mit der Methode apply abgerufen werden. Diese gibt ein Array mit den Knoten-IDs der Blätter zurück, die von jedem interessierenden Sample erreicht werden. Unter Verwendung der Blatt-IDs und des decision_path können wir die Teilungsbedingungen erhalten, die zur Vorhersage eines Samples oder einer Gruppe von Samples verwendet wurden. Zuerst tun wir dies für ein einzelnes Sample. Beachten Sie, dass node_index eine sparse Matrix ist.
node_indicator = clf.decision_path(X_test)
leaf_id = clf.apply(X_test)
sample_id = 0
# obtain ids of the nodes `sample_id` goes through, i.e., row `sample_id`
node_index = node_indicator.indices[
node_indicator.indptr[sample_id] : node_indicator.indptr[sample_id + 1]
]
print("Rules used to predict sample {id}:\n".format(id=sample_id))
for node_id in node_index:
# continue to the next node if it is a leaf node
if leaf_id[sample_id] == node_id:
continue
# check if value of the split feature for sample 0 is below threshold
if X_test[sample_id, feature[node_id]] <= threshold[node_id]:
threshold_sign = "<="
else:
threshold_sign = ">"
print(
"decision node {node} : (X_test[{sample}, {feature}] = {value}) "
"{inequality} {threshold})".format(
node=node_id,
sample=sample_id,
feature=feature[node_id],
value=X_test[sample_id, feature[node_id]],
inequality=threshold_sign,
threshold=threshold[node_id],
)
)
Rules used to predict sample 0:
decision node 0 : (X_test[0, 3] = 2.4) > 0.800000011920929)
decision node 2 : (X_test[0, 2] = 5.1) > 4.950000047683716)
Für eine Gruppe von Samples können wir die gemeinsamen Knoten ermitteln, die die Samples durchlaufen.
sample_ids = [0, 1]
# boolean array indicating the nodes both samples go through
common_nodes = node_indicator.toarray()[sample_ids].sum(axis=0) == len(sample_ids)
# obtain node ids using position in array
common_node_id = np.arange(n_nodes)[common_nodes]
print(
"\nThe following samples {samples} share the node(s) {nodes} in the tree.".format(
samples=sample_ids, nodes=common_node_id
)
)
print("This is {prop}% of all nodes.".format(prop=100 * len(common_node_id) / n_nodes))
The following samples [0, 1] share the node(s) [0 2] in the tree.
This is 40.0% of all nodes.
Gesamtlaufzeit des Skripts: (0 Minuten 0,075 Sekunden)
Verwandte Beispiele
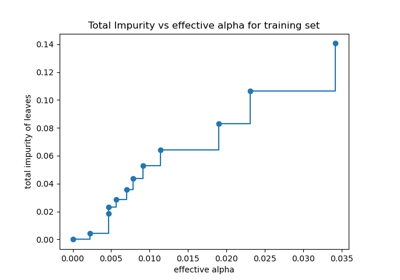
Post-Pruning Entscheidungsbäume mit Kostenkomplexität
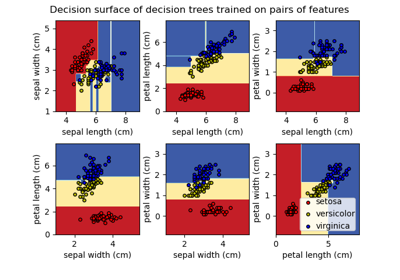
Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten