Vergleich von F-Test und Mutual Information

Dieses Beispiel veranschaulicht die Unterschiede zwischen univariaten F-Test-Statistiken und Mutual Information.

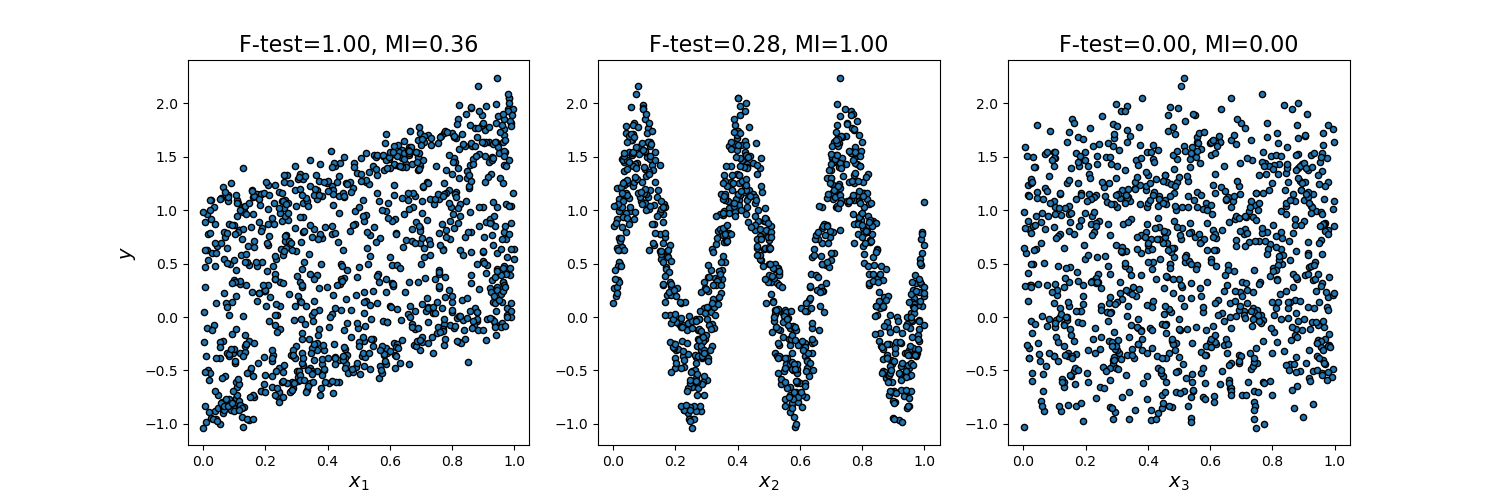
Wir betrachten 3 Merkmale x_1, x_2, x_3, die gleichmäßig über [0, 1] verteilt sind, das Ziel hängt wie folgt davon ab:

y = x_1 + sin(6 * pi * x_2) + 0.1 * N(0, 1), das heißt, das dritte Merkmal ist völlig irrelevant.

Der folgende Code plottet die Abhängigkeit von y gegen einzelne x_i und normalisierte Werte von univariaten F-Test-Statistiken und Mutual Information.

Da der F-Test nur lineare Abhängigkeiten erfasst, stuft er x_1 als das diskriminativste Merkmal ein. Auf der anderen Seite kann Mutual Information jede Art von Abhängigkeit zwischen Variablen erfassen und stuft x_2 als das diskriminativste Merkmal ein, was wahrscheinlich besser mit unserer intuitiven Wahrnehmung für dieses Beispiel übereinstimmt. Beide Methoden kennzeichnen x_3 korrekt als irrelevant.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.feature_selection import f_regression, mutual_info_regression

np.random.seed(0)
X = np.random.rand(1000, 3)
y = X[:, 0] + np.sin(6 * np.pi * X[:, 1]) + 0.1 * np.random.randn(1000)

f_test, _ = f_regression(X, y)
f_test /= np.max(f_test)

mi = mutual_info_regression(X, y)
mi /= np.max(mi)

plt.figure(figsize=(15, 5))
for i in range(3):
    plt.subplot(1, 3, i + 1)
    plt.scatter(X[:, i], y, edgecolor="black", s=20)
    plt.xlabel("$x_{}$".format(i + 1), fontsize=14)
    if i == 0:
        plt.ylabel("$y$", fontsize=14)
    plt.title("F-test={:.2f}, MI={:.2f}".format(f_test[i], mi[i]), fontsize=16)
plt.show()

Verwandte Beispiele

Anpassung für Zufälligkeit in der Clusterleistungsbewertung

Anpassung für Zufälligkeit in der Clusterleistungsbewertung

Testen der Signifikanz eines Klassifikations-Scores mit Permutationen

Testen der Signifikanz eines Klassifikations-Scores mit Permutationen

Univariate Merkmalsauswahl

Univariate Merkmalsauswahl

Vergleich zwischen Gitter-Suche und sukzessiver Halbierung

Vergleich zwischen Gitter-Suche und sukzessiver Halbierung